华师大版备考2023中考数学二轮复习专题15 锐角三角函数

试卷更新日期：2023-01-06 类型：二轮复习

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠C=90°，AB=5，AC=4．下列四个选项，正确的是（）

A、tanB= $\frac{3}{4}$ B、sinB= $\frac{4}{3}$ C、sinB= $\frac{4}{5}$ D、cosB= $\frac{4}{5}$

查看试题解析
2. 已知 $\frac{1}{2}$ <cosA< sin80° ，则锐角A的取值范围是（）

A、60°<A<80° B、30°<A<80° C、10°<A<60° D、10°<A<30°

查看试题解析
3. 若∠A为锐角，且sinA= $\frac{\sqrt{3}}{2}$ ，则cosA等于（）

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 在ΔABC中，∠C＝90°，AC＝8，BC＝6，则tanB的值是（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
5. 如图①，在钝角三角形ABC中，AB＝AC，D为边AB上一动点（B点除外），以CD为一边作正方形CDEF，连结BE，设BD＝ $x$ ， SΔBDE＝ $y$ .若 $y$ 关于 $x$ 的函数图象如图②所示，则sin∠ABC的值为（）

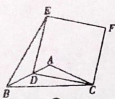
① ②

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{4}$ C、 $\frac{3}{5}$ D、 $\frac{1}{2}$

查看试题解析
6. 如图，以点O为圆心，任意长为半径画弧，与射线 $O A$ 交于点B，再以点B为圆心， $B O$ 长为半径画弧，若两弧交于点C，画射线 $O C$ ，则 $t a n ∠ A O C$ 的值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\sqrt{3}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， D是 $B C$ 的中点，若 $A B = 8$ ， $A D = 5$ ，则 $s i n B$ 等于（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{5}{8}$

查看试题解析
8. 已知在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $s i n A = \frac{\sqrt{3}}{2}$ ，则 $∠ B$ 的度数是（　　）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
9. 如图，在等腰 $△ A B C$ 中， $∠ B A C = 120 °$ ， BC= $6 \sqrt{3}$ ， $⊙ O$ 同时与边 $B A$ 的延长线、射线 $A C$ 相切， $⊙ O$ 的半径为3．将 $△ A B C$ 绕点 $A$ 按顺时针方向旋转 $α (0 ° < α \leq 360 °)$ ， $B$ 、 $C$ 的对应点分别为 $B^{'}$ 、 $C^{'}$ ，在旋转的过程中边 $B^{'} C^{'}$ 所在直线与 $⊙ O$ 相切的次数为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，在等边三角形ABC中，点P，Q分别是AC，BC边上的动点（都不与线段端点重合），且AP=CQ，AQ、BP相交于点O.下列四个结论：①若PC=2AP，则BO=6OP；②若BC=8，BP=7，则PC=5；③AP²=OP⋅AQ；④若AB=3，则OC的最小值为 $\sqrt{3}$ ，其中正确的是（）

A、①③④ B、①②④ C、②③④ D、①②③

查看试题解析

二、填空题

11. 在一张矩形纸片 $A B C D$ 中 $A D = 10$ ， $A B = 4 \sqrt{3}$ ， M，N分别为 $A B$ ， $C D$ 的中点，现将这张纸片按如图所示的方式折叠，使点B落在 $M N$ 上的点F处，则 $E F$ 的长为．

查看试题解析
12. 如图，ΔABC内接于0，AB为0的直径，将ΔABC绕点C旋转到ΔEDC，点E在☉上，已知AE＝2，tanD＝3，则AB＝。

查看试题解析
13. 在 $R t △ A B C$ 中，若 $∠ C = 90 ° ， A C = 4 ， A B = 5$ ，则 $t a n B =$

查看试题解析
14. 在半径为1的圆中，长度等于 $\sqrt{2}$ 的弦所对的圆周角是度

查看试题解析
15. 如图，等边 $△ A B C$ 的边长为2 ，点 $D 、 E 、 F$ 分别是 $B C$ 、 $A B$ 、 $A C$ 边上的中点，以D为圆心， $D E$ 长为半径作 $\overset{⌢}{E F}$ ，连接 $D E 、 D F$ .假设可以在 $△ A B C$ 内部随机取点，那么这个点取在阴影部分的概率是.

查看试题解析

三、解答题

16. 先化简，再求值： $\frac{x - y}{x + 2 y} \div \frac{x^{2} - y^{2}}{x^{2} + 4 x y + 4 y^{2}} - 1$ ，其中 $x = t a n 60 ° + 1$ ， $y = 2 c o s 30 ° - 1$ ．

查看试题解析
17. 先化简，再求值： $(1 - \frac{4}{a + 2}) \div \frac{a^{2} - 4 a + 4}{2 a - 4}$ ，其中 $a = 2^{- 1} + s i n 30 °$ ．

查看试题解析

四、综合题

18. 如图，AB是⊙O的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD＝BD，连接AC交00于点F，连接AE、DE、DF.

(1)、证明：∠E＝∠C；

(2)、若∠E＝55°，求∠BDF的度数；

(3)、设DE交AB于点G，若AB＝10，E是 $\overset{⌢}{AEB}$ 的中点，求EG●ED的值

查看试题解析

华师大版备考2023中考数学二轮复习 专题15 锐角三角函数

一、单选题

二、填空题

三、解答题

四、综合题

华师大版备考2023中考数学二轮复习专题15 锐角三角函数