华师大版备考2023中考数学二轮复习专题13 二次函数一

试卷更新日期：2023-01-06 类型：二轮复习

进入出卷网下载

一、单选题

1. 抛物线 $y = 2 (x - 3)^{2} + 2$ 的顶点坐标是（）

A、 $(- 3 ， 2)$ B、 $(3 ， 2)$ C、 $(- 3 ， - 2)$ D、 $(3 ， - 2)$

查看试题解析
2. 对于二次函数 $y = x^{2} - 4 x - 1$ 的图象，下列说法错误的是（）

A、开口向上 B、与x轴有两个交点 C、抛物线的顶点坐标是（2，－5） D、当x≥2时，y随x的增大而减小

查看试题解析
3. 已知二次函数 $y = {(x - h)}^{2} + 1$ （h为常数），在自变量x的值满足 $1 \leq x \leq 3$ 的情况下，与其对应的函数值y的最小值为 $10$ ，则h的值为（）

A、-2或4 B、0或6 C、1或3 D、-2或6

查看试题解析
4. 二次函数 $y = a x^{2} + b x + c$ 的图象开口向上，对称轴为直线x＝-2，图象经过（1，0），下列结论中，正确的一项（ )

A、 $c > 0$ B、 $4 a c - b^{2} > 0$ C、 $9 a + c > 3 b$ D、 $5 a > b$

查看试题解析
5. 将抛物线 $y = 3 x^{2} + 1$ 向右平移2个单位长度，再向下平移5个单位长度，得到的抛物线的函数表达式为（）

A、 $y = 3 (x + 2)^{2} - 4$ B、 $y = 3 (x - 2)^{2} - 5$ C、 $y = 3 (x - 2)^{2} - 4$ D、 $y = 3 (x + 2)^{2} - 5$

查看试题解析
6. 将抛物线 $y = x^{2}$ 经过下面的平移可得到抛物线 $y = (x + 3)^{2} + 4$ 的是（）

A、向右平移3个单位，向下平移4个单位 B、向右平移3个单位，向上平移4个单位 C、向左平移3个单位，向下平移4个单位 D、向左平移3个单位，向上平移4个单位

查看试题解析
7. 抛物线y＝-x²+bx+3的对称轴为直线x＝-1，若关于x的一元二次方程-x²+bx+3-t＝0（t为实数）在-2＜x＜3的范围内有实数根，则t的取值范围是（）

A、-12＜t≤3 B、-12＜t＜4 C、-12＜t≤4 D、-12＜t＜3

查看试题解析
8. 若点 $A (- 1 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (3 . y_{3})$ 在抛物线 $y = - x^{2} + 4 x + c$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{2} < y_{1}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
9. 如图，已知函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列4个结论：① $a b c > 0$ ；② $a + c < b$ ；③ $4 a + 2 b + c > 0$ ；④ $2 a + b = 0$ ．其中正确结论的有（）

A、①②③ B、②③ C、②③④ D、③④

查看试题解析
10. 如图，抛物线与x轴交于点A，B，与y轴交于点G，正方形 $C D E F$ 的边 $C D$ 在x轴上，E，F在抛物线上，连结 $G A$ ， $G B$ ， $△ A B G$ 是正三角形， $A B = 2$ ，则阴影部分的面积为（）

A、 $\sqrt{3} - \frac{1}{2}$ B、 $3 - \sqrt{3}$ C、 $2 - \frac{\sqrt{2}}{2}$ D、 $2 - \frac{\sqrt{3}}{3}$

查看试题解析

二、填空题

11. 用一段长为 $24 m$ 的篱笆围成一个一边靠墙的矩形养鸡场，若墙长 $10 m$ ，则这个养鸡场最大面积为 $m^{2}$ .

查看试题解析
12. 将抛物线 $y = x^{2}$ 向下平移3个单位长度，再向左平移2个单位长度后，得到的抛物线的解析式为．

查看试题解析
13. 如图，小明以抛物线为灵感，在平面直角坐标系中设计了一款高 $O D$ 为14的奖杯，杯体轴截面 $A B C$ 是抛物线 $y = \frac{4}{9} x^{2} + 5$ 的一部分，则杯口的口径 $A C$ 为.

查看试题解析
14. 已知二次函数y＝x²-2x-2022的图象上有两点A（a，-1）和B（b，-1），则a²+2b-3的值等于 .

查看试题解析
15. 设O为坐标原点，点A、B为抛物线 $y = x^{2}$ 上的两个动点，且 $O A ⊥ O B$ .连接点A、B，过O作 $O C ⊥ A B$ 于点C，则点C到y轴距离的最大值为.

查看试题解析
16. 如图，在平面直角坐标系xOy中，抛物线y＝-x²+6x+c的对称轴与x轴交于点A，在直线AB：y＝kx+3上取一点B，使点B在第四象限，且到两坐标轴的距离和为7，设P是抛物线的对称轴上的一点，点Q在抛物线上，若以点A，B，P，Q为顶点的四边形为正方形，则c的值为．

查看试题解析

三、解答题

17. 已知二次函数的图象顶点为 $P (- 2 ， 2)$ ．且过点为 $A (0 ， - 2)$ ，求该抛物线的解析式．

查看试题解析
18. 某公司研制出一种新颖的家用小电器，每件的生产成本为18元，经市场调研表明，按定价40元出售，每日可销售20件．为了增加销量，每降价1元，日销售量可增加2件．在确保盈利的前提下，当降价多少元时，每天的利润最大?最大利润是多少?

查看试题解析
19. 某农户种植有图1所示蔬菜大棚，其截面示意图如图2所示，其横截面塑料顶棚可以近似看作是抛物线，其中 $O A$ 是地面所在的水平线，点O是塑料顶棚与地面的交点， $A B$ 是保温墙，并且塑料顶棚最高点到点O的水平距离是6米，到地面 $O A$ 的高度是3米．现以 $O A$ 所在直线为x轴，过点O垂直于 $O A$ 的直线为y轴，建立平面直角坐标系．若保温墙 $A B$ 到点O的距离 $O A = 8$ 米．请你求出保温墙AB的高度．

查看试题解析

四、综合题

20. 如图，学校要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园，矩形的一边用教学楼的外墙（外墙足够长），其余三边用竹篱笆围成．其中 $A D \geq A B$ （即长不小于宽），设矩形的宽 $A B$ 的长为x米，矩形 $A B C D$ 面积为y平方米．

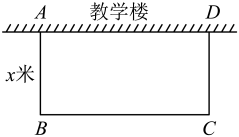(1)、若矩形 $A B C D$ 的面积150平方米，求宽 $A B$ 的长；

(2)、求y与x的函数关系式，并写出自变量x的取值范围；

(3)、矩形地块的宽为多少时，矩形 $A B C D$ 面积最大，并求出最大面积．

查看试题解析

华师大版备考2023中考数学二轮复习 专题13 二次函数一

一、单选题

二、填空题

三、解答题

四、综合题

华师大版备考2023中考数学二轮复习专题13 二次函数一