华师大版备考2023中考数学二轮复习专题11 一次函数

试卷更新日期：2023-01-06 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，一次函数 $y = m x + n$ 的图象与x轴负半轴交于点A，与y轴正半轴交于点B，则下列结论正确的是（）

A、 $m > 0$ ， $n > 0$ B、 $m > 0$ ， $n < 0$ C、 $m < 0$ ， $n > 0$ D、 $m < 0$ ， $n < 0$

查看试题解析
2. 函数y=(k²-1)x+3是一次函数，则k的取值范围是（）

A、k≠1 B、k≠-1 C、k≠±1 D、k为任意实数

查看试题解析
3. 一次函数 $y = k x + 3$ 和正比例函数 $y = k x$ 在同一直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
4. 无论m为何实数，直线y＝-2x+2m与y＝x-4的交点都不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 直线 $y = x - a$ 不经过第二象限，且关于x的方程 $a x^{2} - 2 x + 1 = 0$ 有实数解，则a的取值范围是（）

A、0≤a≤1 B、o≤a<1 C、0<a≤1 D、0<a<1

查看试题解析
6. 如图所示，一次函数 $y = k x + b$ （k，b是常数 $k \neq 0$ ）与正比例函数 $y = m x$ （m是常数， $m \neq 0$ ）的图像相交于点 $M （ 1 ， 2 ）$ ，下列判断错误的是（）

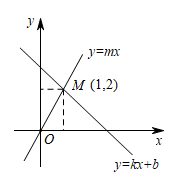A、关于x的方程 $m x = k x + b$ 的解是 $x = 1$ B、关于x的不等式 $m x < k x + b$ 的解集是 $x > 1$ C、当 $x < 0$ 时，函数 $y = k x + b$ 的值比函数 $y = m x$ 的值大 D、关于x，y的方程组 ${\begin{array}{l} y - m x = 0 \\ y - k x - b \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$

查看试题解析
7. 若一次函数 $y = k x - 4$ 的函数值y随x的增大而增大，则k的值可能是（）

A、3 B、-12 C、-4 D、0

查看试题解析
8. 课堂上，同学们研究正比例函数 $y = - x$ 的图象时，得到如下四个结论，其中错误的是（）

A、当 $x = 0$ 时， $y = 0$ ，所以函数 $y = - x$ 的图象经过原点 B、点 $P (t ， - t)$ 一定在函数 $y = - x$ 的图象上 C、当 $x > 0$ 时， $y < 0$ ，当 $x < 0$ 时， $y > 0$ ，所以函数 $y = - x$ 的图象经过二、四象限 D、将函数 $y = - x$ 的图象向左平移2个单位，即可得到函数 $y = - x + 2$ 的图象

查看试题解析
9. 在平面直角坐标系xOy中，已知抛物线 $C_{1} ： y = x^{2} - 1$ ，将 $C_{1}$ 向右平移4个单位，得到抛物线 $C_{2}$ ，过点 $P (p ， 0)$ 作x轴的垂线，交 $C_{1}$ 于点M，交 $C_{2}$ 于点N，q为M与N的纵坐标中的较小值（若二者相等则任取其一），将所有这样的点 $(p ， q)$ 组成的图形记为图形T．若直线y＝x＋n与图形T恰好有4个公共点，则n的取值范围是（）

A、 $- \frac{5}{4} < n < 1$ B、 $- 1 < n < 1$ C、 $- 1 < n \leq 1$ D、 $- 5 < n < 1$

查看试题解析
10. 如图，在平面直角坐标系中，点 $A_{1} ， A_{2} ， A_{3}$ …都在x轴上，点 $B_{1} ， B_{2} ， B_{3}$ ⋯都在直线 $y = x$ 上， $△ O A_{1} B_{1} ， △ B_{1} A_{1} A_{2} ， △ B_{2} B_{1} A_{2} ， △ B_{2} A_{2} A_{3} ， △ B_{3} B_{2} A_{3}$ ⋯都是等腰直角三角形，且 $O A_{1} = 1$ ，则点 $B_{2022}$ 的坐标是（）

A、 $(2^{2020} ， 2^{2020})$ B、 $(2^{2021} ， 2^{2021})$ C、 $(2^{2022} ， 2^{2022})$ D、 $(4042 ， 4042)$

查看试题解析

二、填空题

11. 已知一次函数y＝ax+b，且2a+b＝1，则该一次函数图象必经过点.

查看试题解析
12. 一次函数y＝x+4的图象经过点P（a，b）和Q（c，d），则b（c-d）-a（c-d）的值为

查看试题解析
13. 已知三点 $(1 ， - 1)$ ， $(2 ， - 3)$ ， $(a ， 7)$ 在同一条直线上，则a的值为

查看试题解析
14. 如图，函数y＝2x和y＝ax+2的图象相交于点A（m，4），则不等式2x＜ax+2的解集为.

查看试题解析
15. 如图，一束光线从点O射出，照在经过A（2，0），B（0，2）的镜面上的点D，经AB反射后，反射光线又照到竖立在y轴位置的镜面，经y轴，再反射的光线恰好通过点A，则点D的坐标为.

查看试题解析
16. 如图，点C是直线 $y = - x + 4$ 上的一点，点B是y轴上的动点，当 $O C + B C$ 最小时，点C的坐标为．

查看试题解析
17. 图，直角坐标系 $x O y$ 中，一次函数 $y = - \frac{1}{2} x + 5$ 的图象 $l_{l}$ 分别与x，y轴交于A，B两点，正比例函数的图象 $l_{2}$ 与 $l_{1}$ 交于点 $C (m ， 4)$ ，则m= ，一次函数 $y = k x + 1$ 的图象为 $l_{3}$ ，且 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 不能围成三角形，则k的值为.

查看试题解析

三、解答题

18. 在平面直角坐标系 $x O y$ 中，直线 $y = 2 x + 1$ 与 $x$ 轴交于点A，与y轴交于点B．求点 $A ， B$ 的坐标．

查看试题解析
19. 已知一次函数 $y = (3 m - 8) x + 1 - m$ 的图象与y轴的负半轴相交，y随着x的增大而减小且m为整数，求m的值．

查看试题解析
20. 在平面直角坐标系中，直线 $l_{1}$ ： $y = - \frac{1}{2} x + 4$ 分别与x轴、y轴交于点A、点B，且与直线 $l_{2}$ ： $y = x$ 于点C．
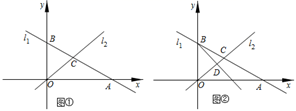
$($ Ⅰ $)$ 如图 $①$ ，求出B、C两点的坐标；

$($ Ⅱ $)$ 若D是线段OC上的点，且 $△ B O D$ 的面积为4，求直线BD的函数解析式．

$($ Ⅲ $)$ 如图 $②$ ，在 $($ Ⅱ $)$ 的条件下，设P是射线BD上的点，在平面内是否存在点Q，使以O、B、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析

四、综合题

21. 已知一次函数 $y_{1} = a x + b$ 的图象交x轴和y轴于点B和D；另一个一次函数 $y_{2} = b x + a$ 的图象交x轴和y轴于点C和E，且两个函数的图象交于点 $A (1 ， 4)$

(1)、当a，b为何值时， $y_{1}$ 和 $y_{2}$ 的图象重合；

(2)、当 $0 < a < 4$ ，且在 $x < 1$ 时，则 $y_{1} > y_{2}$ 成立，求b的取值范围；

(3)、当 $△ A B C$ 的面积为 $\frac{16}{3}$ 时，求线段 $D E$ 的长．

查看试题解析
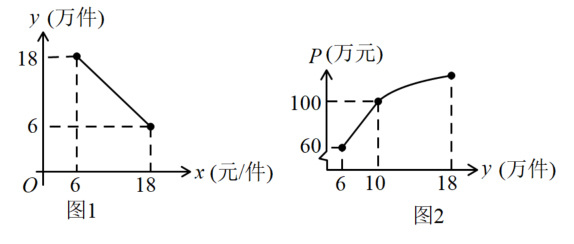22. 嘉兴某公司抓住“一带一路”的机遇不断创新发展，生产销售某产品.该产品销售量y（万件）与售价x（元/件）之间存在图1（一条线段）所示的变化趋势，总成本P（万元）与销售量y（万件）之间存在图2所示的变化趋势，当 $6 \leq y \leq 10$ 时可看成一条线段，当 $10 \leq y \leq 18$ 时可看成抛物线 $P = - \frac{1}{5} y^{2} + 8 y + m$ .

(1)、写出y与x之间的函数关系式；

(2)、若销售量不超过10万件时，利润为45万元.求此时的售价为多少元/件？

(3)、当售价为多少元时，利润最大，最大值是多少万元？（利润＝销售总额－总成本）

查看试题解析

华师大版备考2023中考数学二轮复习 专题11 一次函数

一、单选题

二、填空题

三、解答题

四、综合题

华师大版备考2023中考数学二轮复习专题11 一次函数