华师大版备考2023中考数学二轮复习专题6 二元一次方程

试卷更新日期：2023-01-06 类型：二轮复习

进入出卷网下载

一、单选题

1. 若（m﹣1）x+my＝3是关于x、y的二元一次方程，则m的值不可以是（）

A、﹣1 B、1 C、2 D、3

查看试题解析
2. 关于x，y的二元一次方程3x﹣ay＝1有一组解是 ${\begin{cases} x = 3 \\ y = 4 \end{cases}$ ，则a的值为（）

A、1 B、2 C、3 D、4

查看试题解析
3. 下列方程组是二元一次方程组的是（）

A、 ${\begin{array}{l} m n = 2 \\ m + n = 3 \end{array}$ B、 ${\begin{array}{l} 5 m - 2 n = 0 \\ \frac{1}{m} + n = 3 \end{array}$ C、 ${\begin{array}{l} m + n = 0 \\ 3 m + 2 a = \frac{1}{6} \end{array}$ D、 ${\begin{array}{l} m = 8 \\ \frac{m}{3} - \frac{n}{2} = 1 \end{array}$

查看试题解析
4. “校长杯”青少年校园足球联赛的比赛规则是：胜一场得3分，平一场得1分，负一场得0分．某校足球队在第一轮比赛中赛了7场，以不败的战绩获得 $17$ 分．那么该队胜了几场，平了几场？设该队胜了x场，平了y场，根据题意可列方程组为（）

A、 ${\begin{array}{l} x - y = 7 \\ x + 3 y = 17 \end{array}$ B、 ${\begin{array}{l} x - y = 7 \\ 3 x + y = 17 \end{array}$ C、 ${\begin{array}{l} x + y = 7 \\ x + 3 y = 17 \end{array}$ D、 ${\begin{array}{l} x + y = 7 \\ 3 x + y = 17 \end{array}$

查看试题解析
5. 若关于x，y的二元一次方程组 ${\begin{array}{l} x + 2 y = 2 k \\ 4 x - y = 5 k \end{array}$ 的解满足x-y=1，则k的值是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 用加减法解方程组 ${\begin{cases} 2 x - 5 y = 3 ① \\ 4 x - 2 y = 8 ② . \end{cases}}$ 下列解法不正确的是（）

A、①×2－②，消去x B、①×2－②×5，消去y C、①×(－2)+②，消去x D、①×2－②×(－5)，消去y

查看试题解析
7. 已知二元一次方程组 $\{\begin{cases} x + y = 1 \\ () \end{cases}$ 的解是 ${\begin{cases} x = - 2 \\ y = 3 \end{cases}$ ，则括号内的方程可能是（）

A、y-4x= -5 B、2x-3y=-13 C、y=2x+5 D、x=y-1

查看试题解析
8. 两个形状大小完全相同的长方形中放入4个相同的小长方形后，得到图①和图②的阴影部分，如果大长方形的长为m，则图②与图①的阴影部分周长之差是（）

A、 $- \frac{m}{2}$ B、 $\frac{m}{2}$ C、 $\frac{m}{3}$ D、 $- \frac{m}{3}$

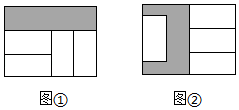查看试题解析
9. 用如图 $①$ 中的长方形和正方形纸板作侧面和底面，做成如图 $②$ 的竖式和横式的两种无盖纸盒.现有 $m$ 张正方形纸板和 $n$ 张长方形纸板，如果做两种纸盒若干个，恰好将纸板用完，则 $m + n$ 的值可能是（）

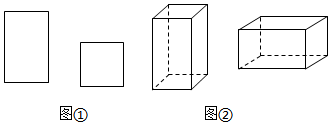A、2019 B、2020 C、2021 D、2022

查看试题解析
10. 已知关于x，y的方程组 ${\begin{matrix} x + 2 y = k \\ 2 x + 3 y = 3 k - 1 \end{matrix}$ ，以下结论：①当k=0时，方程组的解也是方程 $x - 2 y = - 4$ 的解；②存在实数k，使得x+y=0；③不论k取什么实数，x+3y的值始终不变；④若3x+2y=6则k=1.其中正确的是（）

A、①②③ B、①②④ C、①③ D、①②

查看试题解析

二、填空题

11. 已知方程组 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = 5 \end{array}$ ，则x-y的值为．

查看试题解析
12. 已知 $(a - \frac{1}{2})_{}^{2} + | b + 2 | = 0$ ，则 ${(a b)}_{}$ = ．

查看试题解析
13. 用加减消元法解方程组 $\{\begin{cases} 3 a - 2 b = 6 \dots ① \\ 5 a + 3 b = - 2 \dots ② \end{cases}$ 时，把①×3+②×2，得．

查看试题解析
14. 若 $| x - 3 | + {(y + 1)}^{2} = 0$ ，则 $y^{x}$ =。

查看试题解析
15. 已知 $a - b = m$ ，在关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} 2 x - y = - 1 \\ x + 2 y = 5 a - 8 \end{array}$ 中， $x < 0$ ， $y > 0$ ，则 $a$ 的取值范围是， $2 | a + b - 3 + m | - 3 | m - 4 + a + b | =$ .

查看试题解析
16. 已知点O是数轴的原点，点A、B、C在数轴上对应的数分别是﹣12、b、c ，且b、c满足（b﹣9）²+|c﹣15|＝0，动点P从点A出发以2单位/秒的速度向右运动，同时点Q从点C出发，以1个单位/秒速度向左运动，O、B两点之间为“变速区”，规则为从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速，从点B运动到点O期间速度变为原来的3倍，之后立刻恢复原速，运动时间为秒时，P、Q两点到点B的距离相等．

查看试题解析

三、计算题

17. 解方程组：

(1)、 ${\begin{array}{l} y = 2 x ① \\ 2 x + y = 8 ② \end{array}$ ；

(2)、 ${\begin{array}{l} 2 x - 5 y = 7 ① \\ 3 x + 2 y = 1 ② \end{array}$ ．

查看试题解析

四、解答题

18. 一个被墨水污染了的方程组： ${\begin{array}{l} * x + * y = 2 \\ * x - 7 y = 8 \end{array}$ ，小明回忆道：“这个方程组的解是 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ ，而我求的解是 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ ，经检验后发现，我的错误是由于看错了第二个方程中的系数所致”根据小明的回忆，你能求出原方程组吗？

查看试题解析

19. 2022年冬奥会上智慧化全覆盖，机器人得到广泛应用，冬奥会组委会针对不同的物品运送场景选取了几个不同类型的智能物流机器人．这样不仅能高效运输，同时也能减少人员接触．具体运输情况如下表所示：

	A型机器人/个	B型机器人/个	运输物品总数/件
第一批	2	5	34
第二批	4	3	26

问：每个 $A$ 型机器人和 $B$ 型机器人分别可以运输物品多少件？

查看试题解析

20. 某校七年级（1）班、（2）班的同学积极参加全民健身活动，为此两班到同一商店购买体育用品．已知七年级（1）班买了3个篮球和4副羽毛球拍共用了270元；七年级（2）班买了同样的5个篮球和6副羽毛球拍共用了430元；问每个篮球和每副羽毛球拍各多少元？

查看试题解析
21. 疫情防控，人人有责，做好新冠肺炎疫情防控时刻不能放松，因此某校举办“疫情防控”宣传活动，计划购买 $A 、 B$ 两种奖品以鼓励积极参与的学生.经市场调查发现，若购买 $A$ 种1件、 $B$ 种2件，共需24元；若购买 $A$ 种3件、 $B$ 种1件，共需52元. $A 、 B$ 两种奖品每件各多少元?

查看试题解析

五、综合题

22. 某水产养殖户，一次性收购了 $20000$ $k g$ 小龙虾，计划养殖一段时间后再出售.已知每天放养的费用相同，放养 $10$ 天的总成本为 $30.4$ 万元；放养 $20$ 天的总成本为 $30.8$ 万元（总成本=放养总费用+收购成本）.

(1)、设每天的放养费用是a万元，收购成本为b万元，求a和b的值；

(2)、设这批小龙虾放养t天后的质量为m（ $k g$ ），销售单价为y元/ $k g$ .根据以往经验可知：m与t的函数关系式为 $m = {\begin{cases} 20000 (0 \leq t \leq 50) \\ 100 t + 15000 (50 ＜ t \leq 100) \end{cases}$ ， y与t的函数关系如图所示
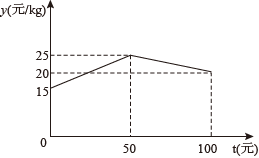
①求y与t的函数关系式；
②设将这批小龙虾放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出W的最大值.（利润=销售总额－总成本）

查看试题解析
23. 【方法感悟】阅读下面材料：
点A，B在数轴上分别表示实数a，b，A，B两点之间的距离表示为 $| A B |$ .如图1，从数轴上看，若点A，B表示的分别是1，4则 $| A B | = | 4 - 1 | = 3$ 或 $| A B | = | 1 - 4 | = 3$ ；

若点A，B表示的数分别是 $- 1$ ， 4则 $| A B | = | 4 - (- 1) | = 4 + 1 = 5$ 或 $| A B | = | - 1 - 4 | = | - 5 | = 5$ ；

若点A，B表示的数分别是 $- 1$ ， $- 4$ ，则 $| A B | = | (- 1) - (- 4) | = | - 1 + 4 | = 3$ 或 $| A B | = | - 4 - (- 1) | = | - 4 + 1 | = 3$ ．

【归纳】若点A，B表示的数分别是 $x_{1}$ ， $x_{2}$ 则 $| A B | = | x_{1} - x_{2} |$ 或 $| A B | = | x_{2} - x_{1} |$ ．

【知识迁移】

(1)、如图1，点A，B表示的数分别是 $- 4.5$ ， b且 $| A B | = 3$ ，则 $b =$ ；

(2)、如图2，点A，B表示的数分别是 $x_{1}$ ， $x_{2}$ ，若把 $A B$ 向左平移 $| A B |$ 个单位，则点A与 $- 50$ 重合，若把 $A B$ 向右平移 $| A B |$ 个单位，则点B与70重合，那么 $x_{1} =$ ， $x_{2} =$ ；

(3)、【拓展应用】
一天，美羊羊去问村长爷爷的年龄，村长爷爷说：“我若是你现在这么大，你还要40年才出生呢，你若是我现在这么大，我已经是老寿星了，116岁了，哈哈！”美羊羊纳闷，请问村长爷爷现在到底是多少岁？美羊羊现在又是几岁？请写出解题思路.

(4)、结合几何意义，求 $| x - 1 | + | x - 2 | + | x - 3 | + | x - 4 | + | x - 5 |$ 最小值.

查看试题解析

华师大版备考2023中考数学二轮复习 专题6 二元一次方程

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

华师大版备考2023中考数学二轮复习专题6 二元一次方程