人教版备考2023中考数学二轮复习 专题33 规律探索问题----数与式
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2n来表示.即:21=2,22=4,23=8,24=16,25=32,……,请你推算22022的个位数字是( )A、8 B、6 C、4 D、22. 在学习“勾股数”的知识时,爱思考的小琪同学发现了一组有规律的勾股数,并将它们记录在如下的表格中,则当a=18时,b+c的值为( )
a
6
8
10
12
14
…
b
8
15
24
35
48
…
c
10
17
26
37
50
…
A、242 B、200 C、188 D、1623. 观察下列代数式: , , , , ….按此规律,则第n个代数式是( )A、 B、 C、 D、4. 按如下的方法构造一个多位数:先任意写一个整数n(0<n<10)作为第一位上的数字,将这个整数n乘以3,若积为一位数,则将其作为第2位上的数字,若积为两位数,则将其个位数字作为第2位上的数字;再将第2位上的数字乘以3,若积为一位数,则将其作为第3位上的数字,若积为两位数,则将其个位数字作为第3位上的数字;…以此类推.若先任意写的一个整数n是7作为第一位上的数字,进行2020次如上操作后得到了第2021位上的数字,则第2022位上的数字是( )A、1 B、3 C、7 D、95. 填在如图各正方形中的四个数之间都有一定的规律,按此规律得出、的值分别为( ) A、 , B、 , C、 , D、 ,6. 定义一种对正整数 的“F”运算: ①当 为奇数时, ; ②当 为偶数时, (其中 是使 为奇数的正整数) ……,两种运算交替重复进行.例 如:取 n=24,则:
A、 , B、 , C、 , D、 ,6. 定义一种对正整数 的“F”运算: ①当 为奇数时, ; ②当 为偶数时, (其中 是使 为奇数的正整数) ……,两种运算交替重复进行.例 如:取 n=24,则:
若 , 则第 2021 次“F”运算的结果是 ( )
A、1 B、4 C、22 D、7. 任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如: , , , …按此规律,若分裂后,其中有一个奇数是2023,则m的值是( )A、46 B、45 C、44 D、438. a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=-2,-2的“哈利数”是= , 已知 , 是的“哈利数”,是的“哈利数”,是的“哈利数”,…,依此类推,则=( )A、 B、 C、-3 D、9. 如图所示的是中国南宋数学家杨辉在详解《九章算法》中出现的三角形状的数列,又称为“杨辉三角形”该三角形中的数据排列有着一定的规律,若将其中组斜数列用字母、 , , 代替,如图 , 则的值为( ) A、9801 B、10000 C、10201 D、1050010. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“”方向排列,如 , , , , , , , 根据这个规律,第 334 个点的坐标为( )
A、9801 B、10000 C、10201 D、1050010. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“”方向排列,如 , , , , , , , 根据这个规律,第 334 个点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
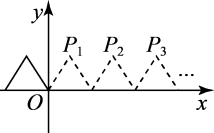
11. 对于正数x,规定 , 例如 , 则的结果是= .12. 如图,将边长为2的等边三角形沿x轴正方形连续翻折2001次,依次得到点 , , , , , 则点的坐标是 .
 13. 计算得: , , , , , …,则的个位数字是 .14. 做个一个数字游戏:
13. 计算得: , , , , , …,则的个位数字是 .14. 做个一个数字游戏:第一步:取一个自然数 , 计算
 得
得 ;
;第二步:算出
 的各位数字之和得
的各位数字之和得 , 计算
, 计算 得
得 ;
;第三步:算出
 的各位数字之和得
的各位数字之和得 , 计算
, 计算 得
得 ;
;以此类推,a3= , .
15. 观察等式:;;已知按一定规律排列的一组数:、、、、、 . 若 , 用含的式子表示这组数的和是 .16. 如图,是的外角,的平分线与的平分线交于点 , 的平分线与的平分线交于点 , …的平分线与的平分线交于点 , 设 , 则 .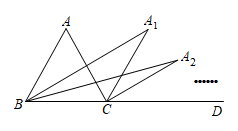
三、解答题