人教版备考2023中考数学二轮复习 专题34 探索规律问题----图形的规律
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 如图,中的与x轴重合,将绕原点O顺时针旋转后得到 , 将绕原点O顺时针旋转得到 , …,如此继续下去,连续旋转2023次得到 , 则点的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点。按照此规律,第n幅图中圆点的个数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3. 如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第2022次碰到矩形的边时的点为图中的( )
 A、点P B、点Q C、点M D、点N
A、点P B、点Q C、点M D、点N -
4. 如图,在矩形ABCD中,已知 , , 矩形在直线l上绕其右下角的顶点B向右旋转至图①位置,再绕右下角的顶点继续向右旋转至图②位置,…,以此类推,这样连续旋转2021次后,顶点A在整个旋转过程中所经过的路程之和是( )
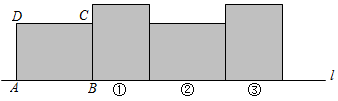 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 为庆祝国庆,小明用大小相等的五角星按一定规律摆出如下图案,则第15个图案五角星的颗数为( )
 A、46 B、49 C、52 D、55
A、46 B、49 C、52 D、55 -
6. 等边△ABC在数轴上的位置如图所示,点A、点B、点C对应的数分别为0,-0.5和–1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2022次后,点B所对应的数是( )
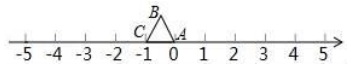 A、2021 B、2021.5 C、2022.5 D、2023
A、2021 B、2021.5 C、2022.5 D、2023 -
7. 如图,六边形是边长为1的正六边形,曲线叫做“正六边形的渐开线”,其中的圆心依次按点循环,一电子宠物从点出发,沿着“渐开线”爬至点的路径长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 如图所示,按大拇指食指中指无名指小指无名指中指食指大拇指食指的顺序,依次数正整数1,2,3,4,5,以此类推,当第2022次数到中指时,这个数是( )
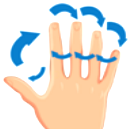 A、8085 B、8086 C、8087 D、8088
A、8085 B、8086 C、8087 D、8088 -
9. 如图, 在△ABC中, , 的平分线与的平分线交于点 , 得 , 的平分线与的平分线交于点 , 得 , …,的平分线与的平分线交于点 , 得 , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 如图,四边形ABCD中,AC=a,BD=b,且AC丄BD,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1 , 再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2…,如此进行下去,得到四边形AnBnCnDn . 下列结论正确的个数有
① 四边形A2B2C2D2是矩形;
② 四边形A4B4C4D4是菱形;
③ 四边形A5B5C5D5的周长是;
④ 四边形AnBnCnDn的面积是 .
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题
-
11. 下列是幼儿园小朋友用火柴棒拼出的一列图形。

第6个图中共有根火柴,第2008个图中有根火柴;
-
12. 如图,已知图①是一块边长为1,周长记为C1的等边三角形卡纸,把图①的卡纸剪去一个边长为的等边三角形纸板后得到图②,然后沿同一底边再剪去一个边长为的等边三角形后得到图③,依次剪去一个边长为、、…的等边三角形后,得到图④、⑤、⑥、…,记图n(n≥3)中的卡纸的周长为Cn , 则Cn-Cn-1= .

-
13. 如图,在x轴的正半轴上依次截取 , 过点分别作x轴的垂线与反比例函数的图象相交于点 , 得 , , , …,并设其面积分别为 , 则 . (n为正整数)

-
14. 李乐用相同的小三角形摆图形(如图),照这样摆下去,摆n个图形需要小三角形个.

-
15. 电子跳蚤游戏盘(如图)为三角形ABC,AB=6,AC=7,BC=8,如果电子跳蚤开始时在BC边的P0点,BP0=3,第一步跳蚤从P0跳到AC边上P1点,且CP1=CP0;第二步跳蚤从P1跳到AB边上P2点,且AP2=AP1;第三步跳蚤从P2跳回到BC边上P3点,且BP3=BP2;…跳蚤按上述规则跳下去,第n次落点为Pn,则P2022与C之间的距离为.

-
16. 图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小角形三边的中点,得到图3,按上面的方法继续下去.则图2中共有个三角形,第n个图形(图1是第一个图形)中共有个三角形(用含n的代数式表示).

-
17. 观察下列一组图形中点的个数,其中第1个图中共有 4 个点,第2个图中共有 10 个点,第3个图中共有 19 个点, 按此规律第4个图中共有点的个数比第3个图中共有点的个数多 个;第20个图中共有点的个数为 个.

三、解答题
-
18. 图1中,有一个平行四边形;
图2中,由2个相同的平行四边形拼成一排的图形,这图形中可以找到3个平行四边形;
图3中,由3个相同的平行四边形拼成一排的图形,这图形中可以找到6个平行四边形;

由此我们可以提出一个这样的问题:
图4中,由4个相同的平行四边形拼成一排的图形中,可以找到几个平行四边形?
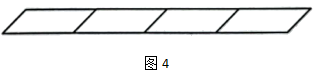
答:10个
请你根据以上事实,将一些相同的平行四边形横向或纵向拼接,由此提出一个数学问题,并写出答案.
-
19. 【观察发现】如图,我们通过观察后可以发现:两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;那么四条直线相交,最多有 ▲ 个交点;n条直线相交,最多有 ▲ 个交点(用含n的代数式表示);
【实践应用】在实际生活中同样存在数学规律型问题,请你类比上述规律探究,计算:某校七年级举办篮球比赛,第一轮要求每两班之间比赛一场,若七年级共有16个班,则这一轮共要进行多少场比赛?

-
20. 如图
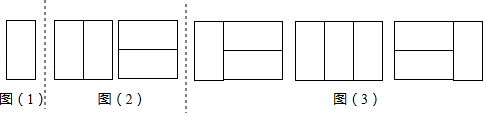
(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
(1)、探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
(2)、探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1 , an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 ▲ 种不同的镶嵌方案.
四、综合题
-
21. 如图, , 在内部作以点O为位似中心的正方形 , 正方形 , 正方形 , …,正方形 , 其对应顶点 , 都在射线上,对应顶点 , 都在射线上,将正方形的面积记作 , 正方形的面积记作 , 正方形的面积记作 , …,依此类推,正方形的面积记作 , .
 (1)、第5个正方形的面积(2)、第 n个正方形的面积(3)、若正方形的面积为 , 则这是第几个正方形?
(1)、第5个正方形的面积(2)、第 n个正方形的面积(3)、若正方形的面积为 , 则这是第几个正方形? -
22. 如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
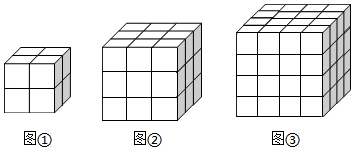 (1)、第1个几何体中只有2个面涂色的小立方体共有个;第2个几何体中只有2个面涂色的小立方体共有个;第3个几何体中只有2个面涂色的小立方体共有个.(2)、求出第10个几何体中只有2个面涂色的小立方体的块数.(3)、求出前100个几何体中只有2个面涂色的小立方体的块数的和.
(1)、第1个几何体中只有2个面涂色的小立方体共有个;第2个几何体中只有2个面涂色的小立方体共有个;第3个几何体中只有2个面涂色的小立方体共有个.(2)、求出第10个几何体中只有2个面涂色的小立方体的块数.(3)、求出前100个几何体中只有2个面涂色的小立方体的块数的和.
