人教版备考2023中考数学二轮复习专题32 新定义问题

试卷更新日期：2023-01-06 类型：二轮复习

进入出卷网下载

一、单选题

1. 定义新运算“※”的运算法则为：当 $a > 0$ ， $b > 0$ 时， $a ※ b = \sqrt{a + 2 b}$ ．例如： $6 ※ 4 = \sqrt{6 + 2 \times 4} = \sqrt{14}$ ．那么 $2 \times (4 ※ 6)$ 的值是（）

A、8 B、48 C、 $\sqrt{10}$ D、 $2 \sqrt{14}$

查看试题解析
2. 在实数范围内规定新运算“ $Δ$ ”，其规则是： $a Δ b = - 2 a + b$ ．已知不等式 $x Δ k \leq 1$ 的解集在数轴上如图表示，则 $k$ 的值是（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
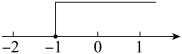3. 定义： $f (x$ ， $y) = (- x$ ， $- y)$ ， $g (a$ ， $b) = (b$ ， $a)$ ，例如： $f (1$ ， $2) = (- 1$ ， $- 2)$ ， $g (2$ ， $3) = (3$ ， $2)$ ，则g(f(5，-2))=（）

A、(2， -5) B、(-2，5) C、(-5，2) D、(-2，-5)

查看试题解析
4. 中国人很早就开始使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放着表示正数，斜放着表示负数，如图（1）表示 $(+ 2) + (- 2)$ ．按照这种表示法，如图（2）表示的是（）

A、 $(+ 3) + (+ 6)$ B、 $(- 3) + (- 6)$ C、 $(- 3) + (+ 6)$ D、 $(+ 3) + (- 6)$

查看试题解析
5. 已知 $y_{1}$ 和 $y_{2}$ 均是以x为自变量的函数，当 $x = n$ 时，函数值分别是 $N_{1}$ 和 $N_{2}$ ，若存在正数n，使得 $N_{1} + N_{2} = 1$ ，则称函数 $y_{1}$ 和 $y_{2}$ 是“正和谐函数”．下列函数 $y_{1}$ 和 $y_{2}$ 是“正和谐函数”的是（）

A、 $y_{1} = 2 x + 1$ 和 $y_{2} = 3 x + 2$ B、 $y_{1} = - x + 3$ 和 $y_{2} = 2 x - 1$ C、 $y_{1} = - x - 1$ 和 $y_{2} = 3 x - 2$ D、 $y_{1} = - x + 1$ 和 $y_{2} = 2 x + 3$

查看试题解析
6. 用“☆”定义一种新运算：对于任何不为零的整数 $a$ 和 $b$ ，规定 $a ☆ b = a^{2} - b^{2}$ ，如 $(- 1) ☆ 2 = {(- 1)}^{2} - 2^{2}$ ，则 $(- 3) ☆ (4 ☆ 5)$ 的值为（）

A、 $- 72$ B、 $- 9$ C、72 D、9

查看试题解析
7. 在新型冠状病毒防控战“疫”中，花溪榕筑花园小区利用如图①的建立了一个身份识别系统，图②是某个业主的识别图案，灰色小正方形表示1，白色小正方形表示0，将第一行数字从左到右依次记为a，b，c，d算式a×2³+b×2²+c×2¹+d×2⁰的运算结果为该业主所居住房子的栋数号．例如，图②第一行数字从左到右依次为0，1，0，1，通过计算得0×2³+1×2²+0×2¹+1×2⁰＝5，即可知该业主为5栋住户，小敏家住在11栋，则表示他家的识别图案是（）

A、 B、 C、 D、

查看试题解析
8. 对于实数a，b定义运算“ $\otimes$ ”为 $a \otimes b = b^{2} - a b$ ，例如 $3 \otimes 2 = 2^{2} - 3 \times 2 = - 2$ ，则关于x的方程 $(m + 2) \otimes x = 1 - m$ 的根的情况，下列说法正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
9. 在明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地锦”，如图1，计算 $82 \times 34$ ，将乘数82记入上行，乘数34记入右行，然后用乘数82的每位数字乘以乘数34的每位数字，将结果记入相应的格子中，最后按斜行加起来，既得2788．如图2，用“铺地锦”的方法表示两个两位数相乘，下列结论错误的是（）

A、b的值为6 B、a为奇数 C、a的值大于3 D、乘积结果可以表示为 $101 b + 10 （ a + 1 ） - 1$

查看试题解析
10. 数学上，为了简便把1到n的连续n个自然数的和记作 $\sum_{k = 1}^{n} k$ ，即 $\sum_{k = 1}^{n} k = 1 + 2 + 3 + \dots + n$ ；把1到n的连续n个自然数的乘积记作n！，即n！＝1×2×3×…×（n﹣1）×n；则 $\sum_{i = 1}^{2020} i - \sum_{i = 1}^{2021} i + \frac{2021!}{2020!}$ 的值为（）

A、0 B、1 C、2020 D、2021

查看试题解析
11. 形如 $a_{1} a_{2} \dots {a_{n}}_{－ 1} a_{n} {a_{n}}_{－ 1} a_{2} a_{1}$ 的自然数(其中 n为正整数， $a_{1} \leq a_{2} \leq \dots \leq {a_{n}}_{－ 1} \leq a_{n}$ ， $a_{1} > 0 ， a_{1} ， a_{2} ， \dots$ ， $a_{n}$ 为 $0 ， 1 ， \dots ， 9$ 中的数字)称为“单峰回文数”，不超过5位的“单峰回文数”的个数是（）

A、273 B、219 C、429 D、129

查看试题解析
12. 对于实数 $a ， b$ ，定义符号 $m i n {a ， b}$ 其意义为：当 $a \geq b$ 时， $m i n {a ， b} = b$ ；当 $a < b$ 时， $m i n {a ， b} = a$ ．例如： $m i n {2 ， - 1} = - 1$ ，若关于 $x$ 的函数 $y = m i n {2 x - 1 ， - x + 3}$ ，则该函数的最大值是（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{5}{3}$ D、2

查看试题解析
13. 张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子 $x + \frac{1}{x} (x > 0)$ 的最小值是 $2$ ”．其推导方法如下：在面积是 $1$ 的矩形中设矩形的一边长为 $x$ ，则另一边长是 $\frac{1}{x}$ ，矩形的周长是 $2 (x + \frac{1}{x})$ ；当矩形成为正方形时，就有 $x = \frac{1}{x} (x > 0)$ ，解得 $x = 1$ ，这时矩形的周长 $2 (x + \frac{1}{x}) = 4$ 最小，因此 $x + \frac{1}{x} (x > 0)$ 的最小值是 $2$ ．模仿张华的推导，你求得式子 $\frac{x^{2} + 4}{x} (x > 0)$ 的最小值是（）．

A、2 B、4 C、6 D、8

查看试题解析
14. 记实数 $x_{1}$ ， $x_{2}$ ， $\cdot \cdot \cdot$ ， $x_{n}$ 中的最大数为 $m a x {x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{n}}$ ，例如 $m a x {- 2 ， 0 ， 2} = 2$ ，则函数 $y = m a x {- 3 x - 3 ， 2 - x ， x}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

15. 定义：对于一个数 $x$ ，我们把 $[x]$ 称作 $x$ 的相伴数；若 $x \geq 0$ ，则 $[x] = x - 1$ ；若 $x < 0$ ，则 $[x] = x + 1$ ．例 $[\frac{3}{2}] =$ $\frac{1}{2}$ ， $[- 2]$ $=$ $- 1$ ；已知当 $a > 0$ ， $b < 0$ 时有 $[a] = [b] + 1$ ，则代数式 $(b - a)^{3} - 3 a + 3 b$ 的值为．

查看试题解析
16. 对于任何有理数，我们规定符号 $\begin{array}{l} a & b \\ c & d \end{array}$ 的意义是 $\begin{array}{l} a & b \\ c & d \end{array} = a d - b c$ ，如 $\begin{array}{l} 1 & 2 \\ 3 & 4 \end{array} = 1 \times 4 - 2 \times 3 = - 2 .$ 当 $| x - 3 | + (y + 1)^{2} = 0$ 时， $\begin{array}{l} x^{2} - y & 2 \\ x^{2} & - 1 \end{array}$ 值为.

查看试题解析
17. 现定义一个新运算“※”，规定对于任意实数x，y，都有 $x ※ y = \sqrt{x + y} + \sqrt[3]{x y + 1}$ ，则 $7 ※ 9$ 的值为．

查看试题解析
18. 利用平方与开平方互为逆运算的关系，可以将某些无理数进行如下操作：例如： $a = \sqrt{3} + 1$ 时，移项得 $a - 1 = \sqrt{3}$ ，两边平方得 $(a - 1)^{2} = (\sqrt{3})^{2}$ ，所以 $a^{2} - 2 a + 1 = 3$ ，即得到整系数方程： $a^{2} - 2 a - 2 = 0$ ．仿照上述操作方法，完成下面的问题：当 $a = \frac{\sqrt{5} - 1}{2}$ 时，①得到的整系数方程为；②计算： $a^{3} - 2 a + 2025 =$ ．

查看试题解析
19. 新定义一种运算： $a ◎ b = a^{2} - 2 b$ ，例如： $(- 1) ◎ 3 = {(- 1)}^{2} - 2 \times 3 = 1 - 6 = - 5$ ，则 $[- 2 ◎ (- 1)] ◎ 4 =$ ．

查看试题解析
20. 如图，约定：上方相邻两数之和等于这两数下方箭头共同指向的数.
示例：，即 $4 + 3 = 7$ .
问题：如图
当 $y = - 2$ 时，n的值为.

查看试题解析
21. 对于实数a，b，定义运算“*”： $a*b = a^{2} － ab (a \leq b)$ ； $a*b = b^{2} － ab (a > b)$ ，关于x的方程 $(2 x － 1) * (x － 1) = m$ 恰好有三个不相等的实数根，则m的取值范围是．

查看试题解析
22. 我们知道，互相垂直且有公共原点的两条数轴构成平面直角坐标系．如果坐标系中两条坐标轴不垂直，那么这样的坐标系称为“斜坐标系”．如图1，P是斜坐标系 $x O y$ 中的任意一点，与直角坐标系相类似，过点P分别作两坐标轴的平行线，与x轴、y轴交于点M、N，若M、N在x轴、y轴上分别对应实数a、b，则有序实数对 $(a ， b)$ 叫做点P在斜坐标系 $x O y$ 中的坐标．如图2，在斜坐标系 $x O y$ 中，已知点 $B (4 ， 0)$ 、点 $C (0 ， 3) ， P (x ， y)$ 是线段 $B C$ 上的任意一点，试求x、y之间一定满足的一个等量关系式：．

查看试题解析

三、解答题

23. 阅读材料，求 $1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots + 2^{2017}$ 的值．
解：设 $S = 1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots + 2^{2017}$ ，将等式两边同时乘2，得 $2 S = 2 + 2^{2} + 2^{3} + 2^{4} + \dots + 2^{2018}$ ，所以 $2 S - S = 2^{2018} - 1$ ，即 $S = 2^{2018} - 1$ ，即 $1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots + 2^{2017} = 2^{2018} - 1$ 请你仿照此方法解决下列问题：

求： $1 + 3 + 3^{2} + 3^{3} + 3^{4} + \dots + 3^{2022}$ ．

查看试题解析
24. 定义：若一个一元二次方程的“某一个根”是另一个一元二次方程的一个根，则称这两个方程为“友好方程”．已知关于 $x$ 的一元二次方程 $x^{2} = 3 x$ 与 $x^{2} - 2 x + m - 1 = 0$ 是“友好方程”，求 $m$ 的值．

查看试题解析
25. 实际问题：
各边长都是整数，最大边长为31的三角形有多少个？
问题建模：为解决上面的数学问题，我们先研究下面的数学模型。
在1～n这n个自然数中，每次取两个数（可重复），使得所取的两个数之和大于n，有多少种不同的取法？
为了找到解决问题的方法，我们把上面数学模型简单化．
探究一：
在1～4这4个自然数中，每次取两个数（可重复），使得所取的两个数之和大于4，有多少种不同的取法？
第一步：在1～4这4个自然数中，每次取两个不同的数，使得所取的两个数之和大于4，根据题意，有下列取法：1+4，2+3，2+4，3+2，3+4，4+1，4+2，4+3；而1+4与4+1，2+3与3+2，…是同一种取法，所有上述每一种取法都重复过一次，因此共有 $\frac{1 + 2 + 2 + 3}{4} = 4 = \frac{4^{2}}{4}$ 种不同的取法．
第二步：在1～4这4个自然数中，每次取两个相同的数，使得所取的两个数之和大于4，有下列取法：3+3，4+4，因此有2种不同的取法．
综上所述，在1～4这4个自然数中，每次取两个数（可重复），使得所取的两个数之和大于4，有 $\frac{4^{2}}{4} + 2$ 种不同的取法．
探究二：
在1～5这5个自然数中，每次取两个数（可重复），使得所取的两个数之和大于5，有多少种不同的取法？
第一步：在1～5这5个自然数中，每次取两个不同的数，使得所取的两个数之和大于5，根据题意，有下列取法：1+5，2+4，2+5，3+4，3+5，4+2，4+3，4+5，5+1，5+2，5+3，5+4；而1+5与5+1，2+4与4+2，…是同一种取法，所有上述每一种取法都重复过一次，因此共有 $\frac{1 + 2 + 2 + 3 + 4}{4} = 6 = \frac{5^{2} - 1}{4}$ 种不同的取法．
第二步：在1～5这5个自然数中，每次取两个相同的数，使得所取的两个数之和大于5，有下列取法：3+3，4+4，5+5因此有3种不同的取法．
综上所述，在1～5这5个自然数中，每次取两个数（可重复），使得所取的两个数之和大于5，有 $\frac{5^{2} - 1}{4} + 3$ 种不同的取法．
探究三：
在1～6这6个自然数中，每次取两个数（可重复），使得所取的两个数之和大于6，有多少种不同的取法？（仿照探究二写出探究过程）
探究四：
在1～7这7个自然数中，每次取两个数（可重复），使得所取的两个数之和大于7，有      ▲ 种不同的取法．
探究五：
在1～n（n为偶数）这n个自然数中，每次取两个数（可重复），使得所取的两个数之和大于n，有      ▲ 种不同的取法．
探究六：
在1～n（n为奇数）这n个自然数中，每次取两个数（可重复），使得所取的两个数之和大于n，有      ▲ 种不同的取法．
问题解决：
①各边长都是整数，最大边长为20的三角形有      ▲ 个；
②各边长都是整数，最大边长为31的三角形有      ▲ 个．

查看试题解析

四、综合题

26. 阅读下列材料：让我们来规定一种运算： $| \begin{array}{l} a \\ c \end{array}$    $\begin{array}{l} b \\ d \end{array} | = a d - b c$ ，例如： $| \begin{array}{l} 2 \\ 3 \end{array}$    $\begin{array}{l} 4 \\ 1 \end{array} | = 2 \times 1 - 4 \times 3 = - 10$ ，再如： $| \begin{array}{l} x \\ y \end{array}$    $\begin{array}{l} 6 \\ 2 \end{array} | = 2 x - 6 y$ ．按照这种运算的规定：请解答下列各个问题：

(1)、 $| \begin{array}{l} - 2 \\ 4 \end{array}$    $\begin{array}{l} - 5 \\ 3 \end{array} | =$ ．

(2)、当 $| \begin{array}{l} x \\ 1 \end{array}$     $\begin{array}{l} 1 - x \\ 2 \end{array} | = 0$ 时，求x的值．

(3)、将下面式子进行因式分解： $| \begin{array}{l} x^{2} - 2 x \\ - 3 \end{array}$    $\begin{array}{l} 8 \\ x^{2} - 2 x - 11 \end{array} |$

查看试题解析
27. 我们规定：两组邻边分别相等的四边形叫做筝形四边形，如图1，四边形 $A B C D$ 中，若 $A B = A D$ ， $C B = C D$ ，则称四边形 $A B C D$ 是筝形四边形．

(1)、如图2，筝形 $A B C D$ 中， $A B = A D$ ， $C B = C D$ ，对角线 $A C$ ， $B D$ 相交于点 $E$ ．
①求证： $A C$ 垂直平分 $B D$ ；
②若 $∠ B A D + ∠ B C D = 180 °$ ，求证： $∠ A D B = ∠ D C A$ ；

(2)、如图3，筝形四边形 $A B C D$ 中， $A B = A D$ ， $C B = C D$ ，对角线 $A C$ ， $B D$ 相交于点 $E$ ，若 $A B = C B$ ，求证： $A C$ ， $B D$ 互相垂直平分．

查看试题解析

人教版备考2023中考数学二轮复习 专题32 新定义问题

一、单选题

二、填空题

三、解答题

四、综合题

人教版备考2023中考数学二轮复习专题32 新定义问题