人教版备考2023中考数学二轮复习 专题31 动态几何
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 如图,已知在中, , 点D沿自B向C运动,作于E,于F,则的值y与的长x之间的函数图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
2. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )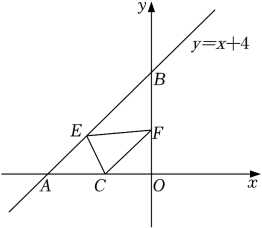 A、 , B、 , C、 , D、 ,3. 已知,直线l:与x轴交于点A,点B与点A关于y轴对称.M是直线l上的动点,将OM绕点O逆时针旋转60°得ON.连接BN,则线段BN的最小值为( )
A、 , B、 , C、 , D、 ,3. 已知,直线l:与x轴交于点A,点B与点A关于y轴对称.M是直线l上的动点,将OM绕点O逆时针旋转60°得ON.连接BN,则线段BN的最小值为( )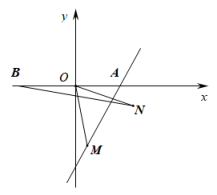 A、 B、3 C、 D、4. 如图,已知抛物线经过点 , , 与y轴交于点 , P为AC上的一个动点,则有以下结论:①抛物线的对称轴为直线;②抛物线的最大值为;③;④OP的最小值为 . 则正确的结论为( )
A、 B、3 C、 D、4. 如图,已知抛物线经过点 , , 与y轴交于点 , P为AC上的一个动点,则有以下结论:①抛物线的对称轴为直线;②抛物线的最大值为;③;④OP的最小值为 . 则正确的结论为( ) A、①②④ B、①② C、①②③ D、①③④5. 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
A、①②④ B、①② C、①②③ D、①③④5. 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( ) A、 B、 C、 D、36. 如图,在平面直角坐标系中,线段AB的端点 , 若直线与线段AB有交点,则k的值可能是( )
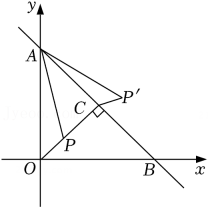
A、 B、 C、 D、36. 如图,在平面直角坐标系中,线段AB的端点 , 若直线与线段AB有交点,则k的值可能是( ) A、2 B、3 C、 D、-47. 如图,在平面直角坐标系 xOy 中,直线 y=-x+4 与坐标轴交于 A,B 两点,OC⊥AB 于点 C,P 是线段 OC 上的一个动点,连接 AP,将线段 AP 绕点 A 逆时针旋转 45°,得到线段 AP',连接 CP',则线段 CP'的最小值为( )
A、2 B、3 C、 D、-47. 如图,在平面直角坐标系 xOy 中,直线 y=-x+4 与坐标轴交于 A,B 两点,OC⊥AB 于点 C,P 是线段 OC 上的一个动点,连接 AP,将线段 AP 绕点 A 逆时针旋转 45°,得到线段 AP',连接 CP',则线段 CP'的最小值为( )
 A、 B、 C、2 D、8. 如图,在平面直角坐标系中,平行四边形OABC的顶点O在坐标原点,点E是对角线AC上一动点(不包含端点),过点E作EFBC,交AB于F,点P在线段EF上.若OA=4,OC=2,∠AOC=45°,EP=3PF,P点的横坐标为m,则m的取值范围是( )
A、 B、 C、2 D、8. 如图,在平面直角坐标系中,平行四边形OABC的顶点O在坐标原点,点E是对角线AC上一动点(不包含端点),过点E作EFBC,交AB于F,点P在线段EF上.若OA=4,OC=2,∠AOC=45°,EP=3PF,P点的横坐标为m,则m的取值范围是( )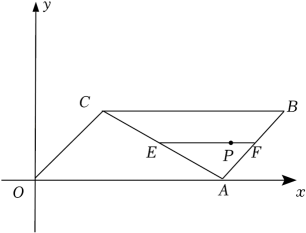 A、 B、 C、 D、9. 已知 ,抛物线 顶点在线段 上运动,形状保持不变,与 轴交于 两点( 在 的右侧),下列结论:
A、 B、 C、 D、9. 已知 ,抛物线 顶点在线段 上运动,形状保持不变,与 轴交于 两点( 在 的右侧),下列结论:①. ;②.当 时,一定有 随 的增大而增大;③.若点 横坐标的最小值为-5,点 横坐标的最大值为3;④.当四边形 为平行四边形时, .
其中正确的是( )
A、①③ B、②③ C、①④ D、①③④10. 如图①,已知 的斜边 和正方形 的边 都在直线 上( ),且点 与点 重合, 沿直线 向右匀速平移,当点 与点 重合时, 停止运动,设 被 截得的线段长 与 平移的距离 之间的函数图象如图②,则当 时, 和正方形 重合部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
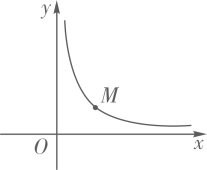
11. 如图,点M是反比例函数y(x>0)图像上一点,将点M绕原点O逆时针旋转45°后,恰好落在y轴的正半轴上,则线段OM的长为 .
 12. 如图,把放在平面直角坐标系内,其中 , , 点 , 的坐标分别为 , . 当直线(为常数)与有交点时,则的取值范围是 .
12. 如图,把放在平面直角坐标系内,其中 , , 点 , 的坐标分别为 , . 当直线(为常数)与有交点时,则的取值范围是 . 13. 已知:直线y=-x+1与x轴、y轴分别交于点A、点B,当点P在直线上运动时,平面内存在点Q,使得以点O、P、B、Q为顶点的四边形是菱形,请你写出所有满足条件的点Q的坐标 .14. 如图,在平面直角坐标系中,已知第一象限上的点A(m,n)是双曲线上的动点,过点A作AM∥y轴交x轴于点M,过点N(0,2n)作NB∥x轴交双曲线于点B,交直线AM于点C,若四边形OACB的面积为4,则k的值为 .
13. 已知:直线y=-x+1与x轴、y轴分别交于点A、点B,当点P在直线上运动时,平面内存在点Q,使得以点O、P、B、Q为顶点的四边形是菱形,请你写出所有满足条件的点Q的坐标 .14. 如图,在平面直角坐标系中,已知第一象限上的点A(m,n)是双曲线上的动点,过点A作AM∥y轴交x轴于点M,过点N(0,2n)作NB∥x轴交双曲线于点B,交直线AM于点C,若四边形OACB的面积为4,则k的值为 . 15. 一个玻璃杯竖直放置时的纵向截面如图1所示,其左右轮廓线 , 为同一抛物线的一部分, , 都与水平地面平行,当杯子装满水后 , , 液体高度 , 将杯子绕倾斜倒出部分液体,当倾斜角时停止转动,如图2所示,此时液面宽度 , 液面到点所在水平地面的距离是 .
15. 一个玻璃杯竖直放置时的纵向截面如图1所示,其左右轮廓线 , 为同一抛物线的一部分, , 都与水平地面平行,当杯子装满水后 , , 液体高度 , 将杯子绕倾斜倒出部分液体,当倾斜角时停止转动,如图2所示,此时液面宽度 , 液面到点所在水平地面的距离是 . 16. 如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A,B两点,过点A的直线交y轴正半轴于点M,且 . 在平面直角坐标系内存在点C,使得以A,B,M,C为顶点的四边形是平行四边形,则点C的坐标为 .
16. 如图,在平面直角坐标系中,函数的图象分别交x轴,y轴于A,B两点,过点A的直线交y轴正半轴于点M,且 . 在平面直角坐标系内存在点C,使得以A,B,M,C为顶点的四边形是平行四边形,则点C的坐标为 . 17. 如图,平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,点C的坐标是 . 在y轴上有一个动点M,当△MDC的周长最小的时候,点M的坐标是 .
17. 如图,平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,点C的坐标是 . 在y轴上有一个动点M,当△MDC的周长最小的时候,点M的坐标是 . 18. 如图,抛物线y=x2+x+3与x轴交于点A、点B,与y轴交于点C,点F为抛物线的顶点,在抛物线的对称轴上存点G,当点G的坐标为时△AFG为等腰三角形.
18. 如图,抛物线y=x2+x+3与x轴交于点A、点B,与y轴交于点C,点F为抛物线的顶点,在抛物线的对称轴上存点G,当点G的坐标为时△AFG为等腰三角形.
三、综合题
-
19. 如图在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与直线交于点P.
 (1)、A点坐标为 , P点坐标为;(2)、在线段上有一个动点M,过M点作直线轴,与直线相交于点N,若的面积为 , 求M点的坐标.(3)、若点C为线段上一动点,在平面内是否存在一点D,使得以点O,A,C,D为顶点的四边形是菱形,若存在请直接写出D点的坐标,若不存在请说明理由.20. 如图,二次函数的图象交y轴于点C,点B与点C关于该二次函数图象的对称轴对称,已知一次函数的图象经过该二次函数图象上的点及点B.
(1)、A点坐标为 , P点坐标为;(2)、在线段上有一个动点M,过M点作直线轴,与直线相交于点N,若的面积为 , 求M点的坐标.(3)、若点C为线段上一动点,在平面内是否存在一点D,使得以点O,A,C,D为顶点的四边形是菱形,若存在请直接写出D点的坐标,若不存在请说明理由.20. 如图,二次函数的图象交y轴于点C,点B与点C关于该二次函数图象的对称轴对称,已知一次函数的图象经过该二次函数图象上的点及点B. (1)、求二次函数与一次函数的解析式.(2)、点P是该抛物线上一动点,点P从A点沿抛物线向B点运动(点P不与A、B重合),过点P作轴,PD交直线AB于点D.请求出点P在运动的过程中,线段PD的长度的最大值以及此时点P的坐标;(3)、抛物线上是否存在点Q,使 , 若存在,请直接写出点Q的坐标;若不存在,请说明理由.21. 已知抛物线具有如下性质:给抛物线上任意一点到定点的距离与到x轴的距离相等,如图,点M的坐标为 , P是抛物线上一动点,则
(1)、求二次函数与一次函数的解析式.(2)、点P是该抛物线上一动点,点P从A点沿抛物线向B点运动(点P不与A、B重合),过点P作轴,PD交直线AB于点D.请求出点P在运动的过程中,线段PD的长度的最大值以及此时点P的坐标;(3)、抛物线上是否存在点Q,使 , 若存在,请直接写出点Q的坐标;若不存在,请说明理由.21. 已知抛物线具有如下性质:给抛物线上任意一点到定点的距离与到x轴的距离相等,如图,点M的坐标为 , P是抛物线上一动点,则 (1)、当面积为4时,求P点的坐标;(2)、求周长的最小值.22. 综合与探究:
(1)、当面积为4时,求P点的坐标;(2)、求周长的最小值.22. 综合与探究:如图1,平面直角坐标系中,一次函数的图象分别交x轴、y轴于点A,B,一次函数的图象经过点A,并与y轴交于点C.
 (1)、求A,B两点的坐标及k的值;(2)、如图2,若点P是x轴正半轴上的一个动点,过点P作x轴的垂线,分别交直线 于点M,N.设点P的横坐标为 .
(1)、求A,B两点的坐标及k的值;(2)、如图2,若点P是x轴正半轴上的一个动点,过点P作x轴的垂线,分别交直线 于点M,N.设点P的横坐标为 .①当点P在线段上时,用含m的代数式表示线段MN的长为;
②请从A,B两题中任选一题作答.我选择题.
A.在点P运动的过程中,当时,求点P的坐标.
B.作点M关于x轴的对称点 , 在点P运动过程中,当时,求点P的坐标.
23. 如图,直线与x轴交于点B,与y轴交于点C,对称轴为的抛物线经过B,C两点,与x轴负半轴交于点A.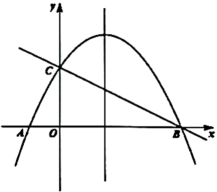 (1)、求抛物线的解析式;(2)、P为抛物线上的一点,连接 , 将线段绕点A顺时针旋转得线段 , 当点Q到对称轴距离为时,求点P的坐标;(3)、M为抛物线上的动点,N在直线上,当以O,C,M,N为顶点的四边形为平行四边形时,直接写出点N的坐标.24. 综合与实践
(1)、求抛物线的解析式;(2)、P为抛物线上的一点,连接 , 将线段绕点A顺时针旋转得线段 , 当点Q到对称轴距离为时,求点P的坐标;(3)、M为抛物线上的动点,N在直线上,当以O,C,M,N为顶点的四边形为平行四边形时,直接写出点N的坐标.24. 综合与实践如图,抛物线与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C,点D是抛物线上的一动点.
 (1)、求A,B,C三点的坐标;(2)、如图2,当点D在第四象限时,连接和 , 得到 , 当的面积最大时,求点D的坐标;(3)、点E在x轴上运动,以点B,C,D,E为顶点的四边形是平行四边形,请借助图1探究,直接写出点E的坐标.25. 综合与实践
(1)、求A,B,C三点的坐标;(2)、如图2,当点D在第四象限时,连接和 , 得到 , 当的面积最大时,求点D的坐标;(3)、点E在x轴上运动,以点B,C,D,E为顶点的四边形是平行四边形,请借助图1探究,直接写出点E的坐标.25. 综合与实践如图,抛物线与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C,点D是抛物线上的一动点.
 (1)、求A,B,C三点的坐标;(2)、如图2,当点D在第四象限时,连接和 , 得到 , 当的面积最大时,求点D的坐标;(3)、点E在x轴上运动,以点B,C,D,E为顶点的四边形是平行四边形,请借助图1探究,直接写出点E的坐标.26. 如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(1)、求A,B,C三点的坐标;(2)、如图2,当点D在第四象限时,连接和 , 得到 , 当的面积最大时,求点D的坐标;(3)、点E在x轴上运动,以点B,C,D,E为顶点的四边形是平行四边形,请借助图1探究,直接写出点E的坐标.26. 如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点. (1)、求该抛物线的解析式;(2)、在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大,若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.27. 如图,已知抛物线的图像与轴交于 , 两点,与轴交于点 .
(1)、求该抛物线的解析式;(2)、在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大,若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.27. 如图,已知抛物线的图像与轴交于 , 两点,与轴交于点 . (1)、求抛物线的解析式;(2)、点是直线下方抛物线上一点,当的面积最大时,求出点的坐标;28. 综合与探究
(1)、求抛物线的解析式;(2)、点是直线下方抛物线上一点,当的面积最大时,求出点的坐标;28. 综合与探究如图,已知抛物线与轴交于 , 两点(点在点的左侧),与轴交于点 .
 (1)、求抛物线的解析式;(2)、在抛物线的对称轴上存在一点 , 使得的值最小,此时点的坐标为;(3)、点是第一象限内抛物线上的一个动点(不与点 , 重合),过点作轴于点 , 交直线于点 , 连接 , 直线把的面积分成两部分,使 , 请求出点的坐标;(4)、若为抛物线的对称轴上的一个动点,是否存在点 , 使得是以为直角边的直角三角形,若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线的对称轴上存在一点 , 使得的值最小,此时点的坐标为;(3)、点是第一象限内抛物线上的一个动点(不与点 , 重合),过点作轴于点 , 交直线于点 , 连接 , 直线把的面积分成两部分,使 , 请求出点的坐标;(4)、若为抛物线的对称轴上的一个动点,是否存在点 , 使得是以为直角边的直角三角形,若存在,请直接写出点的坐标;若不存在,请说明理由.