人教版备考2023中考数学二轮复习专题29 数据分析

试卷更新日期：2023-01-05 类型：二轮复习

进入出卷网下载

一、单选题

1. 若一组数据 $x ， 1 ， 4$ 的中位数为3，则 $x$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 为深入落实“立德树人”的根本任务，坚持德、智、体、美、劳全面发展，某学校积极推进学生综合素质评价改革，某同学在本学期德智体美劳的评价得分如图所示，则该同学五项评价得分的众数，中位数，平均数分别为（）

A、8，8，8 B、7，7，7.8 C、8，8，8.6 D、8，8，8.4

查看试题解析
3. 欣欣商店在一段时间内销售了四种饮料共100瓶，各品牌饮料的销售量如表，根据表中数据，建议该商店进货数量最多的品牌是（）

品牌

甲

乙

丙

丁

销售量（瓶）

15

30

12

43

A、甲品牌 B、乙品牌 C、丙品牌 D、丁品牌

查看试题解析
4. 小红在“养成阅读习惯，快乐阅读，健康成长”读书大赛活动中，随机调查了本校初二年级20名同学，在近5个月内每人阅读课外书的数量，数据如下表所示：
人数
3
4
8
5
课外书数量（本）
12
13
15
18
则阅读课外书数量的中位数和众数分别是（）

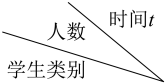
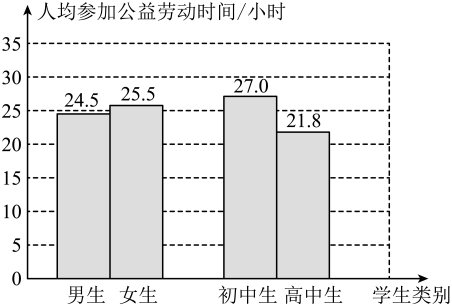
A、13，15 B、14，15 C、13，18 D、15，15

查看试题解析
5. 某校举行体操比赛，甲、乙两个班各选18名学生参加比赛，两个班参赛学生的平均身高都是1.72米，其方差分别是 $S_{甲}^{2} = 3.24$ ， $S_{乙}^{2} = 1.63$ ，则参赛学生身高比较整齐的班级是（）

A、甲班 B、乙班 C、同样整齐 D、无法确定

查看试题解析
6. 某校共有200名学生．为了解本学期学生参加公益劳动的情况，收集了他们参加公益劳动时间（单位：小时）等数据．下图是根据数据绘制的统计图表的一部分．下面有四个推断：
①这200名学生参加公益劳动时间的平均数一定在 $24.5 \sim 25.5$ 之间；②这200名学生参加公益劳动时间的中位数在 $20 ∼ 30$ 之间；③这200名学生中的初中生参加公益劳动时间的中位数一定在 $20 ∼ 30$ 之间；④这200名学生中的高中生参加公益劳动时间的中位数可能在 $20 ∼ 30$ 之间．
所有合理推断的序号是（）
$0 \leq t < 10$
$10 \leq t < 20$
$20 \leq t < 30$
$30 \leq t < 40$
$t \geq 40$
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中

A、①③ B、②④ C、①②③ D、①②③④

查看试题解析
7. 为了从甲、乙两名同学中选出一名同学代表班级参加学校的投篮比赛，对甲、乙两人进行了5次投篮试投比赛，试投每人每次投球10个，两人5次试投的成绩统计图如图所示．以下说法错误的是（）

A、甲同学5次试投进球个数的众数是8 B、甲、乙两名同学投篮成绩甲较稳定 C、甲、乙同学5次试投进球个数的平均数相同 D、乙同学5次试投进球个数的中位数是8

查看试题解析
8. 某同学对一组数据23，31，32，43，32，5◆，52进行统计分析时，发现其中一个两位数的个位数字被污染看不到了，则下列计算结果一定与被污数字无关的是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
9. 若一组数据 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 的平均数为4，方差为3，那么数据 $a_{1} + 2$ ， $a_{2} + 2$ ， $a_{3} + 2$ 的平均数和方差分别是（）

A、4， 3 B、6 $，$ 3 C、3 $，$ 4 D、6 5

查看试题解析
10. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ =（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析

二、填空题

11. 测量一袋水泥的质量，七次测得的数据分别是： $50 .4kg，50 .6kg，50 .8kg，49 .1kg，49kg$ ， $49 .6kg，50 .5kg$ ．这七次测量的平均值是．

查看试题解析
12. 农科院计划为某地选择合适的水果玉米种子，通过实验，甲、乙、丙、丁四种水果玉米种子每亩平均产量都是1500kg，方差分别为 $S_{甲}^{2} = 0.02$ ， $S_{乙}^{2} = 0.02$ ， $S_{丙}^{2} = 0.03$ ， $S_{丁}^{2} = 0.01$ ，则这四种水果玉米种子产量最稳定的是．（填“甲”“乙”“丙”“丁”）

查看试题解析
13. 某校体育期末考核“仰卧起坐”和“800米”两项，并按 $4 ： 6$ 的比重算出期末成绩．已知小林这两项的考试成绩分别为80分、90分，则小林的体育期末成绩为分．

查看试题解析
14. 袁隆平院士被誉为“世界杂交水稻之父”，他研究的水稻，不仅高产，而且抗倒伏.在某次实验中，他的团队对甲、乙两种水稻品种进行产量稳定实验，各选取了8块条件相同的试验田，同时播种并核定亩产，结果甲、乙两种水稻的平均亩产量相同，为了保证产量稳定，该团队决定推广乙品种，由此可知，甲品种的亩产量方差 $s_{甲}^{2}$ 乙品种的亩产量方差 $s_{乙}^{2}$ .(填“>”“<"或“ $=$ ")。

查看试题解析
15. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

查看试题解析

三、作图题

16. 为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶

10

次，为了比较两人的成绩，制作了如下统计图表：

甲乙射击成绩统计表

	平均数	中位数	方差	命中 $10$ 环的次数
甲	$7$			$0$
乙		$7.5$	$5.4$	$1$

甲乙射击成绩折线图

(1)、请补全上述图表（请直接在统计表中填空和补全折线图）；

(2)、如果规定成绩较稳定者胜出，则胜出，理由是；

(3)、如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？说明理由．

查看试题解析

17. 某班实行小组量化考核制．为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：

综合评价得分统计表（单位：分）

周次

组别

一

二

三

四

五

六

甲组

乙组

(1)、请根据表中的数据完成下表（注：方差的计算结果精确到0.1）

	平均数	中位数	方差
甲组		14
乙组	14		11.7

(2)、根据综合评价得分统计表中的数据，请在如图中画出乙组综合评价得分的折线统计图．

(3)、根据折线统计图中的信息，请你分别对甲、乙两个小组连续六周的学习情况作出简要评价．

查看试题解析

四、解答题

18. 学校运动会开设了“抢收抢种”项目，八(5)班甲，两个队伍都想代表班级参赛，为了选择一个比较好的队伍，八(5)班的班委组织了一次选拔赛，甲，乙两队各5人的比赛成绩如下表(单位：分)：

甲队

7

8

10

7

9

乙对

7

8

7

9

9

经计算，甲队比赛成绩的平均数为8分，方差为1.2，请计算乙队比赛成绩的方差，并根据计算结果，帮助班委选择一个成绩比较稳定的队伍代表班级参赛.

查看试题解析
19. 在校园诗歌朗诵比赛中，采用10位评委现场打分，每位选手的最后得分为去掉一个最低分，去掉一个最高分后的平均分，已知10位评委给某位选手的打分分别是：9.0 9.4 9.3 9.8 9.5 9.1 9.6 9.4 9.7 9.6
求这位选手的最后得分．

查看试题解析

五、综合题

20. 山西某中学王老师为了选拔一名优秀的学生参加市内的数学比赛，对两名备赛选手进行了6次测验，两位同学的测验成绩如表所示：
（参考公式 $S^{2} = \frac{(x_{1} - \bar{x})^{2} + (x_{2} - x)^{2} + ⋯ + (x_{n} - \bar{x})^{2}}{n}$ ）

第1次
第2次
第3次
第4次
第5次
第6次
平均成绩
中位数
众数
方差
甲
83
85
90
80
85
87
85
a
85
b
乙
86
86
83
84
85
86
c
85.5
d
$\frac{4}{3}$
根据表中提供的数据，解答下列问题：

(1)、a的值为， d的值为．

(2)、求b和c的值，并直接指出哪位同学的成绩更稳定．

(3)、根据以上信息，你认为王老师应该选哪位同学参加比赛，请说明理由．

查看试题解析

21. 某学校为落实立德树人根本任务，使每个学生都能得到全面而个性的发展，特举办了“科学竞赛”活动，甲、乙两个班学生的成绩统计如下：

分数/分	50	60	70	80	90	100
甲班人数/人	2	5	10	18	14	1
乙班人数/人	4	4	16	4	18	4

活动规定：以60分为及格线，并分别设置了一、二、三等奖，100分为一等奖，90分为二等奖，80分为三等奖．小亮分别计算了两个班的平均分和方差，得： ${\bar{x}}_{甲} = 78$ ， ${\bar{x}}_{乙} = 78$ ， ${\bar{x}}_{甲}^{2} = 128$ ， ${\bar{x}}_{乙}^{2} = 200$ ．请你根据以上材料回答下列问题．

(1)、甲、乙两个班的中位数和众数分别是多少？

(2)、你认为甲、乙两个班哪个班的成绩更优秀？为什么？

(3)、该校从得100分的两男三女5人中，随机选取2人参加教育局组织的竞赛，请你用列表或画树状图的方法，求出恰好选取一男一女参赛的概率．

查看试题解析

		$0 \leq t < 10$	$10 \leq t < 20$	$20 \leq t < 30$	$30 \leq t < 40$	$t \geq 40$
性别	男	7	31	25	30	4
性别	女	8	29	26	32	8
学段	初中		25	36	44	11
学段	高中

	第1次	第2次	第3次	第4次	第5次	第6次	平均成绩	中位数	众数	方差
甲	83	85	90	80	85	87	85	a	85	b
乙	86	86	83	84	85	86	c	85.5	d	$\frac{4}{3}$

品牌	甲	乙	丙	丁
销售量（瓶）	15	30	12	43

人数	3	4	8	5
课外书数量（本）	12	13	15	18

甲队	7	8	10	7	9
乙对	7	8	7	9	9

人教版备考2023中考数学二轮复习 专题29 数据分析

一、单选题

二、填空题

三、作图题

四、解答题

五、综合题

人教版备考2023中考数学二轮复习专题29 数据分析