人教版备考2023中考数学二轮复习 专题27 投影与视图
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 如图是某几何体的从三个不同方向看到的图形,则这个几何体是( )
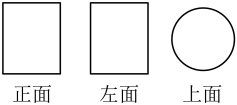 A、圆柱 B、正方体 C、球 D、圆锥2. 如图是由5个相同的正方体搭成的几何体,这个几何体的俯视图是( )
A、圆柱 B、正方体 C、球 D、圆锥2. 如图是由5个相同的正方体搭成的几何体,这个几何体的俯视图是( )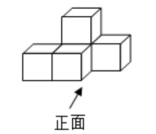 A、
A、 B、
B、 C、
C、 D、
D、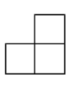 3. 该图形从哪个方向看是轴对称图形( )
3. 该图形从哪个方向看是轴对称图形( ) A、从正面看 B、从上面看 C、从左面看 D、都不是4. 如图所示的几何体的左视图( )
A、从正面看 B、从上面看 C、从左面看 D、都不是4. 如图所示的几何体的左视图( ) A、
A、 B、
B、 C、
C、 D、
D、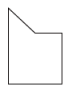 5. 如图是一根空心方管,在研究物体的三种视图时,小明画出的该空心方管的主视图与俯视图分别是( )
5. 如图是一根空心方管,在研究物体的三种视图时,小明画出的该空心方管的主视图与俯视图分别是( )



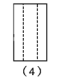 A、(1)(3) B、(1)(4) C、(2)(3) D、(2)(4)6. 如图所示,从左面看该几何体得到的平面图形是( )
A、(1)(3) B、(1)(4) C、(2)(3) D、(2)(4)6. 如图所示,从左面看该几何体得到的平面图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,是一个正方体截去一个角后得到的几何体,则该几何体的左视图是( )
7. 如图,是一个正方体截去一个角后得到的几何体,则该几何体的左视图是( )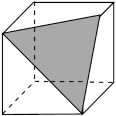 A、
A、 B、
B、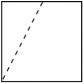 C、
C、 D、
D、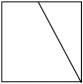 8. 如图,几何体是由六个相同的立方体构成的,则该几何体三视图中面积最大的是( )
8. 如图,几何体是由六个相同的立方体构成的,则该几何体三视图中面积最大的是( )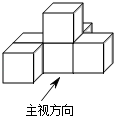 A、主视图 B、左视图 C、俯视图 D、主视图和左视图9. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、310. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图9. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、310. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )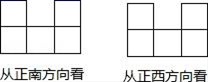 A、12个 B、13个 C、14个 D、18个
A、12个 B、13个 C、14个 D、18个二、填空题
-
11. 如图是由一些相同的小正方体搭成的几何体从左边和上面看到的形状图,搭这个几何体最少需要个小正方体,最多需要个小正方体.
 12. 已知某几何体的三视图如图所示,则该几何体的体积为 .
12. 已知某几何体的三视图如图所示,则该几何体的体积为 . 13. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,则树的高度为 .
13. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,则树的高度为 .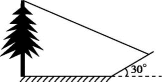 14. 如图是一个几何体的三视图,则该几何体的体积为 .
14. 如图是一个几何体的三视图,则该几何体的体积为 . 15. 如图,小树AB在路灯O的照射下形成树影BC. 若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=5m,则路灯的高度OP为 m.
15. 如图,小树AB在路灯O的照射下形成树影BC. 若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=5m,则路灯的高度OP为 m. 16. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.
16. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.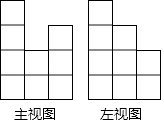
三、作图题
-
17. 如图是由小正方体搭成的一个几何体从上面着到的形状图,小正方形中的数字表示在该位置的小正方体的个数,请你画出它从正面和从左面看到的形状图.
 18. 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
18. 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
四、解答题
-
19. 如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度.
 20. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
20. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.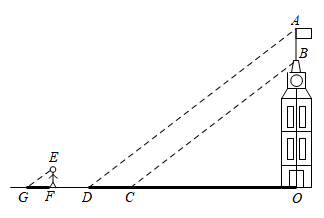 21. 据说,在距今2500多年前,古希腊数学家就已经较准确地测出了埃及金字塔的高度,操作过程大致如下:如图所示,设AB是金字塔的高,在某一时刻,阳光照射下的金字塔在底面上投下了一个清晰的阴影,塔顶A的影子落在地面上的点C处,金字塔底部可看作方正形FGHI,测得正方形边长FG长为160米,点B在正方形的中心,BC与金字塔底部一边垂直于点K,与此同时,直立地面上的一根标杆DO留下的影子是OE,射向地面的太阳光线可看作平行线(AC∥DE),此时测得标杆DO长为1.2米,影子OE长为2.7米,KC长为250米,求金字塔的高度AB及斜坡AK的坡度(结果均保留四个有效数字)
21. 据说,在距今2500多年前,古希腊数学家就已经较准确地测出了埃及金字塔的高度,操作过程大致如下:如图所示,设AB是金字塔的高,在某一时刻,阳光照射下的金字塔在底面上投下了一个清晰的阴影,塔顶A的影子落在地面上的点C处,金字塔底部可看作方正形FGHI,测得正方形边长FG长为160米,点B在正方形的中心,BC与金字塔底部一边垂直于点K,与此同时,直立地面上的一根标杆DO留下的影子是OE,射向地面的太阳光线可看作平行线(AC∥DE),此时测得标杆DO长为1.2米,影子OE长为2.7米,KC长为250米,求金字塔的高度AB及斜坡AK的坡度(结果均保留四个有效数字)
五、综合题
-
22. 用棱长都为5cm的小立方块搭成几何体,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.
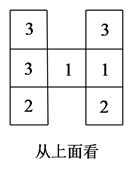 (1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;
(1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;②若新搭一个几何体,且满足如下三个条件:图中从上面看到的几何体的形状图不变,小立方块的总数不变,从上面看到的小正方形中的数字可以改变,则新搭几何体的表面积(包括与桌面接触的部分)最小值和最大值分别为 , .