人教版备考2023中考数学二轮复习 专题20 解直角三角形
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1∶ , 则AC的长是( )
 A、6米 B、12米 C、3米 D、6米2. 如图,一艘海轮位于灯塔的北偏东55°方向的处,已知海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离的长是( )
A、6米 B、12米 C、3米 D、6米2. 如图,一艘海轮位于灯塔的北偏东55°方向的处,已知海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离的长是( )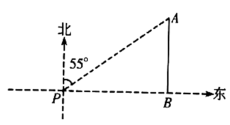 A、6海里 B、海里 C、海里 D、海里3. 一配电房示意图如图所示,它是一个轴对称图形,已知 , , 则房顶A离地面的高度为( )
A、6海里 B、海里 C、海里 D、海里3. 一配电房示意图如图所示,它是一个轴对称图形,已知 , , 则房顶A离地面的高度为( )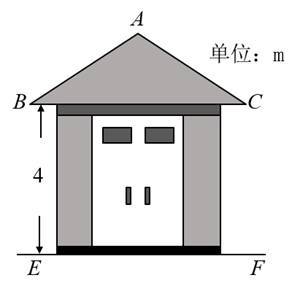 A、 B、 C、 D、4. 如图,在平面直角坐标系内,以坐标原点O为圆心的圆交x轴于A,B两点,其中A点坐标为 , 为第一象限内圆上一点,连接OP,则的值为( )
A、 B、 C、 D、4. 如图,在平面直角坐标系内,以坐标原点O为圆心的圆交x轴于A,B两点,其中A点坐标为 , 为第一象限内圆上一点,连接OP,则的值为( ) A、a B、b C、 D、5. 由12个有公共顶点O的直角三角形拼成如图所示的图形, , . 若 , 则图中与位似的三角形的面积为( )
A、a B、b C、 D、5. 由12个有公共顶点O的直角三角形拼成如图所示的图形, , . 若 , 则图中与位似的三角形的面积为( )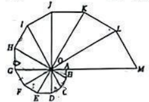 A、 B、 C、 D、6. 已知:在中, , 则BC的值( )A、只有1个 B、可以有2个 C、可以有3个 D、无数个7. 如图,在中, , , 那么下列结论正确的是( )
A、 B、 C、 D、6. 已知:在中, , 则BC的值( )A、只有1个 B、可以有2个 C、可以有3个 D、无数个7. 如图,在中, , , 那么下列结论正确的是( ) A、 B、 C、 D、8. 如图,在等边三角形ABC的AC,BC边上分别任取一点P,Q,且AP=CQ,AQ、BP相交于点O.下列四个结论:①若PC=2AP,则BO=6OP;②若BC=8,BP=7,则PC=5;③AP2=OP•AQ;④若AB=3,则OC的最小值为 , 其中正确的是( )
A、 B、 C、 D、8. 如图,在等边三角形ABC的AC,BC边上分别任取一点P,Q,且AP=CQ,AQ、BP相交于点O.下列四个结论:①若PC=2AP,则BO=6OP;②若BC=8,BP=7,则PC=5;③AP2=OP•AQ;④若AB=3,则OC的最小值为 , 其中正确的是( ) A、①②④ B、①③④ C、②③④ D、①②③9. 如图,在平面直角坐标系中,抛物线的顶点为A点,且与x轴的正半轴交于点B,P点是该抛物线对称轴上的一点,则的最小值为( )
A、①②④ B、①③④ C、②③④ D、①②③9. 如图,在平面直角坐标系中,抛物线的顶点为A点,且与x轴的正半轴交于点B,P点是该抛物线对称轴上的一点,则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 如图,△ABC的顶点都在正方形网格纸的格点上,则sinC=
 11. 在中, , 点为的中点, , 那么的长为 .12. 如图,传送带和地面所成斜坡的坡度为 , 若它把物体从地面点处送到离地面米高的处,则物体从到所经过的路程为米.
11. 在中, , 点为的中点, , 那么的长为 .12. 如图,传送带和地面所成斜坡的坡度为 , 若它把物体从地面点处送到离地面米高的处,则物体从到所经过的路程为米. 13. 如图,在中, , 点在边上,点在边上,将沿着直线翻折后,点恰好落在线段的延长线上的点处,如果 , 那么的值是 .
13. 如图,在中, , 点在边上,点在边上,将沿着直线翻折后,点恰好落在线段的延长线上的点处,如果 , 那么的值是 . 14. 已知中, , , , 那么的长是 .15. 有一块三角形材料如图所示, , , . 用这块材料剪出一个 , 其中,点D,E,F分别在 , , 上.则剪出的的面积的最大值是 .
14. 已知中, , , , 那么的长是 .15. 有一块三角形材料如图所示, , , . 用这块材料剪出一个 , 其中,点D,E,F分别在 , , 上.则剪出的的面积的最大值是 . 16. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .
16. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .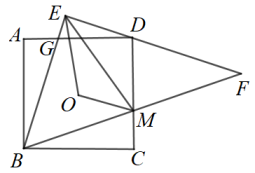 17. 图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得 , 且在 B点和点观测点的仰角均为 , 则点到桥面的距离为 , “戒指” 的半径为 .
17. 图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得 , 且在 B点和点观测点的仰角均为 , 则点到桥面的距离为 , “戒指” 的半径为 .
三、解答题
-
18. 如图,AD是△ABC中BC边上的高,且∠B=30°,∠C=45°,CD=2.求BC的长.
 19. 如图,在电线杆上的C处引拉线和固定电线杆.在离电线杆6米的B处安置测角仪(点B、E、D在同一直线上),在点A处测得电线杆上C处的仰角为 . 已知测角仪的高为米,拉线的长为6米,求测角仪底端(点B)与拉线固定点(E)之间的距离.
19. 如图,在电线杆上的C处引拉线和固定电线杆.在离电线杆6米的B处安置测角仪(点B、E、D在同一直线上),在点A处测得电线杆上C处的仰角为 . 已知测角仪的高为米,拉线的长为6米,求测角仪底端(点B)与拉线固定点(E)之间的距离. 20. 如图,燕尾槽的横断面是等腰梯形ABCD,现将一根木棒MN放置在该燕尾槽中,木棒与横断面在同一平面内,厚度等不计,它的底端N与点C重合,且经过点A.已知燕尾角∠B=54.5°,外口宽AD=180毫米,木棒与外口的夹角∠MAE=26.5°,求燕尾槽的里口宽BC(精确到1毫米).(参考数据: , , , , , )
20. 如图,燕尾槽的横断面是等腰梯形ABCD,现将一根木棒MN放置在该燕尾槽中,木棒与横断面在同一平面内,厚度等不计,它的底端N与点C重合,且经过点A.已知燕尾角∠B=54.5°,外口宽AD=180毫米,木棒与外口的夹角∠MAE=26.5°,求燕尾槽的里口宽BC(精确到1毫米).(参考数据: , , , , , )
四、综合题
-
21. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,)
 (1)、求∠ABC的度数;(2)、测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)22. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .
(1)、求∠ABC的度数;(2)、测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)22. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .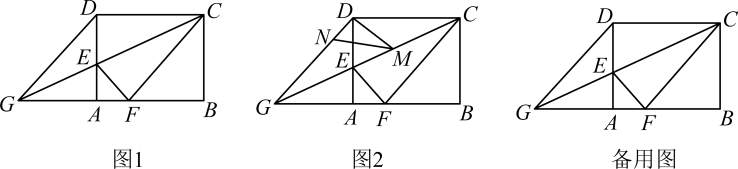 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.