人教版备考2023中考数学二轮复习 专题19 相似三角形
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 若两个相似三角形的面积之比为1:4,则它们的最长边的比是( )A、1:2 B、1:4 C、1:16 D、无法确定2. 如图示,已知 , 那么添加下列一个条件后,仍无法判定的是( )
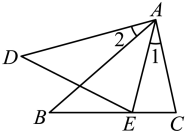 A、 B、 C、 D、3. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( )
A、 B、 C、 D、3. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( )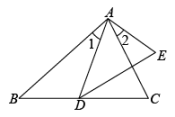 A、 B、 C、 D、4. 如图,在△ABC中,点D,E分别在AB,AC上,若DE∥BC, , AE=6cm,则AC的长为( )
A、 B、 C、 D、4. 如图,在△ABC中,点D,E分别在AB,AC上,若DE∥BC, , AE=6cm,则AC的长为( ) A、9cm B、12cm C、15cm D、18cm5. 如图所示,在△ABC中,D、E为AB、AC的中点,若 , 则四边形DBCE的面积为( )
A、9cm B、12cm C、15cm D、18cm5. 如图所示,在△ABC中,D、E为AB、AC的中点,若 , 则四边形DBCE的面积为( ) A、4 B、6 C、8 D、106. 如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AC的长为( )
A、4 B、6 C、8 D、106. 如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AC的长为( ) A、8 B、9 C、10 D、117. 如图,是半圆的直径,的平分线分别交弦和半圆于E和D,若 , , 则长为( )
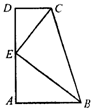
A、8 B、9 C、10 D、117. 如图,是半圆的直径,的平分线分别交弦和半圆于E和D,若 , , 则长为( ) A、2 B、 C、 D、8. 如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
A、2 B、 C、 D、8. 如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )①; ②; ③;④CE2=CD×BC; ⑤BE2=AE×BC
 A、2个 B、3个 C、4个 D、5个9. 如图,在等边三角形ABC中,点P,Q分别是AC,BC边上的动点(都不与线段端点重合),且AP=CQ,AQ、BP相交于点O.下列四个结论:①若PC=2AP,则BO=6OP;②若BC=8,BP=7,则PC=5;③AP2=OP⋅AQ;④若AB=3,则OC的最小值为 , 其中正确的是( )
A、2个 B、3个 C、4个 D、5个9. 如图,在等边三角形ABC中,点P,Q分别是AC,BC边上的动点(都不与线段端点重合),且AP=CQ,AQ、BP相交于点O.下列四个结论:①若PC=2AP,则BO=6OP;②若BC=8,BP=7,则PC=5;③AP2=OP⋅AQ;④若AB=3,则OC的最小值为 , 其中正确的是( ) A、①③④ B、①②④ C、②③④ D、①②③
A、①③④ B、①②④ C、②③④ D、①②③二、填空题
-
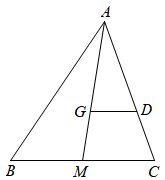
10. 如图,在中,是中线,G是重心, , 交于D.若 , 则.
 11. 已知∽ , 顶点、、分别与顶点、、对应,、分别是、边上的中线,如果 , 那么的长是 .12. 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=.
11. 已知∽ , 顶点、、分别与顶点、、对应,、分别是、边上的中线,如果 , 那么的长是 .12. 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=. 13. 如图,矩形的边在的边上,顶点、分别在边、上.已知 , , , 那么的面积是 .
13. 如图,矩形的边在的边上,顶点、分别在边、上.已知 , , , 那么的面积是 . 14. 如图,在中, , , 点P从点B开始沿边向点A以每秒的速度移动,点Q从点A开始沿边向点C以每秒的速度移动.如果P、Q分别从B、A同时出发,经过秒钟与相似?
14. 如图,在中, , , 点P从点B开始沿边向点A以每秒的速度移动,点Q从点A开始沿边向点C以每秒的速度移动.如果P、Q分别从B、A同时出发,经过秒钟与相似? 15. 如图,在矩形ABCD和矩形AEGH中,AD∶AB=AH∶AE=1∶2.则DH∶CG∶BE= .
15. 如图,在矩形ABCD和矩形AEGH中,AD∶AB=AH∶AE=1∶2.则DH∶CG∶BE= .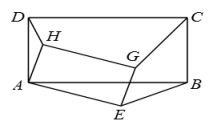 16. 如图,在正方形ABCD中,点E在边AD上,把△ABE沿直线BE翻折得到△FBE,连接CF并延长交BE的延长线于点P.若AB=5,AE=1.则∠P= , PC=.
16. 如图,在正方形ABCD中,点E在边AD上,把△ABE沿直线BE翻折得到△FBE,连接CF并延长交BE的延长线于点P.若AB=5,AE=1.则∠P= , PC=.
三、作图题
-
17. 如图是8×6的正方形网格,已知△ABC,请按下列要求完成作图(要求保留作图痕迹,不要求写作法和结论).
 (1)、将△ABC绕点C按顺时针方向旋转90°,得到△A1B1C1 , 请在图1中作出△A1B1C1.(2)、在图2中,在AC所在直线的左侧找一格点E,画∠AEC=∠B.(3)、在图3中,仅用无刻度直尺在线段AC上找一点M,使得.18. 如图,在4×8的网格中,已知格点△ABC(小正方形的顶点称为格点,顶点在格点处的三角形称为格点三角形),在图1、图2中分别画一个格点三角形(所画的两个三角形不全等),使其同时符合下列两个条件.
(1)、将△ABC绕点C按顺时针方向旋转90°,得到△A1B1C1 , 请在图1中作出△A1B1C1.(2)、在图2中,在AC所在直线的左侧找一格点E,画∠AEC=∠B.(3)、在图3中,仅用无刻度直尺在线段AC上找一点M,使得.18. 如图,在4×8的网格中,已知格点△ABC(小正方形的顶点称为格点,顶点在格点处的三角形称为格点三角形),在图1、图2中分别画一个格点三角形(所画的两个三角形不全等),使其同时符合下列两个条件. (1)、与△ABC有一公共角;(2)、与△ABC相似但不全等.
(1)、与△ABC有一公共角;(2)、与△ABC相似但不全等.四、解答题
-
19. 已知:、是的边、上的点, , , , , 求证:.
 20. 如图, , , , , , 求的长.
20. 如图, , , , , , 求的长. 21. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.
21. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.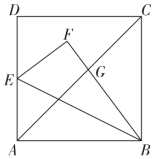 22. 如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 .
22. 如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 . (1)、求 点的坐标;(2)、设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.
(1)、求 点的坐标;(2)、设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.五、综合题
-
23. 定义:若一动点P到一条线段的两个端点的距离满足 , 则称P为线段的点,但点P不是线段的点.
 (1)、如图1,在中, , , 若点C是线段的点,求的长.(2)、如图2,在中,D是边上一点,连结 , 若点A分别是线段 , 线段的点.求证:C是线段的点(提示:证明与相似).(3)、如图3,在菱形中, , , 点E,F分别是 , 上的点,且满足.连结 , 若点E是线段的点.求的长.24. 如图1,在中, , D是斜边上一动点 , 以点A为圆心,长为半径作圆A交于点F,连结并延长交圆A于点E,连结.
(1)、如图1,在中, , , 若点C是线段的点,求的长.(2)、如图2,在中,D是边上一点,连结 , 若点A分别是线段 , 线段的点.求证:C是线段的点(提示:证明与相似).(3)、如图3,在菱形中, , , 点E,F分别是 , 上的点,且满足.连结 , 若点E是线段的点.求的长.24. 如图1,在中, , D是斜边上一动点 , 以点A为圆心,长为半径作圆A交于点F,连结并延长交圆A于点E,连结. (1)、求证:.(2)、如图2,若 , 求的长.(3)、如图3
(1)、求证:.(2)、如图2,若 , 求的长.(3)、如图3①若平分 , 求圆A的半径长;
②当点D在斜边上运动时,直接写出的最大值.
25. 如图, 四边形内接于 , 平分 , 过点D作 , 交于点E, 连结交于点F. 已知 , (1)、①假设 , 则 .
(1)、①假设 , 则 .②证明: ;
(2)、若 , 求的长;(3)、若 , 求的长.26. (1)、 【基础巩固】如图1, 在中, 分别为上的点, 交 于点G, 求证: .(2)、 【尝试应用】如图2, 已知为的边上的两点, 且满足 , 一条平行于的直线分别交和于点和 , 求 的值.(3)、 【拓展提高】如图3, 点E是正方形的边上的一个动点, , 延长至点F, 使 , 连接 , 求的最小值.27. 已知,在中, , , , 点、分别在边、上,且均不与顶点重合,(如图1所示),设 , .
(1)、 【基础巩固】如图1, 在中, 分别为上的点, 交 于点G, 求证: .(2)、 【尝试应用】如图2, 已知为的边上的两点, 且满足 , 一条平行于的直线分别交和于点和 , 求 的值.(3)、 【拓展提高】如图3, 点E是正方形的边上的一个动点, , 延长至点F, 使 , 连接 , 求的最小值.27. 已知,在中, , , , 点、分别在边、上,且均不与顶点重合,(如图1所示),设 , . (1)、当点与点重合时(如图2所示),求线段的长;(2)、在图1中当点不与点重合时,求关于的函数解析式及其定义域;(3)、我们把有一组相邻内角相等的凸四边形叫做等邻角四边形.请阅读理解以上定义,完成问题探究:如图1,设点在边上, , 如果四边形是等邻角四边形,求线段的长.
(1)、当点与点重合时(如图2所示),求线段的长;(2)、在图1中当点不与点重合时,求关于的函数解析式及其定义域;(3)、我们把有一组相邻内角相等的凸四边形叫做等邻角四边形.请阅读理解以上定义,完成问题探究:如图1,设点在边上, , 如果四边形是等邻角四边形,求线段的长.