人教版备考2023中考数学二轮复习 专题26 平移、旋转
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 点关于原点的对称点的坐标是( )A、 B、 C、 D、2. 某市实验学校的美术课上,七年级同学创造了一批民间剪纸艺术作品,下列剪纸作品中,是中心对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 3. 2020年2月11日,世卫组织在日内瓦召开发布会,宣布将新型冠状病毒肺炎正式命名为“”;“”中将每一个字母看成一个图形,那么是中心对称图形的个数为( )A、0 B、1 C、2 D、34. 如图,是由绕点旋转得到的,若 , , , 则旋转角的度数为( )
3. 2020年2月11日,世卫组织在日内瓦召开发布会,宣布将新型冠状病毒肺炎正式命名为“”;“”中将每一个字母看成一个图形,那么是中心对称图形的个数为( )A、0 B、1 C、2 D、34. 如图,是由绕点旋转得到的,若 , , , 则旋转角的度数为( ) A、80° B、50° C、40° D、10°5. 如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为( )
A、80° B、50° C、40° D、10°5. 如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为( ) A、(3,-2) B、(3,-1) C、(2,-3) D、(3,2)6. 如图,在中, , 将绕点按逆时针方向旋转得 , 且点在上,交于点 , 则的度数为
A、(3,-2) B、(3,-1) C、(2,-3) D、(3,2)6. 如图,在中, , 将绕点按逆时针方向旋转得 , 且点在上,交于点 , 则的度数为 ( )
( )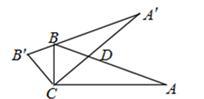 A、 B、 C、 D、7. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( )
A、 B、 C、 D、7. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ) A、25° B、30° C、35° D、40°8. 如图,将绕直角顶点C顺时针旋转 , 得 , 连接 , 若 , 则的大小为( )
A、25° B、30° C、35° D、40°8. 如图,将绕直角顶点C顺时针旋转 , 得 , 连接 , 若 , 则的大小为( ) A、 B、 C、 D、9. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为( )
A、 B、 C、 D、9. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为( )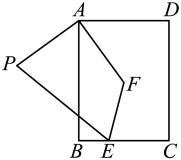 A、 B、 C、4 D、10. 如图,O是正内一点, , , , , 将线段BO以点B为旋转中心逆时针旋转60°得到线段 , 下列结论:①点O与的距离为6;②;③;④;⑤点P为内一点,则点P到三个顶点的距离和最小为.其中正确的结论是( )
A、 B、 C、4 D、10. 如图,O是正内一点, , , , , 将线段BO以点B为旋转中心逆时针旋转60°得到线段 , 下列结论:①点O与的距离为6;②;③;④;⑤点P为内一点,则点P到三个顶点的距离和最小为.其中正确的结论是( ) A、①②③⑤ B、①③④ C、②③④⑤ D、①②⑤
A、①②③⑤ B、①③④ C、②③④⑤ D、①②⑤二、填空题
-
11. 在平面直角坐标系中,点A坐标为(5,-4),连接OA,将OA绕点O旋转后,得到OB,则点B的坐标为 .12. 已知点A的坐标为 , O为坐标原点,连接 , 将线段绕点O按逆时针方向旋转90°得 , 则点的坐标为.13. 如图,将△ABC绕着点C顺时针旋转50°后得到△A’B’C.若=40°,=110°,则∠的度数为.
 14. 如图,已知点 , , , , 连接 , . 将线段绕着某一点旋转一定角度,使其与线段重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .
14. 如图,已知点 , , , , 连接 , . 将线段绕着某一点旋转一定角度,使其与线段重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .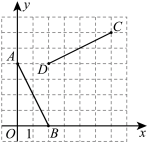 15. 如图,在平面直角坐标系中,点A在y轴的正半轴上, , 将绕点O顺时针旋转到 , 扫过的面积记为 , 交x轴于点;将绕点O顺时针旋转到 , 扫过的面积记为 , 交y轴于点;将绕点O顺时针旋转到 , 扫过的面积记为 , 交x轴于点;…;按此规律,则的值为 .
15. 如图,在平面直角坐标系中,点A在y轴的正半轴上, , 将绕点O顺时针旋转到 , 扫过的面积记为 , 交x轴于点;将绕点O顺时针旋转到 , 扫过的面积记为 , 交y轴于点;将绕点O顺时针旋转到 , 扫过的面积记为 , 交x轴于点;…;按此规律,则的值为 . 16. 如图,等边△ABC内有一点O,OA=3,OB=4,OC=5,以点B为旋转中心将BO逆时针旋转60°得到线段 , 连接 , 下列结论:①可以看成是△BOC绕点B逆时针旋转60°得到的;②点O与的距离为5;③∠AOB=150°;④S四边形AOBO′=6+4;⑤=6+ . 其中正确的结论有 . (填正确序号)
16. 如图,等边△ABC内有一点O,OA=3,OB=4,OC=5,以点B为旋转中心将BO逆时针旋转60°得到线段 , 连接 , 下列结论:①可以看成是△BOC绕点B逆时针旋转60°得到的;②点O与的距离为5;③∠AOB=150°;④S四边形AOBO′=6+4;⑤=6+ . 其中正确的结论有 . (填正确序号)
三、作图题
-
17. 如图,正方形网格的每个小正方形边长都是1,每个小正方形的顶点叫做格点. 的三个顶点A,B,C都在格点上,现将绕点A按逆时针方向旋转得到.
 (1)、在正方形网格中画出.(2)、计算线段在变换到的过程中扫过区域的面积.18. 已知在平面直角坐标系中的位置如图所示.将向右平移6个单位长度,再向下平移6个单位长度得到图中每个小方格边长均为1个单位长度 .
(1)、在正方形网格中画出.(2)、计算线段在变换到的过程中扫过区域的面积.18. 已知在平面直角坐标系中的位置如图所示.将向右平移6个单位长度,再向下平移6个单位长度得到图中每个小方格边长均为1个单位长度 . (1)、在图中画出平移后的;(2)、直接写出各顶点的坐标.
(1)、在图中画出平移后的;(2)、直接写出各顶点的坐标.四、解答题
-
19. 如图,将绕点A逆时针旋转得到 . 使点B的对应点E落在边上,求的度数.
 20. 如图,将矩形绕点A顺时针旋转得到矩形 , 点C的对应点恰好落在的延长线上,求证: .
20. 如图,将矩形绕点A顺时针旋转得到矩形 , 点C的对应点恰好落在的延长线上,求证: .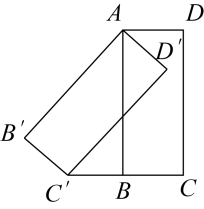 21. 如图,在Rt△ABC中,∠BAC=90°,AB=AC.点D是△ABC内的一点,连接AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连接BD、CE.求证:BD=CE.
21. 如图,在Rt△ABC中,∠BAC=90°,AB=AC.点D是△ABC内的一点,连接AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连接BD、CE.求证:BD=CE.
五、综合题
-
22. 如图,四边形是正方形,连接 , 将绕点A逆时针旋转α得到 , 连接 , O为的中点,连接.
 (1)、如图1,当时,求证:.(2)、如图2,当时,(1)中的结论还成立吗?请说明理由.23. 问题情境
(1)、如图1,当时,求证:.(2)、如图2,当时,(1)中的结论还成立吗?请说明理由.23. 问题情境在综合实践课上,老师组织兴趣小组开展数学活动,探究正方形的旋转问题.在正方形和正方形中,点G,A,B在一条直线上,连接(如图1).
 (1)、操作发现
(1)、操作发现
图1中线段和的数量关系是 , 位置关系是 .(2)、在图1的基础上,将正方形绕着点A沿顺时针方向旋转,如图2所示,(1)中的结论是否成立?请仅就图2的情况说明理由.(3)、类比探究
如图3,若将图2中的正方形和正方形都变为矩形,且 , 请仅就图3的情况探究与之间的数量关系.