人教版备考2023中考数学二轮复习 专题25 轴对称
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘以-1,所得图形与原图形的关系是( )A、关于轴对称 B、关于轴对称 C、关于原点对称 D、无法确定2. 在平面直角坐标系中,点与点关于轴对称,则的值为( )A、-3 B、-2 C、1 D、23. 如图,在中, , 平分 , 点E是的中点,点P是上一动点,连接 , 若 , , , 则的最小值是( )
 A、 B、6 C、 D、104. 下列LOGO中,是轴对称图形的是( )A、
A、 B、6 C、 D、104. 下列LOGO中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列语句中,正确的有( )
5. 下列语句中,正确的有( )相等的圆心角所对的弧相等;等弦对等弧;平分弦的直径垂直于弦;经过圆心的每一条直线都是圆的对称轴.
A、1个 B、2个 C、3个 D、4个6. 如图,将半径为8的沿折叠,弧恰好经过与垂直的半径的中点 , 则折痕长为( ) A、 B、 C、8 D、107. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )
A、 B、 C、8 D、107. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )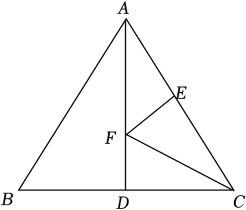 A、30° B、45° C、25° D、20°8. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( )
A、30° B、45° C、25° D、20°8. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( ) A、7 B、8 C、9 D、109. 如图,A点是半圆上一个三等分点,B点是弧AN的中点,P点是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值为( )
A、7 B、8 C、9 D、109. 如图,A点是半圆上一个三等分点,B点是弧AN的中点,P点是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值为( ) A、1 B、 C、 D、10. 如图,是边长为2的等边三角形,的面积等于 , D,E分别为 , 的中点,P是上的一个动点,则的最小值为( )
A、1 B、 C、 D、10. 如图,是边长为2的等边三角形,的面积等于 , D,E分别为 , 的中点,P是上的一个动点,则的最小值为( ) A、 B、 C、1 D、2
A、 B、 C、1 D、2二、填空题
-
11. 点关于轴对称的点坐标是 .12. 从如图的四张印有品牌标志图案的卡片中任取一张,取出印有品牌标志的图案是轴对称图形的卡片的概率是 .
 13. 在中, , 为边上一点,将三角形沿折叠,使落在边上,点与点重合,若为直角三角形,则的度数为.
13. 在中, , 为边上一点,将三角形沿折叠,使落在边上,点与点重合,若为直角三角形,则的度数为.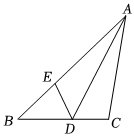 14. 在Rt△ABC中,∠B=90°,AB=4,BC=8,D、E分别是边AC、BC上的点,将△ABC沿着DE进行翻折,点A和点C重合,则EC=.
14. 在Rt△ABC中,∠B=90°,AB=4,BC=8,D、E分别是边AC、BC上的点,将△ABC沿着DE进行翻折,点A和点C重合,则EC=. 15. 如图,在Rt△ABC中,∠A=90°,AB=12,AC=5,M、N、P分别是边AB、AC、BC上的动点,连接PM、PN和MN,则PM+PN+MN的最小值是 .
15. 如图,在Rt△ABC中,∠A=90°,AB=12,AC=5,M、N、P分别是边AB、AC、BC上的动点,连接PM、PN和MN,则PM+PN+MN的最小值是 .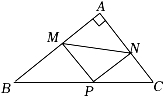 16. 如图,在矩形中, , , 、分别是边、上一点, , 将沿翻折得 , 连接 , 当 时,是以为腰的等腰三角形.
16. 如图,在矩形中, , , 、分别是边、上一点, , 将沿翻折得 , 连接 , 当 时,是以为腰的等腰三角形.
三、作图题
-
17. 如图,阴影部分是由4个小正方形组成的“”形,请用二种方法分别在如图的空白方格内涂黑一个小正方形,使阴影部分成为轴对称图形.
 18. 如图,三个顶点的坐标分别是 ,
18. 如图,三个顶点的坐标分别是 ,
( 1 )请画出向左平移6个单位后得到的 , 并写出的坐标;
( 2 )请画出关于原点对称的 , 并写出点的坐标;
( 3 )在x轴上求一点P使周长最小(保留作图痕迹,不写作法)
四、解答题
-
19. 根据以下素材,探索完成任务.
如何确定箭头形指示牌?
素材1
某校计划在校园里立一块如图1所示的指示牌,图2为其平面设计图.该指示牌是轴对称图形,由长方形EFHD和三角形ABC组成,且点B,F,E,C四点共线.小聪测量了点A到DH的距离为2.7米,DH=0.8米,DE=1.5米.

素材2
因考虑牢固耐用,小聪打算选用甲、乙两种材料分别制作长方形与三角形(两种图形无缝隙拼接),且甲材料的单价为每平方米85元,乙材料的单价为每平方米100元.

问题解决
任务1
推理最大高度
小聪说:“如果我设计的方案中CB长与C,D两点间的距离相等,那么最高点B到地面的距离就是线段DE长”,他的说法对吗?请判断并说明理由.
任务2
确定箭头形指示牌
小聪发现他设计的方案中,制作广告牌的总费用不超过180元,请你确定CE长度的最大值.
20. 如图是由16个小正方形组成的正方形网格图,现已将其中的两个涂黑.请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形,使整个图形成为轴对称图形. 21. 如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是 , 高为 . 它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角 , 发现并证明了点在上.请你继续完成长的计算.
21. 如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是 , 高为 . 它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角 , 发现并证明了点在上.请你继续完成长的计算.参考数据: , , , , , .

五、综合题
-
22. 我们定义:最大边与最小边的比为5:3的三角形叫做“型三角形”,最长边称为“弦边”.
 (1)、小张认为:等腰三角形不可能是“型三角形”你认为他的说法正确吗?若正确,请说明理由;若不正确,请举出反例;(2)、若是“型三角形”, , “弦边” , 则;(3)、如图,在中, , 现将关于直线作轴对称,点的对称点为点 , 连结 , 作 , 垂足为当是“型三角形”时,求线段的长.23. 在平面直角坐标系中,已知为坐标原点,点 , . 以点为旋转中心,把顺时针旋转,得 .
(1)、小张认为:等腰三角形不可能是“型三角形”你认为他的说法正确吗?若正确,请说明理由;若不正确,请举出反例;(2)、若是“型三角形”, , “弦边” , 则;(3)、如图,在中, , 现将关于直线作轴对称,点的对称点为点 , 连结 , 作 , 垂足为当是“型三角形”时,求线段的长.23. 在平面直角坐标系中,已知为坐标原点,点 , . 以点为旋转中心,把顺时针旋转,得 . (1)、如图①,当旋转后满足轴时,求点C的坐标;(2)、如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标;(3)、在(2)的条件下,边OB上的一点旋转后的对应点为当取得最小值时,求点的坐标(直接写出结果即可).
(1)、如图①,当旋转后满足轴时,求点C的坐标;(2)、如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标;(3)、在(2)的条件下,边OB上的一点旋转后的对应点为当取得最小值时,求点的坐标(直接写出结果即可).