人教版备考2023中考数学二轮复习 专题24 命题与证明
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 下列说法正确的是( )A、1是最小的正数 B、-1是最大的负数 C、绝对值等于本身的数是0 D、0既不是正数也不是负数2. 下列语句是命题的是( )A、作直线AB的垂线 B、在线段AB上取点C C、垂线段最短吗? D、同旁内角互补3. 下列命题是假命题的是( )A、是最简二次根式 B、若点在直线 , 则 C、三角形的外角一定大于它的内角 D、同旁内角互补,两直线平行4. 下列选项中,能说明命题“若a≤1,则a2≤1”是假命题的反例是( )A、a=2 B、a=1 C、a=-1 D、a=-25. 期末考试中出现了如图所示的一道题,小明同学从中任选了两个选项(每一个选项被选中的机会均等),请问小明答对题的概率是( )
(不定项选择题)下列选项中,正确的有( )
A.抛掷一枚硬币两次,出现一次正面、一次反面是必然事件
B.与是同类二次根式
C.直角三角形斜边上的中线等于斜边的一半
D.相似三角形的周长之比等于相似比
A、 B、 C、 D、6. 以下命题:①每条直径都是所在圆的对称轴;②长度相等的弧是等弧;③相等的弦所对的弧也相等;④圆内接四边形对角互补.其中真命题的个数是( )A、0 B、1 C、2 D、37. 下列命题属于假命题的是( )A、全等三角形的对应边相等 B、全等三角形的对应角相等 C、三条边对应相等的两个三角形全等 D、三个角对应相等的两个三角形全等8. 对于一元二次方程(a≠0),下列命题中错误的是( )A、a+b+c=0,则 B、若方程有两个不相等的实根,则方程必有两个不相等的实根 C、若c是方程的一个根,则一定有ac+b+1=0成立 D、若x0是一元二次方程的根,则9. 如图, , 点D在BC边上, , EC、ED与AB交于点F、G,则下列结论不正确的是( )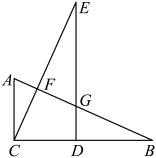 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 定理“直角三角形的两个锐角互余”的逆定理是 .11. 在说明命题“若|a|>3,则a>3”是假命题的反例中,a的值可以是 .12. 命题“如果|a|=|b|,那么a2=b2”的逆命题是 , 此命题是(选填“真“或“假”)命题.13. 请举反例说明命题“若 , 则”是假命题,你举的反例是 .14. 有同样大小的三个立方体骰子,每个骰子的展开图如图1所示,现在把三个股子放在桌子上(如图2),凡是能看得到的点数之和最大是 , 最小是 .
 15. 为鼓励学生居家锻炼,李老师组织线上仰卧起坐接力活动.4人为一组,每人自主设定个人目标(单位:次),组内任意2人之间均需接力一场,且每场接力2人都达到个人目标即停止,记录每场接力成绩(2人所做仰卧起坐次数之和).小贾、小易、小冰、小丁为一组,他们六场接力成绩由小到大依次为86,92,94,98,100,106.若他们设定的个人目标分别记为a,b,c,d,其中 , 且 . 根据以上信息,得到三个结论:① , ;②六场接力成绩由小到大可以依次表示为: , , , , , ;③a,b,c,d的值分别为46,40,52,54.其中正确结论的序号是 .
15. 为鼓励学生居家锻炼,李老师组织线上仰卧起坐接力活动.4人为一组,每人自主设定个人目标(单位:次),组内任意2人之间均需接力一场,且每场接力2人都达到个人目标即停止,记录每场接力成绩(2人所做仰卧起坐次数之和).小贾、小易、小冰、小丁为一组,他们六场接力成绩由小到大依次为86,92,94,98,100,106.若他们设定的个人目标分别记为a,b,c,d,其中 , 且 . 根据以上信息,得到三个结论:① , ;②六场接力成绩由小到大可以依次表示为: , , , , , ;③a,b,c,d的值分别为46,40,52,54.其中正确结论的序号是 .三、解答题
-
16. 把下面的说理过程补充完整:
已知:如图,在四边形中, , 直线与和的延长线分别交于点 , , 若 , 那么与相等吗?请说明理由.
解: . 理由如下:
因为(已知),
所以 ▲ ▲ ( ),
所以 ▲ ( ),
因为 ▲ (已知),
所以 ▲ ( ),
所以(等量代换).
 17. 如图,在长方形中, , 垂直平分分别交 , 于 , , 求证: . (请你将下面的推理过程中的横线空白处补充完整.)
17. 如图,在长方形中, , 垂直平分分别交 , 于 , , 求证: . (请你将下面的推理过程中的横线空白处补充完整.)
解:∵( )
∴( )
∵垂直平分(已知)
∴(线段垂直平分线的定义)
在和中,
,
∴( )
∴( )
又∵垂直平分(已知)
∴ ▲ (线段垂直平分线上的点到线段两端的距离相等)
∴( ).
四、综合题

