人教版备考2023中考数学二轮复习 专题22 圆
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 下列语句中不正确的有( )
①长度相等的弧是等弧;②垂直于弦的直径平分弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④平分弦的直线也必平分弦所对的两条弧;⑤半圆是圆中最长的弧;⑥不在同一条直线上的三个点可以确定一个圆.
A、5个 B、4个 C、3个 D、2个2. 如图,为了美化校园,学校在一块边角空地建造了一个扇形花圃,扇形圆心角∠AOB=120°,半径OA为3m,那么花圃的面积为( ) A、6πm2 B、3πm2 C、2πm2 D、πm23. 如图,半圆O的直径 , 弦 , 弦平分 , 的长为( )
A、6πm2 B、3πm2 C、2πm2 D、πm23. 如图,半圆O的直径 , 弦 , 弦平分 , 的长为( ) A、 B、 C、 D、4. 如图,四边形内接于 , 交的延长线于点E,若平分 , , , 则( )
A、 B、 C、 D、4. 如图,四边形内接于 , 交的延长线于点E,若平分 , , , 则( )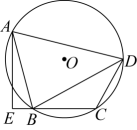 A、3 B、 C、 D、5. 如图,是的直径, , 是上位于两侧的点,若 , 则度数为( )
A、3 B、 C、 D、5. 如图,是的直径, , 是上位于两侧的点,若 , 则度数为( ) A、 B、 C、 D、6. 已知⊙O的半径为3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法确定7. 如图所示,已知矩形的边若以点A为圆心作 , 使三点中至少有一个点在圆内,且至少有一点在圆外,则的半径r的取值范围是( )
A、 B、 C、 D、6. 已知⊙O的半径为3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法确定7. 如图所示,已知矩形的边若以点A为圆心作 , 使三点中至少有一个点在圆内,且至少有一点在圆外,则的半径r的取值范围是( ) A、 B、 C、 D、8. 如图,为的直径,C是上的一点,若 , , 则的长度为( )
A、 B、 C、 D、8. 如图,为的直径,C是上的一点,若 , , 则的长度为( ) A、 B、 C、 D、9. 如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )
A、 B、 C、 D、9. 如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )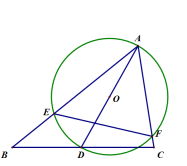 A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小10. 如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )
A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小10. 如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )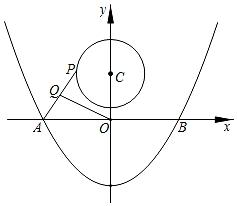 A、3 B、 C、 D、4
A、3 B、 C、 D、4二、填空题
-
11. 已知的半径为1,则它的内接正三角形边心距为 .12. 一根排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=12,如果再注入一些水,当水面AB的宽变为16时,则水面AB上升的高度为。
 13. 如图,是的弦,C是的中点,交于点D.若cm, cm,则的半径为 cm.
13. 如图,是的弦,C是的中点,交于点D.若cm, cm,则的半径为 cm. 14. 如图,直线 , , 与分别相切于点D,E,F,若 , , , 则 . (用含、的式子表示)
14. 如图,直线 , , 与分别相切于点D,E,F,若 , , , 则 . (用含、的式子表示) 15. 如图1,筒车是我国古代发明的一种水利灌溉工具,筒车盛水筒的运行轨迹是以O为圆心的一个圆,可简化为图2.若被水面所截的弦长米,的半径为米,则筒车最低点距水面米.
15. 如图1,筒车是我国古代发明的一种水利灌溉工具,筒车盛水筒的运行轨迹是以O为圆心的一个圆,可简化为图2.若被水面所截的弦长米,的半径为米,则筒车最低点距水面米. 16. 如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于的处且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的周长为 .
16. 如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于的处且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的周长为 . 17. 如图,点 , 点和点在上, , 的度数为 , 的半径为2, , 点与点在直线的两侧,交于点 , 当时, , .
17. 如图,点 , 点和点在上, , 的度数为 , 的半径为2, , 点与点在直线的两侧,交于点 , 当时, , . 18. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.
18. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.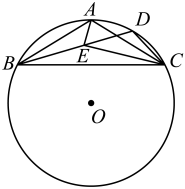
三、作图题
-
19. 如图,在中,已知.
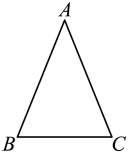 (1)、尺规作图;画的外接圆(保留作图痕迹,不写画法),(2)、连接若 , 求扇形的面积.
(1)、尺规作图;画的外接圆(保留作图痕迹,不写画法),(2)、连接若 , 求扇形的面积.四、解答题
-
20. 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
 21. 如图,的弦的相交于点 , 且.
21. 如图,的弦的相交于点 , 且.求证:.
 22. 已知是的直径,点在上,为的中点.
22. 已知是的直径,点在上,为的中点.
(Ⅰ)如图 , 连接 , , 求证:;
(Ⅱ)如图2,过点作交于点 , 直径交于点 , 若为中点,的半径为2,求的长.
五、综合题
-
23. 如图,四边形内接于为对角线, , 直径交于点F,连接 .
 (1)、如图1,求证:;(2)、如图2,连接交于点G, , 求证:;(3)、如图3,在(2)的条件下,过点G作于H,过点A作交于点M,若 , , 求线段的长.24. 如图1, , 是半圆上的两点,若直径上存在一点 , 满足 , 则称是的“幸运角”.
(1)、如图1,求证:;(2)、如图2,连接交于点G, , 求证:;(3)、如图3,在(2)的条件下,过点G作于H,过点A作交于点M,若 , , 求线段的长.24. 如图1, , 是半圆上的两点,若直径上存在一点 , 满足 , 则称是的“幸运角”. (1)、如图2,是的直径,弦 , 是上一点,连结交于点 , 连结 , 是的“幸运角”吗?请说明理由;(2)、设的度数为 , 请用含的式子表示的“幸运角”度数;(3)、在(1)的条件下,直径 , 的“幸运角”为.
(1)、如图2,是的直径,弦 , 是上一点,连结交于点 , 连结 , 是的“幸运角”吗?请说明理由;(2)、设的度数为 , 请用含的式子表示的“幸运角”度数;(3)、在(1)的条件下,直径 , 的“幸运角”为.①如图3,连结 , 求弦的长;
②当时,求的长.
25. 如图1,圆的两条弦、交于点 , 两条弦所成的锐角或者直角记为. (1)、点点同学通过画图和测量得到以下近似数据:
(1)、点点同学通过画图和测量得到以下近似数据:的度数
的度数
的度数
猜想:、、的度数之间的等量关系,并说明理由.
(2)、如图2,若 , , , 将以圆心为中心顺时针旋转,直至点与点重合,同时落在圆上的点,连接.
①求的度数;
②求.
26. 在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧. (1)、如图1,当k=1时,直接写出A,B两点的坐标;(2)、在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)、如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
(1)、如图1,当k=1时,直接写出A,B两点的坐标;(2)、在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;(3)、如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
-