人教版备考2023中考数学二轮复习专题21 四边形

试卷更新日期：2023-01-05 类型：二轮复习

进入出卷网下载

一、单选题

1. 若从 $n$ 边形的一个顶点出发，可以画出 $4$ 条对角线，则 $n$ 的值是（）

A、 $4$ B、 $5$ C、 $6$ D、 $7$

查看试题解析
2. 正五边形每个外角的度数是（）

A、144° B、108 C、72° D、36°

查看试题解析
3. 下列各式中不能表示图中阴影部分面积的是（）

A、 $3 (x + 2) + x^{2}$ B、 $x^{2} + 5 x$ C、 $(x + 3) (x + 2) - 2 x$ D、 $x (x + 3) + 6$

查看试题解析
4. 如图，扇形 $A O B$ 圆心角为直角， $O A = 10$ ，点C在 $\overset{⌢}{A B}$ 上，以 $O A$ ， $C A$ 为邻边构造 $▱ A C D O$ ，边 $C D$ 交 $O B$ 于点E，若 $O E = 8$ ，则图中两块阴影部分的面积和为（　　）

A、 $10 π - 8$ B、 $5 π - 8$ C、 $25 π - 64$ D、 $50 π - 64$

查看试题解析
5. 如图，在菱形 $A B C D$ 中， $A C = 6 c m ， B D = 8 c m$ ，则菱形 $A B C D$ 的周长是（）

A、 $14 c m$ B、 $16 c m$ C、 $18 c m$ D、 $20 c m$

查看试题解析
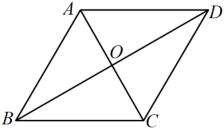6. 如图，有两个正方形纸板A，B，纸板A与B的面积之和为34．现将纸板B按甲方式放在纸板A的内部，阴影部分的面积为4．若将纸板A，B按乙方式并列放置后，构造新的正方形，则阴影部分的面积为（　　）

A、30 B、32 C、34 D、36

查看试题解析
7. 如图，在▱ABCD中，AD＝BD，∠ADC＝105°，点E在AD上，∠EBA＝60°，则 $\frac{E D}{A E}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
8. 如图1，以直角三角形的各边分别向外作正方形，再把较小的两个正方形按图2的方式放置在大正方形内，记四边形ABCD的面积为S₁ ，四边形DCEG的面积为S₂.四边形HGFP的面积为S₃ ， △GEF面积为S₄ ，若知道图中阴影部分的面积，则一定能求出（）

A、S₁ B、S₂ C、S₃ D、S₄

查看试题解析
9. 如图，四边形 $A B C D$ 和四边形 $A E F C$ 是两个矩形，点B在 $E F$ 边上，若 $A B = 2 ， A C = 3$ ，则矩形 $A E F C$ 的面积为（）

A、3 B、 $2 \sqrt{5}$ C、 $4 \sqrt{5}$ D、6

查看试题解析
10. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G，连结BG，若大正方形的面积是小正方形面积的5倍，则 $\frac{B G}{B E}$ 的值为（）

A、 $\sqrt{5}$ B、3 C、 $\sqrt{13}$ D、4

查看试题解析
11. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连结OE，∠ADC＝60°，AB＝ $\frac{1}{2}$ BC＝1.

有下列结论：①∠CAD＝30°；②BD＝ $\sqrt{7}$ ；③S_{平行四边形ABCD}＝AB·AC；④OE＝ $\frac{1}{4}$ AD；⑤S_△APO＝ $\frac{\sqrt{3}}{12}$ .其中正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

12. 在矩形 $A B C D$ 中，作 $∠ B$ 的平分线交直线 $A D$ 于点E，则 $∠ B E D$ 是度．

查看试题解析
13. 将两块全等的直角三角板如图放置，其中一块三角板的斜边恰好经过另一块三角板的直角顶点 $O$ 及斜边上的中点 $A$ ，若这两块三角板的斜边长为 $13.6 c m$ ，则 $O A =$ .

查看试题解析
14. 矩形ABCD中，AB＝5，BC＝4，点E是AB边上一点，AE＝3，连接DE，点F是BC延长线上一点，连接AF，且∠F＝ $\frac{1}{2}$ ∠EDC，则BF＝.

查看试题解析
15. 如图，在长方形ABCD中，BC＝4，CD＝2，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段AE的长为 .

查看试题解析
16. 如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD＝2∠ACB.若DG＝4，EC＝1，则DE的长为.

查看试题解析
17. 如图，梯形ABCD中，∠ABC＝∠BCD，AD∥BC，BD平分∠ABC，若AD＝3，BC＝7，则BD的长为 .

查看试题解析
18. 如图，在平行四边形 $A B C D$ 中，点E是 $B C$ 边上一点，连接 $A E 、 B D$ 交于点F，若 $∠ D A F = ∠ A B D$ ， $\frac{A F}{F E} = \frac{3}{2}$ ， $B E = \sqrt{15}$ ，则 $D F$ 的长是.

查看试题解析
19. 如图，在正方形 $A B C D$ 中，点E在 $B C$ 上，点F在 $C D$ 上， $A F ⊥ D E$ 于点M，点H在 $E M$ 上， $M H = M D$ ，连接 $A H$ 延长交 $B C$ 于点G，若 $C F = 6 ， C G = 7$ ，则线段 $D E$ 的长为．

查看试题解析

三、作图题

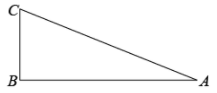
20. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ．作出点D，使四边形 $A B C D$ 是矩形．（要求：尺规作图，不写作法，保留作图痕迹）

查看试题解析
21. 如图为 $4 \times 4$ 方格，每个小正方形的边长都为1．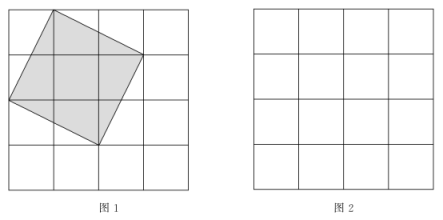

(1)、图1中阴影正方形的面积为，边长为；

(2)、请在图2中画出一个与图1中阴影部分面积不相等的正方形，并求出所画正方形的边长．要求所画正方形满足以下条件：①正方形的边长为无理数 ②正方形的四个顶点均在网格格点处．

查看试题解析

四、解答题

22. 如图，在 $▱ A B C D$ 中， $D E ⊥ A B ， D F ⊥ B C ， D E = D F$ ．求证： $▱ A B C D$ 是菱形．

查看试题解析
23. 如图，正方形 $A B C D$ 与正方形 $C E F G$ 的面积之差是6，求阴影部分的面积．

查看试题解析

24. 根据以下素材，探索完成任务.

如何设计高架桥的限高及车道宽方案？
素材1	图1高架桥是一段圆弧拱形结构，图2是它的示意图.经测量，拱形跨度24m，拱顶离地面6m.
素材2	如图3，某道路规划部门计划将左侧公路分为非机动车道、机动车道一、机动车道二及绿化带四部分，原计划设计非机动车道宽3m，每条机动车道宽均3.5m.为了保证车辆的行驶安全，高架下方需要设置限高标志以警示车辆驾驶员.（限高即图中FC的高度）
素材3	如图4，由于城市道路绿化需求，道路规划部门确定新方案为在非机动车道和机动车道一之间增加一条宽为1m的绿化带，中间绿化带宽度不变，每条机动车道道宽均不小于3.25m且相等，非机动车道最高高度不小于2.5m.
	问题解决
任务1	确定桥拱所在圆弧的半径.	在图2中补好图形，标注字母、数据等信息，求出桥拱所在圆弧的半径长.
任务2	探究原计划该高架桥下方机动车道一的限高要求.	在图3中画出图形，标注字母、数据等信息，计算确定机动车道一的限高高度.
任务3	拟定新方案下非机动车道和机动车车道宽度.	给出一对符合新方案要求的非机动车道和机动车道的道宽值. （参考数值： $\sqrt{92.75}$ ＝9.63， $\sqrt{134.75}$ ＝11.61）

查看试题解析

25. 如图，△ABC中，CD、BE分别是高，M、N分别是线段BC、DE的中点．求证：MN⊥DE.

查看试题解析

五、综合题

26. 如图①所示，将一个边长为2的正方形 $A B C D$ 和一个长为2、宽为1的长方形 $C E F D$ 拼在一起，构成一个大的长方形 $A B E F$ ．现将小长方形 $C E F D$ 绕点C顺时针旋转至长方形 $C E^{'} F^{'} D^{'}$ ，旋转角为 $α$ ．

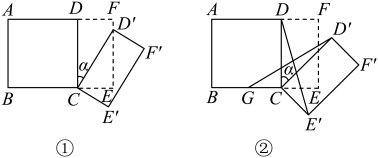(1)、当点 $D^{'}$ 恰好落在 $E F$ 边上时，求旋转角 $α$ 的值；

(2)、如图②，G为 $B C$ 中点，且 $0 ° < α < 90 °$ ，求证： $G D^{^{'}} = E^{^{'}} D$ ；

(3)、小长方形 $C E F D$ 绕点C顺时针旋转一周的过程中， $△ D C D^{'}$ 与 $△ C B D^{'}$ 能否全等？若能，直接写出旋转角 $α$ 的值；若不能，说明理由．

查看试题解析
27.

(1)、如图1，四边形 $A B C D$ 是正方形，点E是 $A D$ 边上的一个动点，以 $C E$ 为边在 $C E$ 的右侧作正方形 $C E F G$ ，连接 $D G 、 B E$ ，判断线段 $D G$ 与 $B E$ 的数量关系并说明理由；

(2)、如图2，四边形 $A B C D$ 是矩形， $A B = 3 ， B C = 6$ ，点E是 $A D$ 边上的一个动点，以 $C E$ 为边在 $C E$ 的右侧作矩形 $C E F G$ ，且 $C G ： C E = 1 ： 2$ ，连接 $D G 、 B E$ ．判断线段 $D G$ 与 $B E$ 又有怎样的数量关系，并说明理由；

(3)、如图3，在（2）的条件下，连接 $B G$ ，求 $2 B G + B E$ 的最小值．

查看试题解析

人教版备考2023中考数学二轮复习 专题21 四边形

一、单选题

二、填空题

三、作图题

四、解答题

五、综合题

人教版备考2023中考数学二轮复习专题21 四边形