人教版备考2023中考数学二轮复习 专题17 三角形
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 已知在中, , , 则的度数是( )A、 B、 C、 D、2. 已知三角形的两边长分别是5cm和10cm,则下列长度的线段中能作为第三边的是( )A、4cm B、5cm C、10cm D、15cm3. 观察下列图案,其中与如图全等的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,在中, , 若 , 则的度数为( )
4. 如图,在中, , 若 , 则的度数为( ) A、 B、 C、 D、5. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度 , 将它往前推至处时(即水平距离),踏板离地的垂直高度 , 它的绳索始终拉直,则绳索的长是( )
A、 B、 C、 D、5. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度 , 将它往前推至处时(即水平距离),踏板离地的垂直高度 , 它的绳索始终拉直,则绳索的长是( ) A、 B、 C、6 D、6. 如图,在Rt和Rt中, , , BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N, . 有下列结论:①;②;③;④≌ . 其中正确结论的个数是( ).
A、 B、 C、6 D、6. 如图,在Rt和Rt中, , , BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N, . 有下列结论:①;②;③;④≌ . 其中正确结论的个数是( ).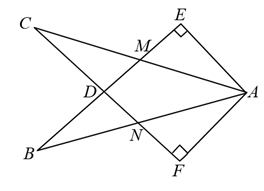 A、1个 B、2个 C、3个 D、4个7. 如图,已知 , , , 则的度数为( )
A、1个 B、2个 C、3个 D、4个7. 如图,已知 , , , 则的度数为( ) A、 B、 C、 D、8. 如图所示 , , , 点 , , 在一条直线上,若 , , 则的长为( )
A、 B、 C、 D、8. 如图所示 , , , 点 , , 在一条直线上,若 , , 则的长为( )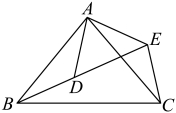 A、2 B、5 C、8 D、159. 如图,在的正方形方格中,每个小正方形方格的边长都为1,则和的关系是( )
A、2 B、5 C、8 D、159. 如图,在的正方形方格中,每个小正方形方格的边长都为1,则和的关系是( ) A、 B、 C、 D、10. 如图等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( )
A、 B、 C、 D、10. 如图等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 在中, , , 则为 度12. 如图,在中, , 点D在AB边上,将沿CD折叠,使点B恰好落在AC边上的点E处,若 , 则的度数是
 13. 纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为 .
13. 纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为 .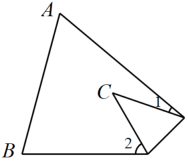 14. 如图,在中, , 分别以为边向上作正方形、正方形、正方形 , 点在上,若 , 则图中阴影的面积为 .
14. 如图,在中, , 分别以为边向上作正方形、正方形、正方形 , 点在上,若 , 则图中阴影的面积为 . 15. 如图,在中,的垂直平分线交于点D,连接 . 若 , , 则的周长是 .
15. 如图,在中,的垂直平分线交于点D,连接 . 若 , , 则的周长是 . 16. 如图,在 中, , 是 边上除 , 点外的任意一点,则 .
16. 如图,在 中, , 是 边上除 , 点外的任意一点,则 . 17. 如图1,是一款直播间的工作护眼灯.图2是它的示意图,已知灯臂AB=BC=52cm,夹角∠B=90°,折点B到桌面PQ的距离为48 cm,灯泡CD与桌面平行,则灯泡CD到桌面的高度为cm; 打开开关,因工作需要,保持AB不动,将∠B调到135°(如图3),则灯泡CD上升的高度为cm.
17. 如图1,是一款直播间的工作护眼灯.图2是它的示意图,已知灯臂AB=BC=52cm,夹角∠B=90°,折点B到桌面PQ的距离为48 cm,灯泡CD与桌面平行,则灯泡CD到桌面的高度为cm; 打开开关,因工作需要,保持AB不动,将∠B调到135°(如图3),则灯泡CD上升的高度为cm.
三、作图题
-
18. 如图,在中, .
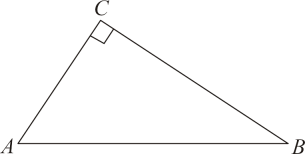 (1)、实践与操作:利用尺规作的外接圆,圆心为点O(要求:尺规作图并保留作图痕迹,不写作法,标明字母).(2)、猜想与证明:若 , 试猜想线段 与半径r的数量关系,并加以证明.
(1)、实践与操作:利用尺规作的外接圆,圆心为点O(要求:尺规作图并保留作图痕迹,不写作法,标明字母).(2)、猜想与证明:若 , 试猜想线段 与半径r的数量关系,并加以证明.四、解答题
-
19. 如图,在△ABD和△ACE中,有下列判断:

①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.
请用其中的三个判断作为条件,余下的一个判断作为结论(用序号⊗⊗⊗⇒⊗的形式),写出一个由三个条件能推出结论成立的式子,并说明理由.
20. 如图,在中,延长至点 , 连接 , 是上一点.已知 , , , 求的度数. 21. 如图,直线经过原点O,点A在x轴上,于点D,于点F,已知点 , , , , 求的长度.
21. 如图,直线经过原点O,点A在x轴上,于点D,于点F,已知点 , , , , 求的长度. 22. 根据以下素材,探索完成任务.
22. 根据以下素材,探索完成任务.三角形背景下角的关系探索
素材1
如图,已知等腰△ABC中,BA=BC,在腰BC的延长线上取点E,连结AE,作AE的中垂线交射线BC于点D,连结AD.

素材2
研究一个几何问题时,一般先根据几何语言画出几何图形.可能需要分类讨论.
素材3
当我们要论证一个一般性结论时,常常将问题先分成几种特例,在研究特例的过程中寻求规律,总结方法,猜测结论,再将规律、方法和结论迁移到一般情形中,这种数学推理方法叫做归纳法.
问题解决
任务1
补全图形
请根据素材1,把图形补全.你画的点D在点C的 ▲ 侧.
任务2
特例猜想
有下列条件:①AB=AC;②∠B=40°;③∠CEA=20°;④∠CEA=50°;请从中选择你认为合适的一个或两个条件作为已知条件,求出∠BAD和∠CAE的大小,并猜测∠BAD与∠CAE的数量关系.
任务3
一般结论
请根据你在任务1中所画的一般情况下的图形,写出∠BAD与∠CAE的数量关系,并说明理由.
任务4
拓展延伸
除了你在任务1中所画的情形外,点D相对于点C的位置还有不同的情形吗?若有,请画出图形,并直接写出∠BAD与∠CAE的数量关系.
23. 小明在学习过程中,对教材中的一个有趣问题做如下探究: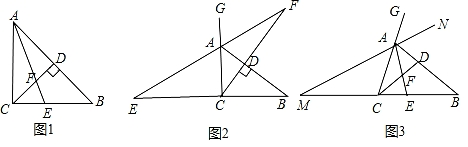
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
-