人教版备考2023中考数学二轮复习 专题16 图形认识初步与平行线
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 下列语句中,是真命题的是( )A、已知 , 求a的值 B、面积相等的两个三角形全等 C、对顶角相等 D、若 , 则2. 如图,把长方形沿对折后使两部分重合,若 , 则( )
 A、 B、 C、 D、3. 如图,在一全封闭的圆柱形玻璃容器中装一半的水,水平放置时,水面的形状是( )
A、 B、 C、 D、3. 如图,在一全封闭的圆柱形玻璃容器中装一半的水,水平放置时,水面的形状是( ) A、梯形 B、长方形 C、平行四边形 D、圆4. 如图,点O在直线上,射线是的平分线,若 , 则的度数是( )
A、梯形 B、长方形 C、平行四边形 D、圆4. 如图,点O在直线上,射线是的平分线,若 , 则的度数是( ) A、20° B、45° C、60° D、70°5. 如图,已知平分 , 是延长线上一点,则的度数是( )
A、20° B、45° C、60° D、70°5. 如图,已知平分 , 是延长线上一点,则的度数是( ) A、 B、 C、 D、6. 如图,在中, , , , 则射线 与 ( )
A、 B、 C、 D、6. 如图,在中, , , , 则射线 与 ( ) A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交7. 棋盘上有黑、白两色棋子若干,如果两颗棋子连成的直线上只有颜色相同的棋子,我们就称“同棋共线”.右图中“同棋共线”的直线共有( )
A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交7. 棋盘上有黑、白两色棋子若干,如果两颗棋子连成的直线上只有颜色相同的棋子,我们就称“同棋共线”.右图中“同棋共线”的直线共有( ) A、8条 B、10条 C、12条 D、16条8. 如图,在半径为的中,弦 , 是弦上一动点,则的最小值为( )
A、8条 B、10条 C、12条 D、16条8. 如图,在半径为的中,弦 , 是弦上一动点,则的最小值为( ) A、3 B、 C、2 D、19. 如图,和的平分线交于点 , 过点作分别交 , 于点 , , 若 , , 则线段的长为( )
A、3 B、 C、2 D、19. 如图,和的平分线交于点 , 过点作分别交 , 于点 , , 若 , , 则线段的长为( ) A、16 B、17 C、18 D、1910. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )
A、16 B、17 C、18 D、1910. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )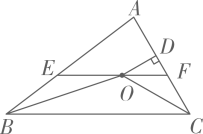 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,在中,平分交于点D,平分交于点E,若 , 则 .
 12. 如图,在锐角△ABC中,∠A=75°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为 °.
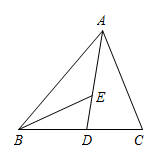
12. 如图,在锐角△ABC中,∠A=75°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为 °.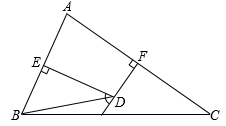 13. 如图,在Rt△ABC中,∠A=90°,∠B=30°,CD平分∠ACB交AB于点D,DE∥BC,交AC于点E,若BC=9,则AE的长为 .
13. 如图,在Rt△ABC中,∠A=90°,∠B=30°,CD平分∠ACB交AB于点D,DE∥BC,交AC于点E,若BC=9,则AE的长为 . 14. 在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是 .
14. 在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是 . 15. 七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”小林将图1的一副七巧板拼成图2的“衣服”阴影部分 , 并将它放入方格图中,方格图中的小正方形边长为1,则这件“衣服”的周长为取1.4).
15. 七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”小林将图1的一副七巧板拼成图2的“衣服”阴影部分 , 并将它放入方格图中,方格图中的小正方形边长为1,则这件“衣服”的周长为取1.4). 16. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF;则以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;其中正确的结论有 .
16. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF;则以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;其中正确的结论有 . 17. 图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚米,米,为上固定连接点,靠背米.档位为Ⅰ档时, , 档位为Ⅱ档时,当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端向后靠的水平距离即为米.
17. 图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚米,米,为上固定连接点,靠背米.档位为Ⅰ档时, , 档位为Ⅱ档时,当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端向后靠的水平距离即为米.
三、解答题
-
18. 如图,在ABC中,AD是ABC的高,AE、BF是ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
 19. 如图,C为∠AOB平分线上一点,点D在射线OA上,且OD=CD.
19. 如图,C为∠AOB平分线上一点,点D在射线OA上,且OD=CD.求证:CD∥OB.
 20. 如图,的平分线与的外角的平分线相交于点P.若 , 求的度数.
20. 如图,的平分线与的外角的平分线相交于点P.若 , 求的度数.
四、综合题
-
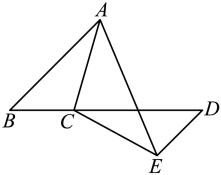
21. 如图

 (1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).
(1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).