人教版备考2023中考数学二轮复习专题13 二次函数

试卷更新日期：2023-01-05 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列函数中，是二次函数的是（）

A、y＝- $\frac{11}{x^{2}}$ B、y＝2x²-x+2 C、y＝ $\frac{1}{x}$ D、y＝2x+2

查看试题解析
2. 将抛物线y＝2x²向左平移3个单位，再向上平移5个单位，得到的抛物线的表达式为（）

A、y＝2（x-3）²-5 B、y＝2（x+3）²-5 C、y＝2（x-3）²+5 D、y＝2（x+3）²+5

查看试题解析
3. 已知 $(3 ， y_{1})$ ， $(5 ， y_{2})$ 是抛物线 $y = x^{2} - 2 x - 1$ 图象上两点，则 $y_{1}$ ， $y_{2}$ 的大小关系（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、无法确定

查看试题解析
4. 二次函数 $y = x^{2} - 2 x - 3$ ．若 $y > - 3$ ，则自变量x的取值范围是（）

A、 $x < 0$ 或 $x > 2$ B、 $x < 1$ 或 $x > 3$ C、 $0 < x < 2$ D、 $1 < x < 3$

查看试题解析
5. 由二次函数 $y = 2 {(x - 3)}^{2} + 1$ ，可知（ )

A、其图象的开口向下 B、其图象的对称轴为直线 $x = - 3$ C、其最小值为1 D、当x＜3时，y随x的增大而增大

查看试题解析
6. 王刚在练习投篮，篮球脱手后的运动轨迹近似为如图所示的抛物线 $y = - 0.2 x^{2} + x + 2.25$ ，已知篮圈高 $3.05$ 米，王刚投篮时出手高度 $O B$ 为 $2.25$ 米，若要使篮球刚好投进篮圈C，则投篮时王刚离篮圈中心的水平距离为（）

A、 $2$ 米 B、 $3$ 米 C、 $4$ 米 D、 $5$ 米

查看试题解析
7. 抛物线 $y = x^{2} - 2 x + 1$ 与坐标轴的交点个数为（）

A、无交点 B、1个 C、2个 D、3个

查看试题解析
8. 抛物线 $y = a x^{2} + b x + c$ （a，b，c是常数）， $a > 0$ ，顶点坐标为 $(1 ， m)$ ，给出下列结论：①若点 $(n ， y_{1})$ 与 $(3 - 2 n ， y_{2})$ 在该抛物线上，当 $n < 1$ 时，则 $y_{1} < y_{2}$ ；②关于x的一元二次方程 $a x^{2} + b x + c - m + 1 = 0$ 无实数解，那么（）.

A、①正确，②正确 B、①正确，②错误 C、①错误，②正确 D、①错误，②错误

查看试题解析
9. 如图是二次函数 $y = a x^{2} + b x + c$ 图象的一部分，图象过点 $A (- 3 ， 0)$ ，对称轴为直线 $x = - 1$ ， ① $b^{2} - 4 a c > 0$ ② $4 a + c < 0$ ③当 $- 3 \leq x \leq 1$ 时， $y \geq 0$ ④若 $B (- \frac{5}{2} ， y_{1})$ ， $C (- \frac{1}{2} ， y_{2})$ 为函数图象上的两点，则 $y_{1} > y_{2}$ ，以上结论中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

10. 已知二次函数 $y = - x^{2} + 2 x$ ，当 $- 1 < x < a$ 时，y随x的增大而增大，则实数a的取值范围是

查看试题解析
11. 如图所示，已知抛物线 $C_{1}$ ，抛物线 $C_{2}$ 关于原点中心对称．如果抛物线 $C_{1}$ 的解析式为 $y = \frac{3}{4} (x + 2)^{2} - 1$ ，那么抛物线 $C_{2}$ 的顶点坐标是，解析式为．

查看试题解析
12. 已知顶点为 $A$ 的抛物线 $y_{1} = x^{2} + b_{1} x + c$ 与顶点为 $C$ 的抛物线 $y_{2} = - x^{2} + b_{2} x + c_{2}$ 交于 $B (m ， n)$ ， $D (m + 6 ， n)$ ，则四边形 $A B C D$ 的周长为.

查看试题解析
13. 如图，在平面直角坐标系中，菱形 $A B C D$ 的顶点 $A$ 在 $x$ 轴负半轴上，顶点 $B$ 在 $x$ 轴正半轴上.若抛物线 $p = a x^{2} - 10 a x + 8 (a > 0)$ 经过点 $C$ 、 $D$ ，则点 $B$ 的坐标为.

查看试题解析
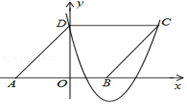14. 设二次函数y₁＝-mx²+nx-1，y₂＝-x²-nx-m（m，n是实数，m≠0）的最大值分别是p，q，若p+q＝0，则p＝， q＝.

查看试题解析
15. 在直角坐标系 $x O y$ 中，对于点 $P (x ， y)$ 和 $Q (x ， y^{'})$ ，给出如下定义：若 $y^{'} = {\begin{array}{l} y (x \geq 0) \\ - y (x < 0) \end{array}$ 称点Q为点P的“可控变点”，例如：点 $(1 ， 2)$ 的“可控变点”为点 $(1 ， 2)$ ，点 $(- 1 ， 3)$ 的“可控变点”为点 $(- 1 ， - 3)$ .

(1)、若点 $(- 1 ， - 2)$ 是一次函数 $y = x + 3$ 图象上点M的“可控变点”，则点M的坐标为；

(2)、若点P在函数 $y = - x^{2} + 18 (- 5 \leq x \leq a)$ 的图象上，其“可控变点”Q的纵坐标 $y^{'}$ 的取值范围是 $- 18 < y^{'} \leq 18$ ，则实数a的取值范围是.

查看试题解析

三、作图题

16. “水城河畔，樱花绽放，凉都宫中，书画成风”的风景，引来市民和游客争相“打卡”留念．已知水城河与南环路之间的某路段平行宽度为200米，为避免交通拥堵，请在水城河与南环路之间设计一条停车带，使得每个停车位到水城河与到凉都宫点 $F$ 的距离相等．

(1)、利用尺规作出凉都宫到水城河的距离（保留作图痕迹，不写作法）；

(2)、在图中格点处标出三个符合条件的停车位 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ；

(3)、建立平面直角坐标系，设 $M (0 ， 2)$ ， $N (2 ， 0)$ ，停车位 $P (x ， y)$ ，请写出 $y$ 与 $x$ 之间关系式，在图中画出停车带，并判断点 $P (4 ， - 4)$ 是否在停车带上．

查看试题解析

四、解答题

17. 已知二次函数 $y = 2 x^{2} - x + 1$ ，当-1≤x≤1时，求函数y的最小值和最大值．

当 $x = - 1$ 时，则 $y = 2 \times {(- 1)}^{2} - (- 1) + 1 = 4$ .

当 $x = 1$ 时，则 $y = 2 \times 1^{2} - 1 + 1 = 2$

所以函数 $y$ 的最小值为2，最大值为4

彤彤的解答正确吗？如果不正确，请写出正确的解答.

查看试题解析
18. 体育测试时，九年级一名学生，双手扔实心球．已知实心球所经过的路线是某个二次函数图象的一部分，如果球出手处 $A$ 点距离地面的高度为 $2 m$ ，当球运行的水平距离为 $4 m$ 时，达到最大高度 $4 m$ 的 $B$ 处（如图），问该学生把实心球扔出多远？（结果保留根号）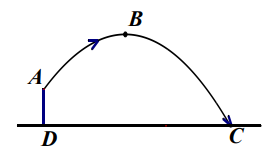

查看试题解析
19. 如图，在平面直角坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A(1，0)，B(0，2)，抛物线y= $\frac{1}{2}$ x²+bx-2过点C．求抛物线的表达式．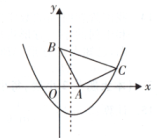

查看试题解析

五、综合题

20. 抛物线 $y ＝ x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ ，点 $B (2 ， - 3)$ ，与y轴交于点C，抛物线的顶点为D．

(1)、求抛物线的解析式；

(2)、当 $0 < x < 4$ 时，y的取值范围是；

(3)、抛物线上是否存在点P，使 $△ PBC$ 的面积是 $△ B C D$ 面积的4倍，若存在，点P的坐标；若不存在，请说明理由．

查看试题解析
21. 如图，直线y＝-x+m与抛物线y＝ax²+bx都经过点A（6，0），点B，过B作BH垂直x轴于H，OA＝3OH．直线OC与抛物线AB段交于点C．

(1)、求抛物线的解析式；

(2)、当点C的纵坐标是 $\frac{5}{2}$ 时，求直线OC与直线AB的交点D的坐标；

(3)、在（2）的条件下将△OBH沿BA方向平移到△MPN，顶点P始终在线段AB上，求△MPN与△OAC公共部分面积的最大值．

查看试题解析
22. 二次函数 $y = a x^{2} + b x + 4$ （a≠0）的图象经过点A（-4，0）、B（1，0），与y轴交于点C，点P为第二象限内抛物线上一点，连接BP、AC，交于点Q，过点P作PD⊥x轴于点D.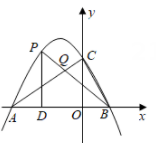

(1)、求二次函数的表达式；

(2)、连接BC，当∠DPB＝2∠BCO时，求直线BP的表达式；

(3)、请判断： $\frac{P Q}{Q B}$ 是否有最大值？如有请求出有最大值时点P的坐标，如没有请说明理由.

查看试题解析
23. 在平面直角坐标系中，点O为坐标的原点，抛物线 $y = a x^{2} + b x + 3$ 经过点 $B (- 3 ， 0)$ ，点 $C (1 ， 0)$ ，与y轴交于点A．

(1)、求a、b的值；

(2)、如图1，点P在抛物线上，过点P作 $P D ∥ y$ 轴交线段 $A B$ 于点D，设点P的横坐标为t，线段 $P D$ 的长为d，求d与t的函数解析式（不要求写出自变量t的取值范围）；

(3)、如图2，在（2）的条件下，连接 $C D$ ，过点A作 $A E ⊥ C D$ 于点F， $A E = C D$ ，过点E作 $E G ⊥ A B$ 于点G，过点G作 $G H ∥ D P$ 交x轴于点H，连接 $F H 、 F O$ ，若 $∠ H F O = 90 °$ ，求点P的坐标．

查看试题解析

人教版备考2023中考数学二轮复习 专题13 二次函数

一、单选题

二、填空题

三、作图题

四、解答题

五、综合题

人教版备考2023中考数学二轮复习专题13 二次函数