人教版备考2023中考数学二轮复习 专题12 一次函数
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 下列正比例函数中,y随x的增大而增大的是( )A、 B、 C、 D、2. 若y=(m-1)是正比例函数,则m的值为( )A、1 B、-1 C、1或-1 D、或-3. 对于函数y=-x+3,下列结论正确的是( )A、它的图象与两坐标轴围成等腰直角三角形 B、它的图象经过第一、二、三象限 C、它的图象必经过点(-1,3) D、y的值随x值的增大而增大4. 已知一次函数中,自变量与函数值的几组对应值如下表,根据表中数据判断,下列说法正确的是( )
x
……
-2
-1
1
2
3
……
y
……
-8
-1
13
20
27
……
A、该函数的表达式为 B、点不在该函数的图象上 C、该函数图象经过第一、二、三象限 D、该函数图象与坐标轴围成的三角形面积为75. 已知一次函数 , y随着x的增大而减小,则在直角坐标系内它的大致图象是( )A、 B、
B、 C、
C、 D、
D、 6. 已知正比例函数的图像上一点 , 且 , 则m的值可能是( )A、-0.5 B、0 C、1 D、1.57. 弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由此图可知不挂物体时弹簧的长度为( )
6. 已知正比例函数的图像上一点 , 且 , 则m的值可能是( )A、-0.5 B、0 C、1 D、1.57. 弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由此图可知不挂物体时弹簧的长度为( )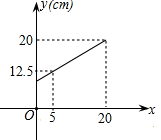 A、7cm B、8cm C、9cm D、10cm8. 如图,直线 与 交于点 , 有四个结论:① ;② ;③当 时,;④当 时, , 其中正确的是 ( )
A、7cm B、8cm C、9cm D、10cm8. 如图,直线 与 交于点 , 有四个结论:① ;② ;③当 时,;④当 时, , 其中正确的是 ( ) A、①② B、①③ C、①④ D、②④9. 在下列函数图象上任取不同的两点P(x1 , y1), Q(x2 , y2), 一定能使的是( )A、y=(x>0) B、y=-(x-2)2+5(x≥0) C、y=(x-3)2-4(x<0) D、y=3x+7
A、①② B、①③ C、①④ D、②④9. 在下列函数图象上任取不同的两点P(x1 , y1), Q(x2 , y2), 一定能使的是( )A、y=(x>0) B、y=-(x-2)2+5(x≥0) C、y=(x-3)2-4(x<0) D、y=3x+7二、填空题
-
10. 在一次函数 中,的值随着 值得增大而增大,请你写出一个符合条件的一次函数解析式 .11. 已知一次函数 , 若函数满足 , 则自变量的取值范围是 .12. 如图,在平面直角坐标系中,直线与直线相交于点 , 若点的横坐标为1,则关于的二元一次方程组的解是。
 13. 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式ax-3<3x+b≤0的解集是.
13. 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式ax-3<3x+b≤0的解集是. 14. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线y=x上,OA1B1 , B1A1A2 , B2B1A2 , B2A2A3 , B3B2A3…都是等腰直角三角形,且OA1=1,则点B2022的坐标是 .
14. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线y=x上,OA1B1 , B1A1A2 , B2B1A2 , B2A2A3 , B3B2A3…都是等腰直角三角形,且OA1=1,则点B2022的坐标是 .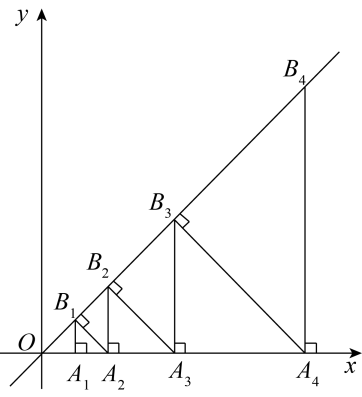
三、解答题
-
15. 如图,将直线向上平移2个单位,得到一个一次函数的图象,求这个一次函数的表达式.
 16. 已知 , 与成正比例,与x成反比例,并且当时,;当时, . 求y与x之间的函数关系式.17. 陕西某旅游景点的门票收费标准是:每人30元.某公司计划组织员工去该景点旅游,写出总门票费y(元)与人数x(人)之间关系式,并判断y是x的正比例函数吗?18. 如图
16. 已知 , 与成正比例,与x成反比例,并且当时,;当时, . 求y与x之间的函数关系式.17. 陕西某旅游景点的门票收费标准是:每人30元.某公司计划组织员工去该景点旅游,写出总门票费y(元)与人数x(人)之间关系式,并判断y是x的正比例函数吗?18. 如图
问题提出:
如图,等腰中, , , 直线经过点C,过点A作于点D,过点B作于点E,求证: ;
问题探究:
如图2,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角 , , 求点C的坐标;
问题解决:
古城西安已经全面迎来地铁时代!继西安地铁2号线于2011年9月16日通车试运行以来,共有八条线路开通运营,极大促进了西安市的交通运输,目前还有多条线路正在修建中.如图,地铁某线路原计划按OA-AB的方向施工,由于在AB方向发现一处地下古建筑,地铁修建须绕开此区域.经实地勘测,若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向,则可以绕开此区域.已知OA长为1千米,以点O为原点,OA所在直线为x轴,1千米为单位长度,建立平面直角坐标系,且射线AB与直线平行,请帮助施工队计算出AC和AD所在直线的解析式.
四、综合题
-
19. 如图,已知直线与轴交于点 , 将直线沿轴向上平移7个单位得到直线分别交轴、轴于点 , 且点的坐标为 , 点为线段BC上一点,连接OP.
 (1)、求点和点的坐标;(2)、是否存在点 , 使得OP将的面积分为1:2的两部分?若存在,求出A,P两点所在直线的函数表达式;若不存在,请说明理由.20. 已知:如图 , 在平面直角坐标系中,一次函数 交 轴于点 , 交 轴于点 , 点 是点 关于 轴对称的点,过点 作 轴平行的射线 , 交直线 与点 , 点 是射线 上的一个动点.
(1)、求点和点的坐标;(2)、是否存在点 , 使得OP将的面积分为1:2的两部分?若存在,求出A,P两点所在直线的函数表达式;若不存在,请说明理由.20. 已知:如图 , 在平面直角坐标系中,一次函数 交 轴于点 , 交 轴于点 , 点 是点 关于 轴对称的点,过点 作 轴平行的射线 , 交直线 与点 , 点 是射线 上的一个动点.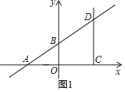
 (1)、求点 , 的坐标.(2)、如图 2,将 沿着 翻折,当点 的对应点 落在直线 上时,求点 的坐标.(3)、若直线 与直线 有交点,不妨设交点为 (不与点 重合),连接 , 是否存在点 , 使得 , 若存在,请求出对应的点 坐标;若不存在,请说明理由.
(1)、求点 , 的坐标.(2)、如图 2,将 沿着 翻折,当点 的对应点 落在直线 上时,求点 的坐标.(3)、若直线 与直线 有交点,不妨设交点为 (不与点 重合),连接 , 是否存在点 , 使得 , 若存在,请求出对应的点 坐标;若不存在,请说明理由.