人教版备考2023中考数学二轮复习 专题10 平面直角坐标系
试卷更新日期:2023-01-05 类型:二轮复习
一、单选题
-
1. 在平面直角坐标系中,下列坐标所对应的点位于第三象限的是( )A、(-1,2) B、(1,2) C、(2,-1) D、(-1,-3)2. 若点P(a,b)在第四象限,则点Q(-a,b-1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在如图所示的平面直角坐标系中,点P的坐标为( )
 A、 B、 C、 D、4. 如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )
A、 B、 C、 D、4. 如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )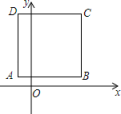 A、(3,1) B、(-1,1) C、(3,5) D、(-1,5)5. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )
A、(3,1) B、(-1,1) C、(3,5) D、(-1,5)5. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )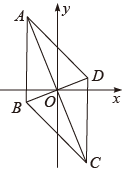 A、 B、 C、 D、6. 如图,在正方形网格中,线段绕点旋转一定的角度后与线段重合、均为格点,的对应点是点 , 若点的坐标为 , 点的坐标为 , 则旋转中心点的坐标为( )
A、 B、 C、 D、6. 如图,在正方形网格中,线段绕点旋转一定的角度后与线段重合、均为格点,的对应点是点 , 若点的坐标为 , 点的坐标为 , 则旋转中心点的坐标为( ) A、 B、 C、 D、或7. 如图,在平面直角坐标系中,点A的坐标是 , 点B的坐标是 , 点C是OB上一点,将沿AC折叠,点B恰好落在x轴上的点处,则点C的坐标为( )
A、 B、 C、 D、或7. 如图,在平面直角坐标系中,点A的坐标是 , 点B的坐标是 , 点C是OB上一点,将沿AC折叠,点B恰好落在x轴上的点处,则点C的坐标为( ) A、 B、 C、 D、8. 已知点的坐标为 , 下列说法正确的是( )A、若点在轴上, 则 B、若点在一三象限角平分线上, 则 C、若点到轴的距离是3 , 则 D、若点在第四象限, 则的值可以为-29. 我们规定:在平面直角坐标系中,任意不重合的两点 , 之间的折线距离为 , 例如图①中,点与点之间的折线距离为 . 如图②,已知点若点的坐标为 , 且 , 则的值为( )
A、 B、 C、 D、8. 已知点的坐标为 , 下列说法正确的是( )A、若点在轴上, 则 B、若点在一三象限角平分线上, 则 C、若点到轴的距离是3 , 则 D、若点在第四象限, 则的值可以为-29. 我们规定:在平面直角坐标系中,任意不重合的两点 , 之间的折线距离为 , 例如图①中,点与点之间的折线距离为 . 如图②,已知点若点的坐标为 , 且 , 则的值为( ) A、 B、 C、或 D、或10. 在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An , …若点A1的坐标为(2,4),点A2021的坐标为( )A、(3,﹣1) B、(﹣2,﹣2) C、(﹣3,3) D、(2,4 )
A、 B、 C、或 D、或10. 在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An , …若点A1的坐标为(2,4),点A2021的坐标为( )A、(3,﹣1) B、(﹣2,﹣2) C、(﹣3,3) D、(2,4 )二、填空题
-
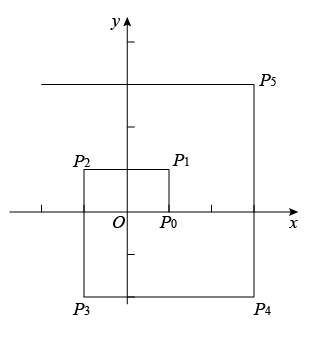
11. 在平面直角坐标系中,点(1,-2)向左平移2个单位后的坐标为。12. 已知点 , 点 , 若点M是线段AB的中点,则点M的坐标为 .13. 若点到轴的距离为4,则n= .14. 在平面直角坐标系中,把点P(1,-2)绕原点O顺时针旋转90°,所得到的对应点Q的坐标为 .15. 九年级某班有48名学生,所在教室有6行8列座位,用(m,n)表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为(m,n),若调整后的座位为(i,j),则称该生作了平移[a,b]=[m-i,n-j],并称a+b为该生的位置数.若某生的位置数为9,则当m+n取最小值时,m•n的最大值为.16. 如图:在直角坐标系中,设一动点自处向上运动1个单位至 , 然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,如此继续运动下去.设 , , 2,3…,则 .
三、作图题
-
17. 为了更好的开展古树名木的系统保护工作,某公园对园内的6棵百年古树都利用坐标确定了位置,并且定期巡视.

⑴在如图所示的正方形网格中建立平面直角坐标系 , 使得古树A,B的位置分别表示为 , ;
⑵在(1)建立的平面直角坐标系中,
①表示古树C的位置的坐标为 ▲ ;
②标出古树 , , 的位置.
四、解答题
-
18. 在平面直角坐标系中,已知点 , 点P在过点,且与x轴平行的直线上,求出点P的坐标.19. 已知点P坐标为(m﹣1,﹣m+2),那么点P能否是第三象限内的点?请说明理由.20. 如图,的顶点都在平面直角坐标系中的坐标轴上,的面积 , , , 求三个顶点的坐标.

五、综合题
-
21. 如图1,在平面直角坐标系中,点A的坐标为(8,0),点B的坐标是(0,6),连结AB.若动点P从点B出发沿着线段BA以5个单位每秒的速度向终点A运动,设运动时间为t秒.
 (1)、求线段AB的长.(2)、连接OP,当△OBP为等腰三角形时,过点P作线段AB的垂线与直线OB交于点M,求点M的坐标;(3)、已知N点为AB的中点,连结ON,点P关于直线ON的对称点记为P'(如图2),在整个运动过程中,若P'点恰好落在△AOB内部(不含边界),请直接写出t的取值范围.
(1)、求线段AB的长.(2)、连接OP,当△OBP为等腰三角形时,过点P作线段AB的垂线与直线OB交于点M,求点M的坐标;(3)、已知N点为AB的中点,连结ON,点P关于直线ON的对称点记为P'(如图2),在整个运动过程中,若P'点恰好落在△AOB内部(不含边界),请直接写出t的取值范围.
-