山西省吕梁市交城县2022-2023学年九年级上学期期末数学试卷

试卷更新日期：2023-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 方程x²﹣2x+3=0的根的情况是（　　）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有一个实数根

查看试题解析
2. 将一个长方体沿四条棱切割掉一个三棱柱后，得到如图所示的几何体，则该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点（3，-5），则该反比例函数的图象位于（）

A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限

查看试题解析
4.
如图是一个照相机成像的示意图，如果底片AB宽40mm，焦距是60mm，所拍摄的2m外的景物的宽CD为（　　）

A、12m B、3m C、 $\frac{3}{2}$ m D、 $\frac{4}{3}$ m

查看试题解析
5. 在下列四幅图形中，能表示两棵小树在同一时刻阳光下影子的图形的可能是（　　）

A、 B、 C、 D、

查看试题解析
6. 小明为估计一个不规则图案的面积，采取了以下办法：首先用一个面积为10cm²的长方形将不规则图案围起来（如图①）；然后在一固定位置随机朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在边界线上或长方形区域外不计试验结果）；最后将若干次有效试验的结果绘制成了图②所示的折线统计图．请估计不规则图案的面积大约为（）

A、4cm² B、3.5 cm² C、4.5 cm² D、5 cm²

查看试题解析
7. 如图，在菱形ABCD中，AC交BD于O， $D H ⊥ A B$ 于H，连接OH， $A C = 16$ ， $A B = 10$ ，则 $O H =$ （）．

A、2.4 B、4.8 C、9.6 D、6

查看试题解析
8. 若点 $A (- 1 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (3 ， y_{3})$ 在反比例函数 $y = - \frac{9}{x}$ 的图像上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
9. 按照党中央、国务院决策部署，为了活跃市场主体、助推各地区经济发展，各省市地区抓紧推动稳经济一揽子政策落实落地．江夏区制定了“黄金十条”，坚定企业疫后发展信心，促进企业稳步高效增长.2022年我区某企业4月份的利润是100万元，第二季度的总利润达到500万元，设利润平均月增长率为x，则依题意列方程为（）

A、 $100 (1 + x)^{2} = 500$ B、 $100 (1 + x^{2}) = 500$ C、 $100 (1 + x) + 100 (1 + x)^{2} = 500$ D、 $100 + 100 (1 + x) + 100 (1 + x)^{2} = 500$

查看试题解析
10. 如图，在正方形ABCD中，E为AD的中点，DF⊥CE于M，交AC于点N，交AB于点F，连接EN、BM、有如下结论：①△ADF≌△DCE；②MN=FN；③CN=2AN；④ $S_{△ A N D}$ ∶ $S_{四边形 C N F B}$ =2∶5；⑤∠ADF=∠BMF．其中正确结论的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 添加一个条件，使矩形ABCD是正方形，这个条件可能是．

查看试题解析
12. 如图， $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 位似，位似中心为点O， $O A = 2 A A^{^{'}}$ ， $△ A B C$ 的面积为4，则 $△ A^{'} B^{'} C^{'}$ 的面积为.

查看试题解析
13. 如下图，一个小球从A点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达G点的概率是．

查看试题解析
14. 如图，点A在双曲线 $y = \frac{4}{x}$ 上，点B在双曲线 $y = \frac{k}{x}$ （k≠0）上，AB∥x轴，分别过点A，B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是8，则k的值为．

查看试题解析
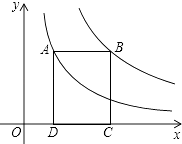15. 如图，在矩形ABCD中，AB＝6，AD＝8，E、F分别为AB、CD边上的点，且EF∥BC，G为EF上一点，且GF＝2，M、N分别为GD、EC的中点，则MN＝.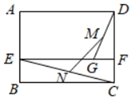

查看试题解析

三、解答题

16. 解方程：

(1)、x（x-4）+1＝0；

(2)、（2x-3）²＝5（2x-3）．

查看试题解析
17. 如图是两根木杆及其影子的图形.

(1)、这个图形反映的是中心投影还是平行投影?答：

(2)、请你在图中画出表示小树影长的线段AB.

查看试题解析
18. 为迎接中国共产党成立100周年，让更多人了解红色文化艺术，凝聚和弘扬红色文化，某市举办一百周年红色文旅美术展活动，小唯与小亮都想去观展，但只有一张门票，于是两人想通过摸卡片的方式来决定谁去观展，规则如下：现有两组卡片，第一组卡片上写有A，B，C，第二组卡片上写有A，B，B，C，这两组卡片上除字母外其余均相同．将卡片正面朝下洗匀，随机抽取一张，记下字母后放回，称为摸卡片一次．

(1)、若小亮从第二组中摸卡片12次，其中8次摸出的卡片上写有字母B，求这12次摸出的卡片上写有字母B的频率；

(2)、小唯从第一组中摸卡片一次，小亮从第二组中摸卡片一次，若摸出的卡片上所写字母均为字母B，则小唯去观展，请用列表或画树状图的方法，求小唯去观展的概率．

查看试题解析
19. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且DE＝ $\frac{1}{2}$ AC，连接CE、OE，OE交DC于点F．

(1)、求证：四边形OCED是矩形；

(2)、若AD＝6，求OF的长．

查看试题解析
20. 5月10日上午，庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行，习近平总书记重要讲话引发各界青年热烈反响．某校为庆祝共青团成立100周年升起了共青团旗帜，李优和贺基旭想用所学知识测量该旗帜的宽度MN，他们进行了如下操作：如图，首先，李优在C处竖立一根标杆 $B C$ ，地面上的点A、标杆顶端B和点N在一条直线上， $B C = 1.5$ 米， $A C = 1$ 米， $A G = 8$ 米；然后，贺基旭手持自制直角三角纸板 $D E F$ ，使长直角边 $D F$ 与水平地面平行，调整位置，恰好在P点时点D、E、M在一条直线上， $D P = 1.5$ 米， $P G = 23.6$ 米， $D F = 2 E F$ ，已知 $D P ⊥ P A$ ， $M G ⊥ P A$ ， $B C ⊥ P A$ ，点P、G、C、A在同一水平直线上，点N在 $M G$ 上，求旗帜的宽度 $M N$ ．

查看试题解析
21. 为防控新冠疫情，减少交叉感染，某超市在线上销售优质农产品．若农产品每盒进价25元，原售价为每盒40元．超市四月份的销售量达到400盒，该超市五月份降价促销．经调查发现，若该农产品每盒降价1元，月销售量可增加5盒，设农产品每盒降价x元，请解答下列问题．

(1)、用含x的代数式表示：则每盒获利元，五月份可售出盒；

(2)、这种农产品在五月份可获利4250元，求农产品每盒降价x的值．

查看试题解析
22. 背景：一次小组合作探究课上，小明将两个正方形按背景图位置摆放（点E，A，D在同一条直线上），发现BE=DG且BE⊥DG．小组讨论后，提出了三个问题，请你帮助解答：

(1)、将正方形AEFG绕点A按逆时针方向旋转，（如图1）还能得到BE=DG吗？如果能，请给出证明．如若不能，请说明理由：

(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD，将菱形AEFG绕点A按顺时针方向旋转，（如图2）试问当∠EAG与∠BAD的大小满足怎样的关系时，背景中的结论BE=DG仍成立？请说明理由；

(3)、把背景中的正方形改成矩形AEFG和矩形ABCD，且 $\frac{A E}{A G} = \frac{A B}{A D} = \frac{2}{3}$ ，AE=4，AB=8，将矩形AEFG绕点A按顺时针方向旋转（如图3），连接DE，BG．小组发现：在旋转过程中， BG²+DE²是定值，请求出这个定值．

查看试题解析
23. 如图，在平面直角坐标系中，A（8，0）、B（0，6）是矩形OACB的两个顶点，双曲线y＝ $\frac{k}{x}$ （k≠0，x＞0）经过AC的中点D，点E是矩形OACB与双曲线y＝ $\frac{k}{x}$ 的另一个交点．

(1)、点D的坐标为，点E的坐标为；

(2)、动点P在第一象限内，且满足S△PBO＝ $\frac{5}{6}$ S△ODE．
①若点P在这个反比例函数的图象上，求点P的坐标；
②若点Q是平面内一点，使得以A、C、P、Q为顶点的四边形是菱形，请你直接写出满足条件的所有点Q的坐标．

查看试题解析