山东省烟台市莱州市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 如图所示的几何体的俯视图是( )
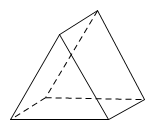 A、
A、 B、
B、 C、
C、 D、
D、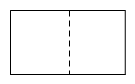 2. 下列关系式中,哪个等式表示y是x的反比例函数( )A、 B、 C、 D、3. 2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习,如图,一位同学乘滑雪板沿斜坡笔直滑下100米,若斜坡的坡比为 , 用计算器求下滑的水平距离,则下列按键顺序正确的是( )
2. 下列关系式中,哪个等式表示y是x的反比例函数( )A、 B、 C、 D、3. 2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习,如图,一位同学乘滑雪板沿斜坡笔直滑下100米,若斜坡的坡比为 , 用计算器求下滑的水平距离,则下列按键顺序正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 若 , , 则以点O为圆心,为半径的圆与直线的位置关系是( )A、相交 B、相切 C、相离 D、不能确定5. 如图,在⊙O中, , 若 , 则的度数是( )
4. 若 , , 则以点O为圆心,为半径的圆与直线的位置关系是( )A、相交 B、相切 C、相离 D、不能确定5. 如图,在⊙O中, , 若 , 则的度数是( ) A、 B、 C、 D、6. 如图,△ABC是⊙O的内接三角形,半径OB=3,sinA= ,则弦BC的长为( )
A、 B、 C、 D、6. 如图,△ABC是⊙O的内接三角形,半径OB=3,sinA= ,则弦BC的长为( )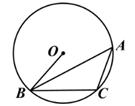 A、3 B、4 C、5 D、3.757. 如图,点B在y轴的正半轴上,点C在反比例函数的图象上,菱形的面积为8,则k的值为( )
A、3 B、4 C、5 D、3.757. 如图,点B在y轴的正半轴上,点C在反比例函数的图象上,菱形的面积为8,则k的值为( ) A、-4 B、4 C、-2 D、28. 已知,一轮船以16海里时的速度从港口A出发向北偏东方向航行,另一轮船以8海里时的速度同时从港口A出发向南偏东方向航行,则离开港口1小时后,两船相距( )A、海里 B、海里 C、16海里 D、24海里9. 如图是二次函数的图象,则函数的图象可能是( )
A、-4 B、4 C、-2 D、28. 已知,一轮船以16海里时的速度从港口A出发向北偏东方向航行,另一轮船以8海里时的速度同时从港口A出发向南偏东方向航行,则离开港口1小时后,两船相距( )A、海里 B、海里 C、16海里 D、24海里9. 如图是二次函数的图象,则函数的图象可能是( )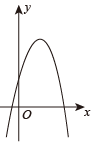 A、
A、 B、
B、 C、
C、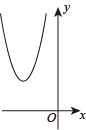 D、
D、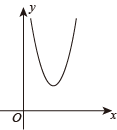 10. 如图,抛物线交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
10. 如图,抛物线交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.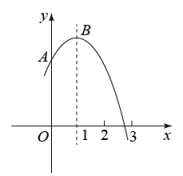
①一元二次方程有两个相等的实数根;②若点 , , 在该函数图象上,则;③将该抛物线先向左平移1个单位,再沿x轴翻折,得到的抛物线表达式是;④在y轴上找一点D,使的面积为1,则D点的坐标为.以上四个结论中正确的个数是( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若函数是二次函数,则m的值为 .12. 点、在反比例函数的图象上,若 , 则k的取值范围是 .13. 把一条长2m的铁丝折成顶角为的等腰三角形,那么这个三角形外接圆的半径为m.14. 已知直线m与半径为5cm的⊙O相切于点P,AB是⊙O的一条弦,且 , 若AB=6cm,则直线m与弦AB之间的距离为 .15. 如图,若被击打的小球飞行高度 (单位: )与飞行时间 (单位: )直接具有的关系为 ,则小球从飞出到落地所用的时间为s.
 16. 如图,平面直角坐标系中,的半径为 , 交x轴正半轴于点B,弦 , 点P为y轴上一点,且的值最小,则点P坐标为 .
16. 如图,平面直角坐标系中,的半径为 , 交x轴正半轴于点B,弦 , 点P为y轴上一点,且的值最小,则点P坐标为 .
三、解答题
-
17. 计算: -sin60°(1-sin30°).18. 如图,一拱形桥呈抛物线状,桥的最大高度为 , 跨度为 , 则离中心M点处的地方,桥的高度是多少?
 19. 如图,为等腰直角三角形,斜边在x轴上,一次函数的图象经过点A,交y轴于点C,反比例函数的图像也经过点A.
19. 如图,为等腰直角三角形,斜边在x轴上,一次函数的图象经过点A,交y轴于点C,反比例函数的图像也经过点A.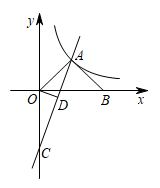 (1)、求反比例函数的解析式;(2)、过O点作于点,求的值.20. 如图,是的直径,点P是上一点,且点P是弦的中点.
(1)、求反比例函数的解析式;(2)、过O点作于点,求的值.20. 如图,是的直径,点P是上一点,且点P是弦的中点. (1)、依题意画出弦;(尺规作图不写作法,保留作图痕迹)(2)、若 , , 求的半径.21. 某种商品上市之初采用了大量的广告宣传,其日销售量y与上市的天数x之间成正比例函数,当广告停止后,日销售量y与上市的天数x之间成反比例函数(如图所示),现已知上市20天时,当日销售量为100件.
(1)、依题意画出弦;(尺规作图不写作法,保留作图痕迹)(2)、若 , , 求的半径.21. 某种商品上市之初采用了大量的广告宣传,其日销售量y与上市的天数x之间成正比例函数,当广告停止后,日销售量y与上市的天数x之间成反比例函数(如图所示),现已知上市20天时,当日销售量为100件. (1)、写出该商品上市以后日销售量y件与上市的天数x天之间的表达式;(2)、广告合同约定,当日销售量不低于80件,并且持续天数不少于10天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”,并说明理由?22. 如图1是小明在健身器材上进行仰卧起坐锻炼时的情景,图2是小明锻炼时上半身由位置运动到与底面CD垂直的位置时的示意图,已知米,米,(参考数据:)
(1)、写出该商品上市以后日销售量y件与上市的天数x天之间的表达式;(2)、广告合同约定,当日销售量不低于80件,并且持续天数不少于10天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”,并说明理由?22. 如图1是小明在健身器材上进行仰卧起坐锻炼时的情景,图2是小明锻炼时上半身由位置运动到与底面CD垂直的位置时的示意图,已知米,米,(参考数据:)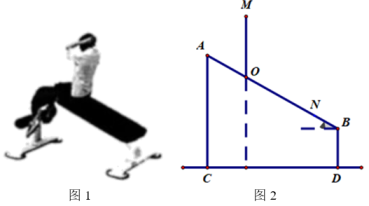 (1)、求的长(2)、若米,求两点的距离(精确0.01)23. 如图,是的直径,射线交于点D,E是劣弧上一点,且平分 , 过点E作于点F,延长 , 交延长线于点G.
(1)、求的长(2)、若米,求两点的距离(精确0.01)23. 如图,是的直径,射线交于点D,E是劣弧上一点,且平分 , 过点E作于点F,延长 , 交延长线于点G. (1)、求证:是的切线;(2)、若 , , 求的长.24. 霞峰桃是钢城特色农产品之一,为铺开销售渠道,当地政府引导果农进行网络销售.在试销售期间发现,该种桃的月销售量y(单位:千克)与销售单价x(单位:元)成一次函数关系,函数图象如图所示,已知该种桃的销售成本为5元/千克.
(1)、求证:是的切线;(2)、若 , , 求的长.24. 霞峰桃是钢城特色农产品之一,为铺开销售渠道,当地政府引导果农进行网络销售.在试销售期间发现,该种桃的月销售量y(单位:千克)与销售单价x(单位:元)成一次函数关系,函数图象如图所示,已知该种桃的销售成本为5元/千克. (1)、求y关于x的函数解析式(不需要写出自变量的取值范围);(2)、求销售该种桃每月可获得的最大利润;(3)、在销售过程中发现,该种桃每千克还需要支付1元的保鲜成本,若月销售量y与销售单价x保持(1)中的函数关系不变,当该种桃的月销售利润是105000元时,在最大限度减少库存的条件下,求x的值.25. 如图,抛物线与x轴负半轴交于点A(-1,0),与x轴的另一交点为B,与y轴正半轴交于点C(0,3),抛物线的对称轴与直线BC相交于点M,与x轴交于点G.
(1)、求y关于x的函数解析式(不需要写出自变量的取值范围);(2)、求销售该种桃每月可获得的最大利润;(3)、在销售过程中发现,该种桃每千克还需要支付1元的保鲜成本,若月销售量y与销售单价x保持(1)中的函数关系不变,当该种桃的月销售利润是105000元时,在最大限度减少库存的条件下,求x的值.25. 如图,抛物线与x轴负半轴交于点A(-1,0),与x轴的另一交点为B,与y轴正半轴交于点C(0,3),抛物线的对称轴与直线BC相交于点M,与x轴交于点G.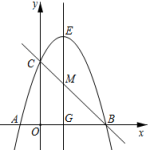 (1)、求抛物线的解析式及对称轴;(2)、抛物线的对称轴上存在点P,且点P在x轴上方时,满足∠APB=∠ABC,求PG的长.
(1)、求抛物线的解析式及对称轴;(2)、抛物线的对称轴上存在点P,且点P在x轴上方时,满足∠APB=∠ABC,求PG的长.