山东省青岛市胶州市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 如图所示几何体的左视图是( )
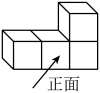 A、
A、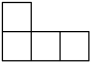 B、
B、 C、
C、 D、
D、 2. 如图,斜坡长 , 坡顶离地面的高度为 , 则此斜坡的倾斜角为( )
2. 如图,斜坡长 , 坡顶离地面的高度为 , 则此斜坡的倾斜角为( ) A、 B、 C、 D、3. 如图,在一间黑屋子的地面A处有一盏探照灯,当人从灯向墙运动时,他在墙上的影子的大小变化情况是( )
A、 B、 C、 D、3. 如图,在一间黑屋子的地面A处有一盏探照灯,当人从灯向墙运动时,他在墙上的影子的大小变化情况是( ) A、变大 B、变小 C、不变 D、不能确定4. 已知反比例函数的图象具有下列特征:在所在象限内,y 的值随 x 的增大而减小,那么m的取值范围是( )A、 B、 C、 D、5. 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
A、变大 B、变小 C、不变 D、不能确定4. 已知反比例函数的图象具有下列特征:在所在象限内,y 的值随 x 的增大而减小,那么m的取值范围是( )A、 B、 C、 D、5. 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( ) A、1 B、 C、 D、6. 点均在二次函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2021年底某市汽车拥有量为万辆,已知2019年底该市汽车拥有量为10万辆,如果设 2019 年底至2021年底该市汽车拥有量的年均增长率为x,那么根据题意列出的方程为( )A、 B、 C、 D、8. 二次函数的图象如图所示,则反比例函数与一次函数在同一坐标系内的图象大致是( )
A、1 B、 C、 D、6. 点均在二次函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2021年底某市汽车拥有量为万辆,已知2019年底该市汽车拥有量为10万辆,如果设 2019 年底至2021年底该市汽车拥有量的年均增长率为x,那么根据题意列出的方程为( )A、 B、 C、 D、8. 二次函数的图象如图所示,则反比例函数与一次函数在同一坐标系内的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 计算:2sin30°- cos 45°= .10. 若 , 那么的值为 .11. 如图,在 中, , 过 上一点 D 作直线交于点 F,使所得的三角形与原三角形相似,这样的直线可以作出的条数为 .
 12. 请写出一个满足条件①②的二次函数表达式 .
12. 请写出一个满足条件①②的二次函数表达式 .①图象的对称轴为直线;②图象经过点
13. 如图是某几何体的三视图,其俯视图为等边三角形,则该几何体的左视图的面积为 14. 如图,在正方形中,E为的中点,F为的中点, 的延长线与的延长线交于点H,与相交于点G,若 , 则的长为 .
14. 如图,在正方形中,E为的中点,F为的中点, 的延长线与的延长线交于点H,与相交于点G,若 , 则的长为 .
三、解答题
-
15. 已知: , , 求作:矩形 .
 16.(1)、解方程:;(2)、用配方法确定二次函数图象的对称轴和顶点坐标.17. 为弘扬祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小颖同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“柳暗花明又一村”.
16.(1)、解方程:;(2)、用配方法确定二次函数图象的对称轴和顶点坐标.17. 为弘扬祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小颖同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“柳暗花明又一村”. (1)、小明回答该问题时,仅对第二个字是选“暗”还是选“岸”难以抉择,若随机选择其中一个,则小明回答正确的概率是;(2)、小颖回答该问题时,对第二个字是选“暗”还是选“岸”、第四个字是选“名”还是选“明”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小颖回答正确的概率.18. 如图是旗杆竖直放置在矩形平台EFMC上的示意图,在某一时刻旗杆AB形成的影子的顶端恰好落在斜坡的D处,点F,M,D在一条直线上,现测得 , , , 求旗杆的高度.
(1)、小明回答该问题时,仅对第二个字是选“暗”还是选“岸”难以抉择,若随机选择其中一个,则小明回答正确的概率是;(2)、小颖回答该问题时,对第二个字是选“暗”还是选“岸”、第四个字是选“名”还是选“明”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小颖回答正确的概率.18. 如图是旗杆竖直放置在矩形平台EFMC上的示意图,在某一时刻旗杆AB形成的影子的顶端恰好落在斜坡的D处,点F,M,D在一条直线上,现测得 , , , 求旗杆的高度. 19. 《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等,现在我们来研究另一种特珠的自然数——“纯数”.
19. 《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等,现在我们来研究另一种特珠的自然数——“纯数”.定义:对于自然数n,在计算时,各数位都不产生进位,则称这个自然数n为“纯数”.
例如:32是“纯数”,因为计算时,各数位都不产生进位;23不是“纯数”,因为计算时,个位产生了进位.
(1)、判断2022是否是“纯数”?请说明理由;(2)、请直接写出2023到2050之间的“纯数”;不大于100的“纯数”的个数为 .20. 如图,在矩形中, , 在边 上是否存在一点 E,使?若存在,求出的长;若不存在,请说明理由. 21. 如图,已知一次函数的图象与x轴,y轴分别交于点A,B,且与反比例函数的图象在第二象限内的部分交于点C,垂直于x轴,垂足为D,其中 .
21. 如图,已知一次函数的图象与x轴,y轴分别交于点A,B,且与反比例函数的图象在第二象限内的部分交于点C,垂直于x轴,垂足为D,其中 . (1)、直接写出A,B两点的坐标;(2)、求这两个函数的关系式;(3)、若点P在x轴上,且 , 请直接写出点P的坐标.22. 如图在平行四边形中,O 为对角线 的中点,过点 O 的直线 分别交 , 于点 E,F.
(1)、直接写出A,B两点的坐标;(2)、求这两个函数的关系式;(3)、若点P在x轴上,且 , 请直接写出点P的坐标.22. 如图在平行四边形中,O 为对角线 的中点,过点 O 的直线 分别交 , 于点 E,F. (1)、求证:;(2)、从下列条件中任选一个作为已知条件后,试判断四边形的形状,并证明你的结论.① , ② .
(1)、求证:;(2)、从下列条件中任选一个作为已知条件后,试判断四边形的形状,并证明你的结论.① , ② .选择的条件: ▲ (填写序号).(注:如果选择①,②分别进行解答,按第一个解答计分)
23. 冬天来了,为了晾晒衣服,小明在自家前院地面上立两根等长的立柱(均与地面垂直),并在立柱之间悬挂一根绳子,按如图所示的直角坐标系,绳子的形状可以近似地用抛物线来表示,如图(1),已知 , 绳子最低点与地面的距离为1.4m. (1)、求立柱的长度;(2)、由于晾晒的衣服比较多,为了防止衣服碰到地面,小明用一根垂直于地面的立柱撑起绳子,如图,的长度为1.65m,通过调整的位置,使左边抛物线对应的函数关系式为 , 最低点离地面1.49米,求水平距离 .24. 如图,在等边中, , 动点P从点A出发,沿方向运动;动点Q同时从点C出发,沿的延长线方向运动,当点P到达点B时,动点P,Q同时停止运动,Q,P两点的运动速度均为1cm/s,过点P作 , 垂足为D, , 相交于点E,设运动的时间为t(s) .
(1)、求立柱的长度;(2)、由于晾晒的衣服比较多,为了防止衣服碰到地面,小明用一根垂直于地面的立柱撑起绳子,如图,的长度为1.65m,通过调整的位置,使左边抛物线对应的函数关系式为 , 最低点离地面1.49米,求水平距离 .24. 如图,在等边中, , 动点P从点A出发,沿方向运动;动点Q同时从点C出发,沿的延长线方向运动,当点P到达点B时,动点P,Q同时停止运动,Q,P两点的运动速度均为1cm/s,过点P作 , 垂足为D, , 相交于点E,设运动的时间为t(s) . (1)、当t为何值时,为直角三角形?(2)、设四边形的面积为S(cm),写出S与t的关系式;(3)、在运动的过程中,是否存在某一时刻t,使?若存在,请求出t的值,若不存在,请说明理由,(4)、试判断之间有怎样的数量关系?请说明理由.
(1)、当t为何值时,为直角三角形?(2)、设四边形的面积为S(cm),写出S与t的关系式;(3)、在运动的过程中,是否存在某一时刻t,使?若存在,请求出t的值,若不存在,请说明理由,(4)、试判断之间有怎样的数量关系?请说明理由.