山东省青岛市即墨区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 如图所示的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、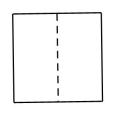 D、
D、 2. 一元二次方程x2﹣2x+3=0根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断3. 为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中正确的是( )
2. 一元二次方程x2﹣2x+3=0根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断3. 为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,大鱼与小鱼是关于原点O的位似图形,则下列说法中正确的是( )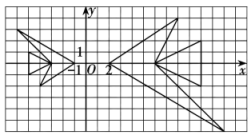 A、大鱼与小鱼的相似比是 B、小鱼与大鱼的对应点到位似中心的距离比是 C、大鱼尾巴的面积是小鱼尾巴面积的4倍 D、若小鱼上一点的坐标是 , 则在大鱼上的对应点的坐标是5. 在平面直角坐标系中,将抛物线向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、 B、 C、 D、6. 如图,在 中, ,则 sinB 的值为( )
A、大鱼与小鱼的相似比是 B、小鱼与大鱼的对应点到位似中心的距离比是 C、大鱼尾巴的面积是小鱼尾巴面积的4倍 D、若小鱼上一点的坐标是 , 则在大鱼上的对应点的坐标是5. 在平面直角坐标系中,将抛物线向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、 B、 C、 D、6. 如图,在 中, ,则 sinB 的值为( )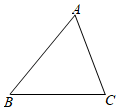 A、 B、 C、 D、7. 如图.在平面直角坐标系中,△AOB的面积为 ,BA垂直x轴于点A,OB与双曲线y= 相交于点C,且BC∶OC=1∶2,则k的值为( )
A、 B、 C、 D、7. 如图.在平面直角坐标系中,△AOB的面积为 ,BA垂直x轴于点A,OB与双曲线y= 相交于点C,且BC∶OC=1∶2,则k的值为( )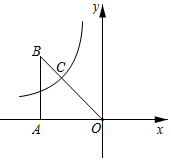 A、﹣3 B、﹣ C、3 D、8. 一次函数与二次函数在同一平面直角坐标系中的图像可能是( )A、
A、﹣3 B、﹣ C、3 D、8. 一次函数与二次函数在同一平面直角坐标系中的图像可能是( )A、 B、
B、 C、
C、 D、
D、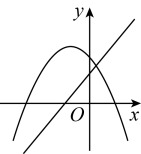
二、填空题
-
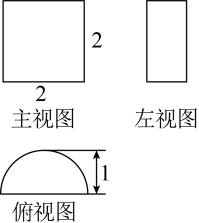
9. 在△ABC中,∠B=45°,cosA= , 则∠C的度数是 .10. 黄金分割在生活中的应用十分广泛,例如大多数窗户的宽和长的比是黄金比,已知某扇窗户的长为1.8米,则宽约为米.(结果精确到0.1)11. 已知反比例函数 ,当 时,y的取值范围为.12. 一个几何体的三视图如图所示,则该几何体的体积为 .
 13. 如图,在平行四边形中,E为边上的中点,交于点O,若 , 则平行四边形的面积为 .
13. 如图,在平行四边形中,E为边上的中点,交于点O,若 , 则平行四边形的面积为 . 14. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)
14. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)
三、解答题
-
15. 已知:如图,为直角,点D为射线上一点.
求作:矩形 , 使线段为矩形的一条边, , 且点F在的内部.
 16.(1)、解方程:(2)、已知二次函数的图象与x轴有交点,求a的取值范围.17. 为决定谁获得仅有的一张电影票,甲和乙设计了如下的游戏:在三张完全相同的卡片上分别写上字母A,B,B,背面朝上,每次抽取之前先洗匀,甲说:“我随机抽取一张,抽到字母B,电影票归我.”乙说:“我随机抽取一张后放回,再随机抽取一张,若两次抽取的字母相同,电影票归我.”试问:此游戏对谁更有利?并说明理由.18. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图(1)所示的坡路进行改造.如图(2)所示,改造前的斜坡的高度米,坡角;将斜坡的高度降低20米后,斜坡改造为斜坡 , 其坡度为1:4,改造后的斜坡多占多长一段地面?(结果保留根号)
16.(1)、解方程:(2)、已知二次函数的图象与x轴有交点,求a的取值范围.17. 为决定谁获得仅有的一张电影票,甲和乙设计了如下的游戏:在三张完全相同的卡片上分别写上字母A,B,B,背面朝上,每次抽取之前先洗匀,甲说:“我随机抽取一张,抽到字母B,电影票归我.”乙说:“我随机抽取一张后放回,再随机抽取一张,若两次抽取的字母相同,电影票归我.”试问:此游戏对谁更有利?并说明理由.18. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图(1)所示的坡路进行改造.如图(2)所示,改造前的斜坡的高度米,坡角;将斜坡的高度降低20米后,斜坡改造为斜坡 , 其坡度为1:4,改造后的斜坡多占多长一段地面?(结果保留根号)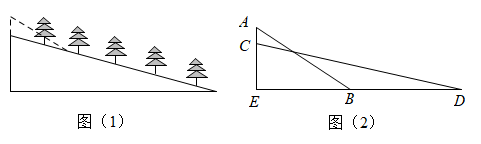 19. 如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
19. 如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度. 20. 某商场购进一批进货价为16元的日用品,销售一段时间后,为了获得更多的利润,商店决定提高价格.调查发现,若按每件20元的价格销售,每月能卖出360件,若按每件25元的价格销售,每月能卖210件,假定每月销售量y(件)是销售价格x(元/件)的一次函数.(1)、求y与x之间的关系式;(2)、销售价定为多少元时,该商场每月获得利润最大?最大利润是多少?21. 如图,是的角平分线, , , 垂足分别是E、F,连接 , 与相交千点H.
20. 某商场购进一批进货价为16元的日用品,销售一段时间后,为了获得更多的利润,商店决定提高价格.调查发现,若按每件20元的价格销售,每月能卖出360件,若按每件25元的价格销售,每月能卖210件,假定每月销售量y(件)是销售价格x(元/件)的一次函数.(1)、求y与x之间的关系式;(2)、销售价定为多少元时,该商场每月获得利润最大?最大利润是多少?21. 如图,是的角平分线, , , 垂足分别是E、F,连接 , 与相交千点H. (1)、求证:;(2)、满足什么条件时,四边形是正方形?说明理由.22. 某著名索拉桥,在桥头立柱两侧拉着钢索,以其中一根立柱为y轴,以桥面为x轴建立平面直角坐标系,如下图所示,左侧钢索近似于直线,底端在远离立柱200米的桥面上的B处固定,C处离桥面100米.右侧钢索近似于抛物线,该抛物线最低处A离立柱300米,离桥面10米.
(1)、求证:;(2)、满足什么条件时,四边形是正方形?说明理由.22. 某著名索拉桥,在桥头立柱两侧拉着钢索,以其中一根立柱为y轴,以桥面为x轴建立平面直角坐标系,如下图所示,左侧钢索近似于直线,底端在远离立柱200米的桥面上的B处固定,C处离桥面100米.右侧钢索近似于抛物线,该抛物线最低处A离立柱300米,离桥面10米. (1)、求出抛物线和直线的函数关系式;(不要求写自变量的取值范围)(2)、现要在左右两条钢索上各加一条竖直钢索和进行加固,要求它们的水平距离相距200米,请问这两条竖直钢索和加在何处,使得它们的高度之和最小?高度之和最小是多少?23. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数的图象,并探究该函数性质.(1)、绘制函数图象
(1)、求出抛物线和直线的函数关系式;(不要求写自变量的取值范围)(2)、现要在左右两条钢索上各加一条竖直钢索和进行加固,要求它们的水平距离相距200米,请问这两条竖直钢索和加在何处,使得它们的高度之和最小?高度之和最小是多少?23. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数的图象,并探究该函数性质.(1)、绘制函数图象①列表:下列是x与y的几组对应值,其中a= ▲ .
x
……
-5
-4
-3
-2
-1
1
2
3
4
5
……
y
……
-3.8
-2.5
-1
1
5
5
a
-1
-2.5
-3.8
……
②描点:根据表中的数值描点(x,y),请补充描出点(2,a);
③连线:请用平滑的曲线顺次连接各点,画出函数图象;
 (2)、探究函数性质,请写出函数y=-|x|的一条性质:;(3)、运用函数图象及性质
(2)、探究函数性质,请写出函数y=-|x|的一条性质:;(3)、运用函数图象及性质①写出方程-|x|=5的解;
②写出不等式-|x|≤1的解集 .
24. 如图,在菱形中, , 对角线 . 动点P从点A出发,以1cm/s的速度沿匀速运动;动点Q同时从点D出发,以2cm/s的速度沿的延长线方向匀速运动.当点P到达点B时,点P,Q同时停止运动.设运动时间为 , 过点P作 , 交于点E,以为边作平行四边形 , 连接 .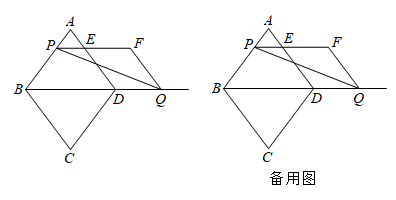 (1)、当t为何值时,E为的中点?(2)、当t为何值时,为直角三角形?(3)、设四边形的面积为 , 求S与t之间的函数关系式;(4)、是否存在某一时刻t,使点F在的平分线上?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,E为的中点?(2)、当t为何值时,为直角三角形?(3)、设四边形的面积为 , 求S与t之间的函数关系式;(4)、是否存在某一时刻t,使点F在的平分线上?若存在,求出t的值;若不存在,请说明理由.