辽宁省沈阳市浑南区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 关于x的一元二次方程的一个根是0,则a的值是( )A、0 B、4 C、-4 D、4或-42. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 一元二次方程根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、没有实数根 D、有两个不相等的实数根4. 圆的面积公式S=πR2中,S与R之间的关系是( )A、S是R的正比例函数 B、S是R的一次函数 C、S是R的二次函数 D、以上答案都不对5. 下列各种现象属于中心投影的是( )A、晚上人走在路灯下的影子 B、中午用来乘凉的树影 C、上午人走在路上的影子 D、阳光下旗杆的影子6. 某校男生中,若随机抽取若干名同学做“是否喜欢足球”的问卷调查,抽到喜欢足球的同学的概率是 ,这个 的含义是( ).A、只发出5份调查卷,其中三份是喜欢足球的答卷; B、在答卷中,喜欢足球的答卷与总问卷的比为3∶8; C、在答卷中,喜欢足球的答卷占总答卷的 ; D、在答卷中,每抽出100份问卷,恰有60份答卷是不喜欢足球.7. 二次函数的图像经过点 , , 则关于x的方程的根是( )A、 , B、 , C、 , D、 ,8. 菱形、矩形、正方形都具有的性质是( )A、对角线相等且互相平分 B、对角线相等且互相垂直 C、对角线互相平分 D、四条边相等9. 在平面直角坐标系中,与位似,位似中心是原点O,若 , 则与的周长比是( )
3. 一元二次方程根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、没有实数根 D、有两个不相等的实数根4. 圆的面积公式S=πR2中,S与R之间的关系是( )A、S是R的正比例函数 B、S是R的一次函数 C、S是R的二次函数 D、以上答案都不对5. 下列各种现象属于中心投影的是( )A、晚上人走在路灯下的影子 B、中午用来乘凉的树影 C、上午人走在路上的影子 D、阳光下旗杆的影子6. 某校男生中,若随机抽取若干名同学做“是否喜欢足球”的问卷调查,抽到喜欢足球的同学的概率是 ,这个 的含义是( ).A、只发出5份调查卷,其中三份是喜欢足球的答卷; B、在答卷中,喜欢足球的答卷与总问卷的比为3∶8; C、在答卷中,喜欢足球的答卷占总答卷的 ; D、在答卷中,每抽出100份问卷,恰有60份答卷是不喜欢足球.7. 二次函数的图像经过点 , , 则关于x的方程的根是( )A、 , B、 , C、 , D、 ,8. 菱形、矩形、正方形都具有的性质是( )A、对角线相等且互相平分 B、对角线相等且互相垂直 C、对角线互相平分 D、四条边相等9. 在平面直角坐标系中,与位似,位似中心是原点O,若 , 则与的周长比是( ) A、1:2 B、2:3 C、3:2 D、9:410. 已知二次函数的图像如图所示,则下列选项中正确的是( )
A、1:2 B、2:3 C、3:2 D、9:410. 已知二次函数的图像如图所示,则下列选项中正确的是( )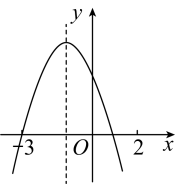 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 ,则 = .12. 将二次函数的图像向下平移5个单位长度,所得图像对应的函数表达式为 .13. 某工程队计划修建铁路,给出了铺轨的天数y(d)与每日铺轨量x(km/d)之间的关系表:
y(d)
120
150
200
240
300
x(km/d)
10
8
6
5
4
根据表格信息,判断出y是x的函数,则这个函数表达式是 .
14. 如图,在给定的一张平行四边形纸片上,用尺规作出四边形 , 具体作法如下:分别作的平分线 , 分别交于 , 连接 , 若 , 则四边形的周长是 . 15. 如图所示,某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度,他们通过调整测量位置,使斜边与地面保持平行,并使边与旗杆顶点在同一直线上,已知米,米,目测点到地面的距离米,到旗杆水平的距离米,则旗杆的高度为米.
15. 如图所示,某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度,他们通过调整测量位置,使斜边与地面保持平行,并使边与旗杆顶点在同一直线上,已知米,米,目测点到地面的距离米,到旗杆水平的距离米,则旗杆的高度为米. 16. 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C,D分别落在边BC下方的点C′,D′处,且点C′,D′,B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为(用含t的代数式表示).
16. 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C,D分别落在边BC下方的点C′,D′处,且点C′,D′,B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为(用含t的代数式表示).
三、解答题
-
17. 解方程: .18. 教育部在中小学部署了“从小学党史,永远跟党走”主题教育活动.学校开展了“童心向党”的大赛活动,最后决赛环节由组委会提供“A组:图话百年”“B组:动听百年”“C组:话说当年”三组题目,将依次代表三组题目的A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.甲、乙两名同学进入了决赛环节,比赛时甲先从中随机抽取一张卡片,记录下卡片上的字母,放回后洗匀,再由乙从中随机抽取一张卡片,两人按各自抽取的卡片上的字母回答相应题组中的问题.(1)、请直接写出同学甲摸到“B组:动听百年”中问题的概率;(2)、请利用画树状图或列表的方法求甲、乙两名同学抽到的题目不在同一题组的概率.19. 义务教育劳动课程以丰富开放的劳动项目为载体.学校准备在校园内利用校围墙的一段(墙体的最大可用长度a=10米)和篱笆,围成中间隔有一道篱笆的矩形劳动实践菜园(如图),已知篱笆长24米(篱笆全部用完),如果要围成面积为45平方米的菜园,的长是多少米?
 20. 如图,点A,点C在反比例函数图象上,点C在点A下方,且点C坐标为 , 连接OA,OC,过点A作轴交于点B,点B的纵坐标为 .
20. 如图,点A,点C在反比例函数图象上,点C在点A下方,且点C坐标为 , 连接OA,OC,过点A作轴交于点B,点B的纵坐标为 . (1)、填空:k= , 点A的坐标为;(2)、观察图象,当时,请直接写出自变量x的取值范围;(3)、连接AC,请直接写出的面积.21. 如图,菱形ABCD的对角线AC和BD相交于点O,于点E交AC于点P,于点F.
(1)、填空:k= , 点A的坐标为;(2)、观察图象,当时,请直接写出自变量x的取值范围;(3)、连接AC,请直接写出的面积.21. 如图,菱形ABCD的对角线AC和BD相交于点O,于点E交AC于点P,于点F. (1)、判断四边形DEBF的形状,并说明理由;(2)、如果 , , 求出DP的长.22. 驻村扶贫小组实施产业扶贫,帮助贫困农户进行农作物种植和销售.已知某农产品成本为每千克10元.经过市场调研发现,如果销售单价为14元,每天可销售160千克,销售单价每增加1元,销售量就减少10千克.设每天销售量为y千克,销售单价为x元().(1)、请直接用含x代数式表示y;(2)、设每天的销售利润为W(元),
(1)、判断四边形DEBF的形状,并说明理由;(2)、如果 , , 求出DP的长.22. 驻村扶贫小组实施产业扶贫,帮助贫困农户进行农作物种植和销售.已知某农产品成本为每千克10元.经过市场调研发现,如果销售单价为14元,每天可销售160千克,销售单价每增加1元,销售量就减少10千克.设每天销售量为y千克,销售单价为x元().(1)、请直接用含x代数式表示y;(2)、设每天的销售利润为W(元),①求销售利润W与x之间的函数关系式;
②将销售单价定为多少时,才能使每天的销售利润W最大,最大利润是多少?
23. 如图1,在平面直角坐标系中,矩形OABC的邻边分别落在x轴,y轴的正半轴上,且顶点O与原点重合, , , 连接 , 点E由点B出发沿方向向点O匀速运动,速度为;点F由点O出发沿方向向点A匀速运动,速度为 , 点E,F同时出发,其中一点到达终点时,另一点也停止运动,设运动时间为t(s),连接EF.回答下列问题: (1)、填空:点B的坐标;用含t的代数式表示OE的长;(2)、如图2,连接AC,交OB于点D,连接DF,若 , 求点E的坐标;(3)、连接 , 把沿翻折,点E的对应点为 , 得到四边形 . 当四边形为菱形时,请直接写出t的值.24. 四边形是边长为4的正方形,点E沿A→D→C路线向C点运动,连接 , 在的右侧以为腰作等腰直角三角形 , , 交射线于点N.
(1)、填空:点B的坐标;用含t的代数式表示OE的长;(2)、如图2,连接AC,交OB于点D,连接DF,若 , 求点E的坐标;(3)、连接 , 把沿翻折,点E的对应点为 , 得到四边形 . 当四边形为菱形时,请直接写出t的值.24. 四边形是边长为4的正方形,点E沿A→D→C路线向C点运动,连接 , 在的右侧以为腰作等腰直角三角形 , , 交射线于点N.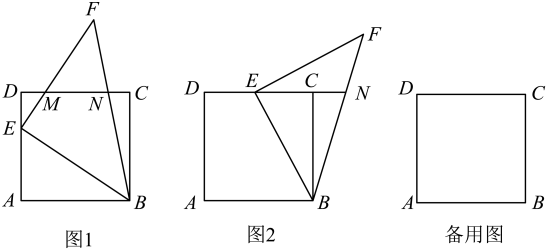 (1)、如图1,点E在上时,交于点M,若 , 请直接写出:
(1)、如图1,点E在上时,交于点M,若 , 请直接写出:①点F到直线的距离;
②的长;
(2)、如图2,点E在上时,①若 , 求的长;
②连接 , 请直接写出的最小值.
25. 如图1,平面直角坐标系中,O是坐标原点,二次函数的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点 , 点B坐标是 , 点P是抛物线的顶点. (1)、请直接写出二次函数的表达式及顶点P的坐标;(2)、如图2,设二次函数图象的对称轴与x轴交于点H,
(1)、请直接写出二次函数的表达式及顶点P的坐标;(2)、如图2,设二次函数图象的对称轴与x轴交于点H,①连接 , 点D为对称轴上的一点,且与相似,求点D的坐标;
②点M为对称轴PH上一点且在x轴下方,在x轴负半轴上有一点E,在y轴负半轴上有一点F,且满足 , 已知点N在抛物线上,以E,F,M,N为顶点的四边形为平行四边形,请直接写出点E的坐标.