辽宁省大连市中山区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 下列与2022年冬奥会相关的图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 书架上有1本数学书,2本物理书.从中任取1本书是物理书的概率为( )A、 B、 C、 D、3. 已知甲、乙两地相距s(单位:km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(单位:h)关于行驶速度v(单位:km/h)的函数图象是( )A、
2. 书架上有1本数学书,2本物理书.从中任取1本书是物理书的概率为( )A、 B、 C、 D、3. 已知甲、乙两地相距s(单位:km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(单位:h)关于行驶速度v(单位:km/h)的函数图象是( )A、 B、
B、 C、
C、 D、
D、 4. 已知 ,则 ( )A、2 B、 C、3 D、5. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、6. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( )
4. 已知 ,则 ( )A、2 B、 C、3 D、5. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、6. 如图,在△ABC中,DE∥AB,且 = ,则 的值为( ) A、 B、 C、 D、7. 如图,AB是⊙O的直径,AC,BC是⊙O的弦,若 ,则 的度数为( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,AC,BC是⊙O的弦,若 ,则 的度数为( )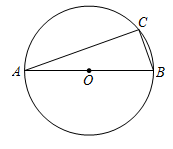 A、70° B、90° C、40° D、60°8. 如图,与位似,点O是它们的位似中心,且位似比为1∶2,则与的周长之比是( )
A、70° B、90° C、40° D、60°8. 如图,与位似,点O是它们的位似中心,且位似比为1∶2,则与的周长之比是( ) A、1∶2 B、1∶4 C、1∶3 D、1∶99. 如图,已知正五边形内接于 , 连接 , 则的度数是( )
A、1∶2 B、1∶4 C、1∶3 D、1∶99. 如图,已知正五边形内接于 , 连接 , 则的度数是( ) A、72° B、54° C、36° D、30°10. 已知抛物线上的部分点的横坐标与纵坐标的对应值如表:
A、72° B、54° C、36° D、30°10. 已知抛物线上的部分点的横坐标与纵坐标的对应值如表:…
-1
0
1
2
3
…
…
3
0
-1
3
…
以下结论错误的是( )
A、抛物线的顶点坐标为 B、当时,y随x增大而增大 C、方程的根为0和2 D、当时,的取值范围是二、填空题
-
11. 在一个不透明的口袋中装有红球和白球共30个,这些球除颜色外都相同,将口袋中的球搅匀后,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有20次摸到红球,则口袋中红球的个数约为 .12. 反比例函数的图像的两个分支分别位于第二,四象限,则的取值范围是 .13. 如图,将绕点O按逆时针方向旋转55°后得到 , 若 , 则的度数是 .
 14. 如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高m,测得m,m.则建筑物的高是m.
14. 如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高m,测得m,m.则建筑物的高是m.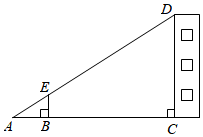 15. 如图,B为外一点,与相切于点A, , , 则长为 .
15. 如图,B为外一点,与相切于点A, , , 则长为 . 16. 一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 . 则他将铅球推出的成绩是 m.
16. 一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 . 则他将铅球推出的成绩是 m.三、解答题
-
17. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
 (1)、画出绕点O逆时针旋转90°后的;(2)、点的坐标为 , 点的坐标为 , 点的坐标为 .18. 如图,两个圆都以点O为圆心,大圆的弦交小圆于C,D两点, . 求的长.
(1)、画出绕点O逆时针旋转90°后的;(2)、点的坐标为 , 点的坐标为 , 点的坐标为 .18. 如图,两个圆都以点O为圆心,大圆的弦交小圆于C,D两点, . 求的长. 19. 已知反比例函数的图象经过点 .(1)、求这个反比例函数的表达式;(2)、当时,求的取值范围.20. 已知抛物线的解析式为 , 将抛物线先向右平移1个单位长度,再向下平移2个单位长度得到抛物线 .(1)、求抛物线的函数关系式;(2)、点能否在抛物线上?请说明理由.21. 一个不透明的口袋中有四个完全不相同的小球,把它们分别标号为1,2,3,4.(1)、随机摸取一个小球,标号是2的概率为;(2)、随机摸取一个小球然后放回,再随机摸取一个小球,请用列表法(或树状图)求两次取出的小球标号的和为4的概率.22. 如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.设矩形的面积为 . 问长为多少时S最大,并求最大面积.
19. 已知反比例函数的图象经过点 .(1)、求这个反比例函数的表达式;(2)、当时,求的取值范围.20. 已知抛物线的解析式为 , 将抛物线先向右平移1个单位长度,再向下平移2个单位长度得到抛物线 .(1)、求抛物线的函数关系式;(2)、点能否在抛物线上?请说明理由.21. 一个不透明的口袋中有四个完全不相同的小球,把它们分别标号为1,2,3,4.(1)、随机摸取一个小球,标号是2的概率为;(2)、随机摸取一个小球然后放回,再随机摸取一个小球,请用列表法(或树状图)求两次取出的小球标号的和为4的概率.22. 如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.设矩形的面积为 . 问长为多少时S最大,并求最大面积.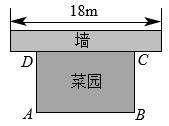 23. 如图1,A,P,B,C是上的四个点, .
23. 如图1,A,P,B,C是上的四个点, . (1)、若 , 判断的形状,并证明你的结论;(2)、如图2,若CP是的直径, , 交于点E,过点A的切线交的延长线于点Q,若 , , 求的值.24. 如图,在中, , , , 点D在 上,且 , 点E是边上一动点(点E不与点A,C重合),过点E作 , 垂足为点F,设 , 与重叠部分的面积为S.
(1)、若 , 判断的形状,并证明你的结论;(2)、如图2,若CP是的直径, , 交于点E,过点A的切线交的延长线于点Q,若 , , 求的值.24. 如图,在中, , , , 点D在 上,且 , 点E是边上一动点(点E不与点A,C重合),过点E作 , 垂足为点F,设 , 与重叠部分的面积为S. (1)、求的长;(2)、求S与x的函数关系式,并直接写出自变量的取值范围.25. 综合与实践
(1)、求的长;(2)、求S与x的函数关系式,并直接写出自变量的取值范围.25. 综合与实践
问题情境:数学活动课上,李老师出示了一个问题:
如图1,在中,点E,D分别在边AB,AC上,连接DE, .
求证: .
(1)、独立思考:请解答李老师提出的问题.(2)、实践探究:在原有问题条件不变的情况下,李老师增加下面的条件,并提出新问题,请你解答.“如图2,延长CA至点F,使 , 连接BF.延长DE交BF于点H,且 . 在图中找出与相等的线段,并证明.”
(3)、问题解决:数学活动小组同学对上述问题进行特殊化研究之后发现,当时,若给出中任意两边长,则图3中所有已经用字母标记的线段长均可求.该小组提出下面的问题,请你解答.“如图3,在(2)的条件下,若 , , , 求的长.”
26. 如图1,抛物线与x轴交于点A,B,与y轴交于点C,点B坐标为 , 点D为线段OB上一点,点E为抛物线上一动点. (1)、求b的值;(2)、点D坐标为(3,0),点E在第一象限的抛物线上,设的面积为S,求S的最大值;(3)、如图2,点D坐标为(4,0),是否存在点E,使 , 若存在,请求出点E坐标,若不存在,说明理由.
(1)、求b的值;(2)、点D坐标为(3,0),点E在第一象限的抛物线上,设的面积为S,求S的最大值;(3)、如图2,点D坐标为(4,0),是否存在点E,使 , 若存在,请求出点E坐标,若不存在,说明理由.