吉林省白城市大安市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 任意转动如图的指针,指针( )
2. 任意转动如图的指针,指针( )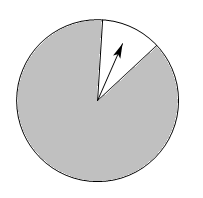 A、一定停在黑色区域 B、很有可能停在黑色区域 C、偶尔停在黑色区域 D、不可能停在黑色区域3. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
A、一定停在黑色区域 B、很有可能停在黑色区域 C、偶尔停在黑色区域 D、不可能停在黑色区域3. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )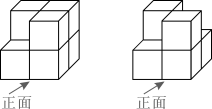 A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同4. 在二次函数的图像中,若y随x的增大而增大,则x的取值范围是( )A、x≤-1 B、x≥-1 C、x≤1 D、x≥15. 如图,已知四边形ABCD内接于⊙O,∠A=100°,则∠BOD=( )
A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同4. 在二次函数的图像中,若y随x的增大而增大,则x的取值范围是( )A、x≤-1 B、x≥-1 C、x≤1 D、x≥15. 如图,已知四边形ABCD内接于⊙O,∠A=100°,则∠BOD=( ) A、80° B、50° C、160° D、100°6. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )
A、80° B、50° C、160° D、100°6. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )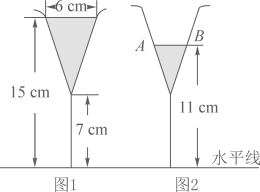 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 一元二次方程 的解为.8. 计算:tan60°-sin60°= .9. 用配方法将抛物线化成顶点式得 .10. 如图,直线a∥b∥c,它们依次交直线m,n于点A、C、E和B、D、F,已知AC=4,CE=6,BD=3,那么BF等于 .
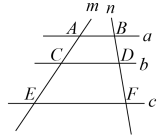 11. 如图,将△ABC绕点A顺时针旋转60°得到△AED . 若线段AB=3,则△ABE的周长等于 .
11. 如图,将△ABC绕点A顺时针旋转60°得到△AED . 若线段AB=3,则△ABE的周长等于 .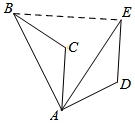 12. 某商品经过两次连续降价,每件售价由原来的60元降到了40元.设平均每次降价的百分率为x,则可列方程是 .13. 一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=100m3时,ρ=1.4kg/m3;那么当V=2m3时,氧气的密度为kg/m3.14. 如图,将正方形绕着点逆时针旋转得到正方形 , 点的对应点落在正方形的对角线上,若 , 则的长为 .
12. 某商品经过两次连续降价,每件售价由原来的60元降到了40元.设平均每次降价的百分率为x,则可列方程是 .13. 一定质量的氧气,它的密度ρ(kg/m3)是它的体积V(m3)的反比例函数,当V=100m3时,ρ=1.4kg/m3;那么当V=2m3时,氧气的密度为kg/m3.14. 如图,将正方形绕着点逆时针旋转得到正方形 , 点的对应点落在正方形的对角线上,若 , 则的长为 .
三、解答题
-
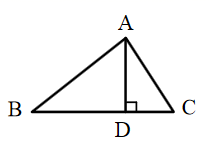
15. 解方程:(x+5)(x-2)=1.16. 关于x的一元二次方程有实数根.(1)、当是方程的一个根,求m的值;(2)、求m的取值范围.17. 四张大小、质地均相同的卡片上分别标有数字1,2,3,4,现将标有数字的一面朝下扣在桌子上,从中随机抽取一张,再从剩下的三张中随机抽取一张.用列表或画树状图的方法,求抽得的两张卡片上的数字之积为奇数的概率.18. 如图,在 中, ,AD是BC边上的高,若 , ,求AC的长.
 19. 按要求画图.
19. 按要求画图. (1)、画出图①的另一半,使它成为一个轴对称图形.(2)、画出图②绕O点按顺时针旋转90°后的图形.(3)、画出图③按1:2缩小后的图形.20. 如图,点O为中点,分别延长到点C,到点D,使 . 以点O为圆心,分别以 , 为半径在上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接并延长交大半圆于点E,连接 , .
(1)、画出图①的另一半,使它成为一个轴对称图形.(2)、画出图②绕O点按顺时针旋转90°后的图形.(3)、画出图③按1:2缩小后的图形.20. 如图,点O为中点,分别延长到点C,到点D,使 . 以点O为圆心,分别以 , 为半径在上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接并延长交大半圆于点E,连接 , . (1)、求证:;(2)、若 , 当最大时,直接指出与小半圆的位置关系,并求此时(答案保留π).21. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆” , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高米,“标杆”米,又米,米.
(1)、求证:;(2)、若 , 当最大时,直接指出与小半圆的位置关系,并求此时(答案保留π).21. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆” , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高米,“标杆”米,又米,米.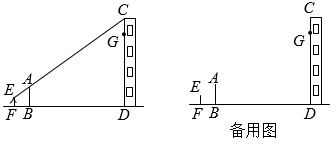 (1)、求大楼的高度为多少米(垂直地面)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼上点G的高度米,那么相对于第一次测量,标杆应该向大楼方向移动米.22. 如图,在中点P从A点开始沿边向点B以1cm/秒的速度移动,同时点Q从B点开始沿边向点C以2cm/秒的速度移动,且当其中一点到达终点时,另一个点随之停止移动.设P,Q两点移动的时间为t秒,的面积为 .
(1)、求大楼的高度为多少米(垂直地面)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼上点G的高度米,那么相对于第一次测量,标杆应该向大楼方向移动米.22. 如图,在中点P从A点开始沿边向点B以1cm/秒的速度移动,同时点Q从B点开始沿边向点C以2cm/秒的速度移动,且当其中一点到达终点时,另一个点随之停止移动.设P,Q两点移动的时间为t秒,的面积为 .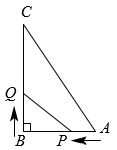 (1)、cm;(2)、求S与t的函数关系式,并求出面积的最大值.23. 光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率(α代表入射角,β代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验:通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块.图③是实验的示意图,点A,C,B在同一直线上,测得 , , , 求光线从空气射入水中的折射率n.
(1)、cm;(2)、求S与t的函数关系式,并求出面积的最大值.23. 光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率(α代表入射角,β代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验:通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块.图③是实验的示意图,点A,C,B在同一直线上,测得 , , , 求光线从空气射入水中的折射率n. 24. 如图,和中,交于M.
24. 如图,和中,交于M. (1)、如图1,当时,的度数为°;(2)、如图2,当时,求的度数为°;(3)、如图3,当绕O点任意旋转时,与是否存在着确定的数量关系?如果存在,请你用表示 , 并用图3进行证明;若不确定,说明理由.25. 如图,在平面直角坐标系中,点A,B分别是y轴和x轴的正半轴上的动点,正方形的顶点C,D在第一象限.
(1)、如图1,当时,的度数为°;(2)、如图2,当时,求的度数为°;(3)、如图3,当绕O点任意旋转时,与是否存在着确定的数量关系?如果存在,请你用表示 , 并用图3进行证明;若不确定,说明理由.25. 如图,在平面直角坐标系中,点A,B分别是y轴和x轴的正半轴上的动点,正方形的顶点C,D在第一象限. (1)、当 , 时,正方形的顶点D恰好在反比例函数(k为常数,)的图象上,求k的值;(2)、保持不变,移动点A,B,使 , 求此时点D的坐标,并判断点D是否在(1)中的反比例函数图象上.26. 如图,在平面直角坐标系中,抛物线与x轴交于点 , 抛物线的对称轴l经过点B,且点B在抛物线上,作直线 . P是该抛物线上一点,过点P作x轴的垂线交于点Q,过点P作于点N,以为边作矩形 .
(1)、当 , 时,正方形的顶点D恰好在反比例函数(k为常数,)的图象上,求k的值;(2)、保持不变,移动点A,B,使 , 求此时点D的坐标,并判断点D是否在(1)中的反比例函数图象上.26. 如图,在平面直角坐标系中,抛物线与x轴交于点 , 抛物线的对称轴l经过点B,且点B在抛物线上,作直线 . P是该抛物线上一点,过点P作x轴的垂线交于点Q,过点P作于点N,以为边作矩形 . (1)、求b的值;(2)、当点P在抛物线A,B两点之间时,求线段长度的最大值;(3)、矩形与此抛物线相交,抛物线被截得的部分图象记作G,G的最高点的纵坐标为m,最低点纵坐标为n.当时,直接写出点P的坐标.
(1)、求b的值;(2)、当点P在抛物线A,B两点之间时,求线段长度的最大值;(3)、矩形与此抛物线相交,抛物线被截得的部分图象记作G,G的最高点的纵坐标为m,最低点纵坐标为n.当时,直接写出点P的坐标.