广东省阳江市阳春市2022-2023学年九年级上学期12月期末数学试题

试卷更新日期：2023-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中是必然事件的是（）

A、明天太阳从东方升起 B、投掷一枚均匀的硬币 $10$ 次，正面朝上的次数为 $5$ 次 C、射击运动员射击一次，命中靶心 D、平面内，任意一个五边形的外角和等于 $540 °$

查看试题解析
3. 在平面直角坐标系内，点A的坐标是（2，3），则点A关于原点中心对称点的坐标是（）

A、（﹣2，3） B、（﹣3，﹣2） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
4. 平面内，已知 $⊙ O$ 的半径为 $10 c m ， P O = 12 c m$ ，则点 $P$ 与 $⊙ O$ 的位置关系是（）

A、点 $P$ 在 $⊙ O$ 上 B、点 $P$ 在 $⊙ O$ 内 C、点 $P$ 在 $⊙ O$ 外 D、不能确定

查看试题解析
5. 已知现有的10瓶饮料中有2瓶已过了保质期，从这10瓶饮料中任取1瓶，恰好取到已过了保质期的饮料的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{9}{10}$ C、 $\frac{1}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 如图，AB是 $⊙ O$ 的弦，半径 $O C ⊥ A B$ 于点D，若 $⊙ O$ 的半径为10cm， $A B = 16 cm$ ，则OD的长是（）．

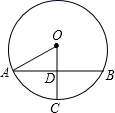A、3cm B、4cm C、5cm D、6cm

查看试题解析
7. 一元二次方程 $x^{2} - 3 x + 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、没有实数根

查看试题解析
8. 如图，点A，B，C均在 $⊙ O$ 上，若 $∠ A O B = 60 °$ ，则 $∠ A C B$ 的度数是（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
9. 将抛物线 $y = 3 x^{2}$ 向左平移2个单位，再向下平移5个单位，得到的抛物线是（）

A、 $y = 3 (x + 2)^{2} + 5$ B、 $y = 3 (x + 2)^{2} - 5$ C、 $y = 3 (x - 2)^{2} + 5$ D、 $y = 3 (x - 2)^{2} - 5$

查看试题解析
10. 已知点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 均在抛物线 $y = x^{2} - 1$ 上，下列说法正确的是（）

A、若 $x_{1} = - x_{2}$ ，则 $y_{1} = - y_{2}$ B、若 $y_{1} = y_{2}$ ，则 $x_{1} = x_{2}$ C、若 $x_{1} < x_{2} < 0$ ，则 $y_{1} < y_{2}$ D、若 $0 < x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$

查看试题解析

二、填空题

11. 已知 $x = 1$ 是关于x的一元二次方程 $x^{2} + x + 2 a = 0$ 的一个解，则a的值为．

查看试题解析
12. 抛物线 $y = 2 {(x - 3)}^{2} + 4$ 的对称轴是直线．

查看试题解析
13. 关于x的一元二次方程 $x^{2} + 4 x - m = 0$ 有两个实数根，则实数m的取值范围是．

查看试题解析
14. 在一个不透明的袋子中装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次实验发现，摸出黄球的频率稳定在0.30左右，则袋子中黄球的数量可能是个．

查看试题解析
15. 如图，扇形纸扇完全打开后，扇面（即扇形 $A B C$ ）的面积为 $135 π c m^{2}$ ，竹条 $A B$ ， $A C$ 的长均为 $18 c m$ ，则 $\overset{⌢}{B C}$ 的长为cm（结果保留 $π$ ）．

查看试题解析

三、解答题

16. 解方程： $x^{2} + 2 x - 2 = 0$ .

查看试题解析
17. 已知：△ABC在坐标平面内，三个顶点的坐标分别为 $A (0 ， 3)$ ， $B (3 ， 4)$ ， $C (2 ， 2)$ ．（正方形网格中，每个小正方形的边长是1个单位长度）
⑴ $Δ A_{1} B_{1} C_{1}$ 与△ABC关于原点O成中心对称，画出 $Δ A_{1} B_{1} C_{1}$ ；
⑵作出△ABC绕点A顺时针方向旋转 $90 °$ 后得到的 $Δ A_{2} B_{2} C_{2}$ ．

查看试题解析
18. 实施“双减”政策后，某校每周举行一次学科实践作业秀活动，内容有布艺、剪纸、卡通画（分别用A，B，C依次表示这三种作业）．小聪和小明计划每人选择一种作业，上述三种作业中的每一种作业被选中的可能性均相同．请你用列表法或画树状图法，求小聪和小明选择同一种作业的概率．

查看试题解析
19. 现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，某快递公司今年九月份与十一月份的投递总件数分别为10万件和12.1万件，该公司每月的投递总件数的增长率相同．求该快递公司投递总件数的月增长率．

查看试题解析
20. 如图，将 $△ A B C$ 绕点A顺时针旋转60°得到 $△ A E D$ ，

(1)、填空：若 $∠ B A C = 35 °$ ，则 $∠ C A E$ 的度数为；

(2)、连接 $B E$ ，若线段 $A B = 5$ ，求 $△ A B E$ 的周长．

查看试题解析
21. 如图，喷泉的喷头喷出的水珠在空中形成抛物线，在抛物线各个位置上水珠的竖直高度y（单位：m）与它喷头的水平距离x（单位：m）满足函数关系式 $y = - 2 x^{2} + 4 x + 6$ ．

(1)、求水珠运动过程中距离地面的最大高度；

(2)、观赏的人站在距离喷头水平距离 $3.5 m$ 的地方，会不会恰好被喷泉喷出的水打湿？请说明理由．

查看试题解析
22. 如图，点C在以 $A B$ 为直径的 $⊙ O$ 上， $B D$ 平分 $∠ A B C$ 交 $⊙ O$ 于点D，过D作 $B C$ 的垂线交 $B A$ 的延长线于点F，垂足为E．

(1)、求证： $D E$ 与 $⊙ O$ 相切；

(2)、若 $∠ A B C = 60 °$ ， $A F = 5$ ，求 $⊙ O$ 的半径．

查看试题解析
23. 在平面直角坐标系中，已知抛物线y＝ax²+bx-4经过A（-4，0），C（2，0）两点．

(1)、求抛物线的解析式；

(2)、若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．

查看试题解析