广东省阳江市江城区2022-2023学年九年级上学期期末质量监测数学试卷
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. “打开电视机,正在播放阳江新闻”这一事件是( )A、必然事件 B、不可能事件 C、确定性事件 D、随机事件2. 古希腊哲学家毕达哥拉斯曾说:“美的线型和其他一切美的形体,都必须有对称形式.”下面以数学家名字命名的图形中,是中心对称图形的是( )A、谢尔宾斯基三角形
 B、科克曲线
B、科克曲线 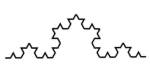 C、赵爽弦图
C、赵爽弦图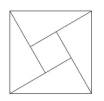 D、毕达哥拉斯树
D、毕达哥拉斯树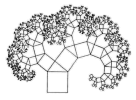 3. 若是一元二次方程的根,则的值为( )A、6 B、7 C、8 D、94. 抛物线的顶点坐标( )A、 B、 C、 D、5. 设方程的两根分别是、 , 则( )A、-3 B、2 C、-2 D、36. 将抛物线向左平移2个单位后得到的抛物线表达式是( )A、 B、 C、 D、7. 如图,是的直径,是的弦, , 则的度数是( )
3. 若是一元二次方程的根,则的值为( )A、6 B、7 C、8 D、94. 抛物线的顶点坐标( )A、 B、 C、 D、5. 设方程的两根分别是、 , 则( )A、-3 B、2 C、-2 D、36. 将抛物线向左平移2个单位后得到的抛物线表达式是( )A、 B、 C、 D、7. 如图,是的直径,是的弦, , 则的度数是( ) A、 B、 C、 D、8. 如图,小红利用小孔成像原理制作了一个成像装置,他在距离纸筒处准备了一支蜡烛,蜡烛长为 , 纸筒的长度为 , 则这支蜡烛所成像的高度为( )
A、 B、 C、 D、8. 如图,小红利用小孔成像原理制作了一个成像装置,他在距离纸筒处准备了一支蜡烛,蜡烛长为 , 纸筒的长度为 , 则这支蜡烛所成像的高度为( ) A、 B、 C、 D、9. 如图,将绕直角顶点顺时针旋转 , 得到 , 连接 , , 则的度数为( )
A、 B、 C、 D、9. 如图,将绕直角顶点顺时针旋转 , 得到 , 连接 , , 则的度数为( ) A、 B、 C、 D、71°10. 二次函数的部分图象如图所示,其对称轴为直线 , 且与轴的一个交点坐标为 , 下列结论:
A、 B、 C、 D、71°10. 二次函数的部分图象如图所示,其对称轴为直线 , 且与轴的一个交点坐标为 , 下列结论:①;②;③图象与轴的另一个交点坐标为;④关于的一元二次方程有两个相等的实数根;⑤ . 其中正确的结论个数是( )
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 在平面直角坐标系中,点关于原点对称的点的坐标是 .12. 点 , 在抛物线上,则 , 的大小关系为:(填“>”,“=”或“<”).13. 如图,矩形ABOC的顶点A在反比例函数()的图像上,矩形ABOC的面积为3,则k= .
 14. 如图,OM为半圆的直径,观察图中的尺规作图痕迹,若 , 则的度数为 .
14. 如图,OM为半圆的直径,观察图中的尺规作图痕迹,若 , 则的度数为 . 15. 如图,在扇形中,半径的长为2,点在弧上,连接 , , , 若四边形为菱形,则图中阴影部分的面积为 . (用含的代数式表示)
15. 如图,在扇形中,半径的长为2,点在弧上,连接 , , , 若四边形为菱形,则图中阴影部分的面积为 . (用含的代数式表示)
三、解答题
-
16. 解方程:.17. 已知反比例函数 .(1)、如果这个函数的图象经过点(2,-1),求k的值;(2)、如果在这个函数图象所在的每个象限内, y的值随x的值增大而减小,求k的取值范围.18. 如图,在平面直角坐标系中,每个小正方形的边长都为1个单位长度
 (1)、画出绕点顺时针旋转的图形;(2)、求出点的旋转路径长.19. 乌克兰危机发生之后,外交战线按照党中央的部署紧急行动,在战火粉飞中已将5200多名同胞安全从乌克兰撤离,电影《万里归途》正是“外交为民”的真实写照,如表是该影片票房的部分数据,(注:票房是指截止发布日期的所有售票累计收入)
(1)、画出绕点顺时针旋转的图形;(2)、求出点的旋转路径长.19. 乌克兰危机发生之后,外交战线按照党中央的部署紧急行动,在战火粉飞中已将5200多名同胞安全从乌克兰撤离,电影《万里归途》正是“外交为民”的真实写照,如表是该影片票房的部分数据,(注:票房是指截止发布日期的所有售票累计收入)影片《万里归途》的部分统计数据
发布日期
10月8日
10月11日
10月12日
发布次数
第1次
第2次
第3次
票房
10亿元
12.1亿元
(1)、平均每次累计票房增长的百分率是多少?(2)、在(1)的条件下,若票价每张40元,求10月11日卖出多少张电影票20. 第24届冬奥会期间,小星收集到4张卡片,按顺序分别记为卡片、、、 . 正面图案如图所示,卡片背面完全相同. (1)、若小星从中随机摸出一张卡片,则卡片上的图案恰好是花样滑冰的概率是 .(2)、小星把这4张卡片背面朝上洗匀后摸出1张,放回洗匀后再摸出一张,请用列表或画树状图的方法,求这两张卡片正面图案恰好是冰壶和冰球的概率.21. 如图,在矩形ABCD中,AB=2,BC=3,M是BC的中点,DE⊥AM于点E.
(1)、若小星从中随机摸出一张卡片,则卡片上的图案恰好是花样滑冰的概率是 .(2)、小星把这4张卡片背面朝上洗匀后摸出1张,放回洗匀后再摸出一张,请用列表或画树状图的方法,求这两张卡片正面图案恰好是冰壶和冰球的概率.21. 如图,在矩形ABCD中,AB=2,BC=3,M是BC的中点,DE⊥AM于点E. (1)、求证:△ADE∽△MAB;(2)、求DE的长.
(1)、求证:△ADE∽△MAB;(2)、求DE的长.

