广东省深圳市南山区2022-2023学年九年级上学期期末考试数学试卷
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 如图是一把做工精湛的紫砂壶“景舟石瓢”,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 若方程有两个不相等的实数根,则m的值可以是( )A、5 B、4 C、3 D、23. 已知反比例函数的图象经过点 , 则这个函数的图象位于( )A、第二、三象限 B、第一、三象限 C、第三、四象限 D、第二、四象限4. 如图,四边形ABCD的对角线AC与BD相交于点O,下列条件中,能判定四边形ABCD是矩形的是( )
2. 若方程有两个不相等的实数根,则m的值可以是( )A、5 B、4 C、3 D、23. 已知反比例函数的图象经过点 , 则这个函数的图象位于( )A、第二、三象限 B、第一、三象限 C、第三、四象限 D、第二、四象限4. 如图,四边形ABCD的对角线AC与BD相交于点O,下列条件中,能判定四边形ABCD是矩形的是( ) A、AB∥DC,AB=CD B、AB∥CD,AD∥BC C、AC=BD,AC⊥BD D、OA=OB=OC=OD5. 一个口袋中有红球、黄球共20个,这些除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一球,记下颜色后再放回口袋,不断重复这一过程,共摸了200次,发现其中有161次摸到红球.则这个口袋中红球数大约有( )A、4个 B、10个 C、16个 D、20个6. 如图,广场上有一盏路灯挂在高的电线杆顶上,记电线杆的底部为 . 把路灯看成一个点光源,一名身高的女孩站在点处, , 则女孩的影子长为( )
A、AB∥DC,AB=CD B、AB∥CD,AD∥BC C、AC=BD,AC⊥BD D、OA=OB=OC=OD5. 一个口袋中有红球、黄球共20个,这些除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一球,记下颜色后再放回口袋,不断重复这一过程,共摸了200次,发现其中有161次摸到红球.则这个口袋中红球数大约有( )A、4个 B、10个 C、16个 D、20个6. 如图,广场上有一盏路灯挂在高的电线杆顶上,记电线杆的底部为 . 把路灯看成一个点光源,一名身高的女孩站在点处, , 则女孩的影子长为( ) A、 B、 C、 D、7. 如图,长方形花圃面积为 , 它的一边利用已有的围墙(围墙足够长),另外三边所围的栅栏的总长度是 . 处开一门,宽度为 . 设的长度是 , 根据题意,下面所列方程正确的是( )
A、 B、 C、 D、7. 如图,长方形花圃面积为 , 它的一边利用已有的围墙(围墙足够长),另外三边所围的栅栏的总长度是 . 处开一门,宽度为 . 设的长度是 , 根据题意,下面所列方程正确的是( ) A、 B、 C、 D、8. 下面说法错误的是( )A、点 , 都在反比例函数图象上,且 , 则 B、若点是线段的黄金分割点, , , 则 C、顺次连接对角线互相垂直的四边形各边中点所组成的图形是矩形 D、平面内,经过平行四边形对角线交点的直线,一定能平分它的面积9. 超市经销一种水果,每千克盈利10元,每天销售500千克,经市场调查,若每千克涨价1元,则日销售量减少20千克,如果超市要保证每天盈利6000元,则每千克应该涨价( )A、15元或20元 B、10元或15元 C、10元或20元 D、5元或10元10. 如图,在矩形中,过点作对角线的垂线并延长,与的延长线交于点 , 与交于点 , 垂足为点 , 连接 , 且 , 则下列结论正确的有( )个:①;②;③;④
A、 B、 C、 D、8. 下面说法错误的是( )A、点 , 都在反比例函数图象上,且 , 则 B、若点是线段的黄金分割点, , , 则 C、顺次连接对角线互相垂直的四边形各边中点所组成的图形是矩形 D、平面内,经过平行四边形对角线交点的直线,一定能平分它的面积9. 超市经销一种水果,每千克盈利10元,每天销售500千克,经市场调查,若每千克涨价1元,则日销售量减少20千克,如果超市要保证每天盈利6000元,则每千克应该涨价( )A、15元或20元 B、10元或15元 C、10元或20元 D、5元或10元10. 如图,在矩形中,过点作对角线的垂线并延长,与的延长线交于点 , 与交于点 , 垂足为点 , 连接 , 且 , 则下列结论正确的有( )个:①;②;③;④ A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
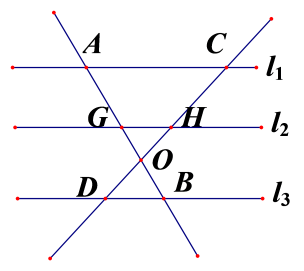
11. 若 , 则 .12. 若m,n是一元二次方程的两个实数根,则 .13. 如图,已知 , 则
 14. 如图,是一块锐角三角形余料,边 , 高 , 要把它加工成一个正方形零件,使一边在上,其余两个顶点分别在边、上.则该正方形的边长是m.
14. 如图,是一块锐角三角形余料,边 , 高 , 要把它加工成一个正方形零件,使一边在上,其余两个顶点分别在边、上.则该正方形的边长是m. 15. 如图,等腰中, , 点在上,且 , 连接 , 过点作于点 , 连接 , 则的值是 .
15. 如图,等腰中, , 点在上,且 , 连接 , 过点作于点 , 连接 , 则的值是 .
三、解答题
-
16. 解下列方程:(1)、;(2)、 .17. 为了解班级学生参加课后服务的学习效果,张老师对本班部分学生进行了为期一个月的追踪调查,他将调查结果分为四类:A:很好;:较好;:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
 (1)、此次调查的总人数为人;(2)、条形统计图缺少组女生和组男生的人数,请将它补充完整;(3)、该校九年级共有学生1000名,请你估计“达标”的共有人.(4)、为了共同进步,张老师准备从被调查的A类和类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.18. 如图,在正方形网格中,点、、都在格点上,利用格点按要求完成下列作图.(要求仅用无刻度的直尺,不要求写画法,保留必要的作图痕迹)
(1)、此次调查的总人数为人;(2)、条形统计图缺少组女生和组男生的人数,请将它补充完整;(3)、该校九年级共有学生1000名,请你估计“达标”的共有人.(4)、为了共同进步,张老师准备从被调查的A类和类学生中各随机抽取一位同学进行“一帮一”互助学习.请用画树状图或列表的方法求出所选两位同学恰好是相同性别的概率.18. 如图,在正方形网格中,点、、都在格点上,利用格点按要求完成下列作图.(要求仅用无刻度的直尺,不要求写画法,保留必要的作图痕迹) (1)、在图(1)中,以为位似中心,位似比为1:2,在格点上将放大得到;请画出(2)、在图(3)中,线段上作点 , 利用格点作图使得(3)、在图(2)中,利用格点在边上作一个点 , 使得 .19. 在中, , 是的中点,是的中点,过点作交的延长线于点 , 连接 .
(1)、在图(1)中,以为位似中心,位似比为1:2,在格点上将放大得到;请画出(2)、在图(3)中,线段上作点 , 利用格点作图使得(3)、在图(2)中,利用格点在边上作一个点 , 使得 .19. 在中, , 是的中点,是的中点,过点作交的延长线于点 , 连接 . (1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.20. 如图:为等腰直角三角形,斜边在轴上, , 一次函数的图象经过点A交轴于点 , 反比例函数的图象也经过点A.
(1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.20. 如图:为等腰直角三角形,斜边在轴上, , 一次函数的图象经过点A交轴于点 , 反比例函数的图象也经过点A. (1)、求反比例函数的解析式:(2)、若 , 求的面积;(3)、当时对应的自变量的取值范围是(请直接写出答案)21. 【综合与实践】:阅读材料,并解决以下问题.
(1)、求反比例函数的解析式:(2)、若 , 求的面积;(3)、当时对应的自变量的取值范围是(请直接写出答案)21. 【综合与实践】:阅读材料,并解决以下问题.【学习研究】:北师大版教材九年级上册第39页介绍了我国数学家赵爽在其所著的《勾股圆方图注》中关于一元二次方程的几何解法:以为例,构造方法如下:
首先将方程变形为 , 然后画四个长为 , 宽为的矩形,按如图(1)所示的方式拼成一个“空心”大正方形,则图中大正方形的面积可表示为 , 还可表示为四个矩形与一个边长为2的小正方形面积之和,即 , 因此,可得新方程: , 表示边长, , 即 , 遗憾的是,这样的做法只能得到方程的其中一个正根.

【类比迁移】:小明根据赵爽的办法解方程 , 请你帮忙画出相应的图形,将其解答过程补充完整:
第一步:将原方程变形为 , 即( ▲ )=4;
第二步:利用四个面积可用表示为 ▲ 的全等矩形构造“空心”大正方形(请在画图区画出示意图,标明各边长),并写出完整的解答过程;
第三步:
【拓展应用】:一般地对于形如:一元二次方程可以构造图2来解,已知图2是由4个面积为3的相同矩形构成,中间围成的正方形面积为4.那么此方程的系数 ▲ , ▲ , 求得方程的一个正根为 ▲ .
22. 如图1,直线与坐标轴的正半轴分别交于 , 两点,与反比例函数的图象交于 , 两点(点在点的左边),过点作轴于点 , 过点作轴于点 , 与交于点 . (1)、当点恰好是中点时,求此时点的横坐标;(2)、如图2,连接 , 求证:;(3)、如图3,将沿折叠,点恰好落在边上的点处,求此时反比例函数的解析式.
(1)、当点恰好是中点时,求此时点的横坐标;(2)、如图2,连接 , 求证:;(3)、如图3,将沿折叠,点恰好落在边上的点处,求此时反比例函数的解析式.