广东省深圳市龙岗区2022-2023学年九年级上学期期末考试数学试卷
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 下列四个几何体中,左视图为圆的是( )A、
 B、
B、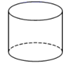 C、
C、 D、
D、 2. 如图,在矩形中,已知于 , , , 则的长为( )
2. 如图,在矩形中,已知于 , , , 则的长为( ) A、3 B、2 C、 D、3. 如图,在中,已知 , , , 则的值是( )
A、3 B、2 C、 D、3. 如图,在中,已知 , , , 则的值是( ) A、 B、 C、 D、4. 如图,已知直线l1l2l3 , 直线AC分别与直线l1 , l2 , l3 , 交于A、B、C三点,直线DF分别与直线l1 , l2 , l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1.则OF的长是( )
A、 B、 C、 D、4. 如图,已知直线l1l2l3 , 直线AC分别与直线l1 , l2 , l3 , 交于A、B、C三点,直线DF分别与直线l1 , l2 , l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1.则OF的长是( ) A、1 B、2 C、3 D、45. 一元二次方程的根的情况为( )A、无实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、不能判定6. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
A、1 B、2 C、3 D、45. 一元二次方程的根的情况为( )A、无实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、不能判定6. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 B、抛一个质地均匀的正六面体骰子,向上的面点数是5 C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” D、抛一枚硬币,出现反面的概率7. 如图,在平面直角坐标系中,已知 , , 与位似,原点O是位似中心.若 , 则点F的坐标是( ) A、 B、 C、 D、8. 如图,把一块长为 , 宽为的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为 , 设剪去小正方形的边长为 , 则所列方程正确的为( )
A、 B、 C、 D、8. 如图,把一块长为 , 宽为的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为 , 设剪去小正方形的边长为 , 则所列方程正确的为( ) A、 B、 C、 D、9. 已知二次函数 , 则该函数的图象可能为( )A、
A、 B、 C、 D、9. 已知二次函数 , 则该函数的图象可能为( )A、 B、
B、 C、
C、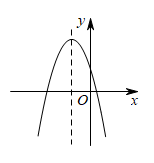 D、
D、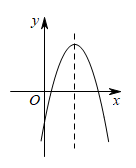 10. 如图,在菱形中,过点分别作边上的高 , 连接交于点 , 若点是的中点,则( )
10. 如图,在菱形中,过点分别作边上的高 , 连接交于点 , 若点是的中点,则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 ,则 的值为 .12. 计算:tan 45°+ cos 45°=13. 若是方程的两根,则的值为 .14. 如图,是反比例函数图象上一点,是反比例函数图象上一点,连接交轴于点 , 若 , , 则 .
 15. 如图,在正方形中, , E是的中点,F是边上一点,将沿折叠得到 , 连接并延长分别交 , 于O,H两点,若G是的中点,则 .
15. 如图,在正方形中, , E是的中点,F是边上一点,将沿折叠得到 , 连接并延长分别交 , 于O,H两点,若G是的中点,则 .
三、解答题
-
16. 解方程:.17. 某医院计划选派护士支援某地的防疫工作,甲、乙、丙、丁4名护士积极报名参加,其中甲是共青团员,其余3人均是共产党员.医院决定用随机抽取的方式确定人选.(1)、随机抽取1人,甲恰好被抽中的概率是;(2)、若需从这4名护士中随机抽取2人,请用画树状图法或列表法求出被抽到的两名护士都是共产党员的概率.18. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物的影长为16米,的影长为20米,小明的影长为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且 , . 已知小明的身高为1.8米.
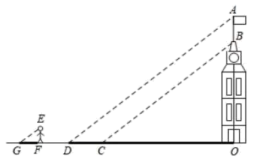 (1)、求建筑物OB的高度;(2)、求旗杆的高AB.19. 如图,在四边形中, , , 平分 , 连接交于点 , 过点作交延长线于点 .
(1)、求建筑物OB的高度;(2)、求旗杆的高AB.19. 如图,在四边形中, , , 平分 , 连接交于点 , 过点作交延长线于点 .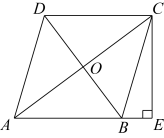 (1)、求证:四边形为菱形;(2)、若 , , 求的长.20. 某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克.为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.(1)、直接写出工厂每天的利润元与每千克降价元之间的函数关系式(要求化为一般式);(2)、若工厂每天的利润要达到9750元,并让利于民,则降价应为多少元?(3)、当降价为多少元时,有最大利润,最大利润是多少?21. 杠杆原理在生活中被广泛应用(杠杆原理:阻力×阻力臂=动力×动力臂,如图1,即),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图2).制作方法如下:第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm),确定支点 , 并用细麻绳固定,在支点左侧10cm的处固定一个金属吊钩,作为秤钩;第二步:取一个质量为1kg的金属物体作为秤砣.(备注:秤钩与称砣绳长的重量忽略不计)
(1)、求证:四边形为菱形;(2)、若 , , 求的长.20. 某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克.为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.(1)、直接写出工厂每天的利润元与每千克降价元之间的函数关系式(要求化为一般式);(2)、若工厂每天的利润要达到9750元,并让利于民,则降价应为多少元?(3)、当降价为多少元时,有最大利润,最大利润是多少?21. 杠杆原理在生活中被广泛应用(杠杆原理:阻力×阻力臂=动力×动力臂,如图1,即),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图2).制作方法如下:第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm),确定支点 , 并用细麻绳固定,在支点左侧10cm的处固定一个金属吊钩,作为秤钩;第二步:取一个质量为1kg的金属物体作为秤砣.(备注:秤钩与称砣绳长的重量忽略不计) (1)、图2中,把重物挂在秤钩上,秤砣挂在支点右侧的处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,的长度随之变化.设重物的质量为 kg,的长为 cm.则关于的函数解析式是;若 , 则的取值范围是 .(2)、调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点右侧的处,使秤杆平衡,如图3.设重物的质量为kg,的长为 cm.完成下列问题:
(1)、图2中,把重物挂在秤钩上,秤砣挂在支点右侧的处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,的长度随之变化.设重物的质量为 kg,的长为 cm.则关于的函数解析式是;若 , 则的取值范围是 .(2)、调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点右侧的处,使秤杆平衡,如图3.设重物的质量为kg,的长为 cm.完成下列问题:①关于的函数解析式是 ▲ ;
②完成下表:
/kg
…
0.25
0.5
1
2
4
…
/cm
…
▲
▲
▲
▲
▲
…
③在直角坐标系中画出该函数的图象.
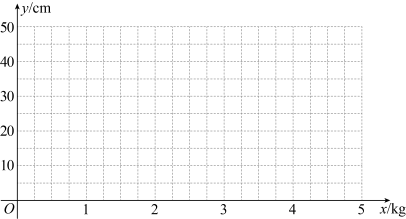 22. 如图
22. 如图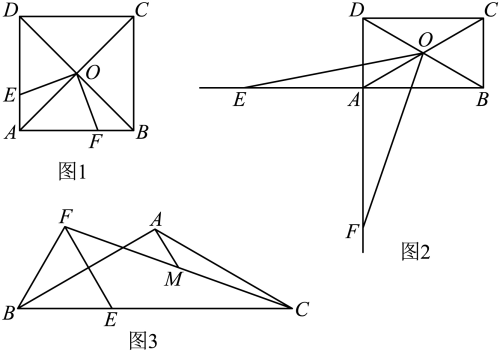 (1)、【探究发现】如图1,正方形的对角线交于点 , 是边上一点,作交于点 . 学习小队发现,不论点在边上运动过程中,与恒全等,请你证明这个结论;(2)、【类比迁移】如图2,矩形的对角线交于点 , , 是延长线上一点,将绕点逆时针旋转得到 , 点恰好落在的延长线上,求的值;(3)、【拓展提升】如图3,等腰中, , , , 点是边上一点,以为边在的上方作等边 , 连接 , 取的中点 , 连接 , 当时,直接写出的长.
(1)、【探究发现】如图1,正方形的对角线交于点 , 是边上一点,作交于点 . 学习小队发现,不论点在边上运动过程中,与恒全等,请你证明这个结论;(2)、【类比迁移】如图2,矩形的对角线交于点 , , 是延长线上一点,将绕点逆时针旋转得到 , 点恰好落在的延长线上,求的值;(3)、【拓展提升】如图3,等腰中, , , , 点是边上一点,以为边在的上方作等边 , 连接 , 取的中点 , 连接 , 当时,直接写出的长.