广东省广州市白云区2022-2023学年九年级上学期数学期末测试题
试卷更新日期:2023-01-05 类型:期末考试
一、单选题
-
1. 下列是一元二次方程的解是( )A、 B、 C、 , D、 ,2. 如图,弦于点E,过圆心O, , , 则( )
 A、4 B、8 C、 D、103. 已知抛物线与轴有两个不同的交点,则关于的一元二次方程根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定4. 下列图形中,不是中心对称图形的是( )A、圆 B、菱形 C、矩形 D、等边三角形5. 下列事件中,属于不可能事件的是( )A、某个数的绝对值小于0 B、某个数的相反数等于它本身 C、某两个数的和小于0 D、某两个负数的积大于06. 在同圆中,同弦所对的两个圆周角( )
A、4 B、8 C、 D、103. 已知抛物线与轴有两个不同的交点,则关于的一元二次方程根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定4. 下列图形中,不是中心对称图形的是( )A、圆 B、菱形 C、矩形 D、等边三角形5. 下列事件中,属于不可能事件的是( )A、某个数的绝对值小于0 B、某个数的相反数等于它本身 C、某两个数的和小于0 D、某两个负数的积大于06. 在同圆中,同弦所对的两个圆周角( )
A、相等 B、互补 C、相等或互补 D、互余7. 某厂今年一月份的总产量为500吨,三月份的总产量达到720吨,若平均每年的增长率是x,则可列方程()A、500(1+2x)=720 B、500(1+x)=720 C、500(1+x)=720 D、720(1+x)=5008. 下列说法中,正确的有( ).①相等的圆心角所对的弧相等;②平分弦的直径也平分弦所对的弧;③长度相等的两条弧是等弧;④经过圆心的每一条直线将圆分成两条等弧.
A、1个 B、2个 C、3个 D、4个9. 已知反比例函数 , 当时,y随x的增大而增大,那么一次函数的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限10. 圆心为O的两个同心圆,半径分别是2和3,若 , 则点P在( )A、大圆上 B、小圆内 C、大圆外 D、大圆内、小圆外二、填空题
-
11. 一元二次方程的根的判别式的值为 .12. 已知的半径 , 圆心O到直线l的距离 , 则直线l与的位置关系是 .13. 抛物线 的顶点坐标为 .14. 半径为3cm的圆内接正方形的对角线长为cm,面积为 .15. 点与关于原点对称,则A点坐标是 .16. 已知 ,且x,y是实数,则xy=.
三、解答题
-
17. 解关于x的方程:18. 已知,二次函数的图象如图所示,且该图象经过点 .
 (1)、c0(填“”、“”或“”);(2)、直接写出时,自变量x的取值范围;19. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球.(1)、用画树状图法求两次摸出的小球的标号不相同的概率;(2)、两次摸出的小球标号之和等于6的概率为 .20. 如图,中, , , 将绕点O顺时针旋转得到 , 边与交于点E,点D,B是对应点.
(1)、c0(填“”、“”或“”);(2)、直接写出时,自变量x的取值范围;19. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球.(1)、用画树状图法求两次摸出的小球的标号不相同的概率;(2)、两次摸出的小球标号之和等于6的概率为 .20. 如图,中, , , 将绕点O顺时针旋转得到 , 边与交于点E,点D,B是对应点. (1)、°.(2)、线段的长一定等于线段的长;(3)、求的度数.21. 如图,是的直径,点D在的延长线上,C为上的一点, , .
(1)、°.(2)、线段的长一定等于线段的长;(3)、求的度数.21. 如图,是的直径,点D在的延长线上,C为上的一点, , . (1)、求的度数;(2)、求证:是的切线.22. 某商住楼需要在楼顶平台建一个长方体储水池以便进行二次供水,水池的底面为正方形.由设计单位核算知,水池的总储水量为 . 若水池底面为S,高为h.
(1)、求的度数;(2)、求证:是的切线.22. 某商住楼需要在楼顶平台建一个长方体储水池以便进行二次供水,水池的底面为正方形.由设计单位核算知,水池的总储水量为 . 若水池底面为S,高为h. (1)、求出S与h的函数关系,并在所给的平面直角坐标系中画出函数的大致图象;(2)、若底面S为 , 则水池高度为多少m?(3)、楼顶平台长为30m,宽为15m,规定水池底面边长不超过楼顶平台宽的40%,同时考虑到楼顶平台承受能力,水池底面不能小于 , 则水池高度h在什么范围?23. 如图1,是的直径,过点B作的切线 , 弦 , 交于点F,且 , 连接、 , 延长交于点E.
(1)、求出S与h的函数关系,并在所给的平面直角坐标系中画出函数的大致图象;(2)、若底面S为 , 则水池高度为多少m?(3)、楼顶平台长为30m,宽为15m,规定水池底面边长不超过楼顶平台宽的40%,同时考虑到楼顶平台承受能力,水池底面不能小于 , 则水池高度h在什么范围?23. 如图1,是的直径,过点B作的切线 , 弦 , 交于点F,且 , 连接、 , 延长交于点E.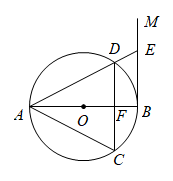 (1)、求证:是等边三角形;(2)、连接 , 若 , 求的长.
(1)、求证:是等边三角形;(2)、连接 , 若 , 求的长.

