重庆市潼南区六校联考2022-2023学年九年级上学期期中数学试题

试卷更新日期：2023-01-05 类型：期中考试

进入出卷网下载

一、单选题

1. 5的相反数是（）

A、-5 B、 $- \frac{1}{5}$ C、 $\frac{1}{5}$ D、5

查看试题解析
2. 下列图形是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若抛物线y=x²-2x+m与x轴有交点，则m的取值范围是（）

A、m＞1 B、m≥1 C、m＜1 D、m≤1

查看试题解析
4. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{5}$ B、 ${(a^{3})}^{2} = a^{5}$ C、 ${(2 a b^{2})}^{3} = 6 a^{3} b^{6}$ D、 $3 a^{2} \div 4 a^{2} = \frac{3}{4} a$

查看试题解析
5. 估计 $\sqrt{3} \times (2 \sqrt{3} + \sqrt{5})$ 的值应在（）

A、10和11之间 B、9和10之间 C、8和9之间 D、7和8之间

查看试题解析
6. 下列命题为真命题的是（）

A、菱形的四个角相等 B、菱形的对角线相等 C、菱形的四条边互相垂直 D、菱形是轴对称图形

查看试题解析
7. 小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（）

A、 $200 {(1 + x)}^{2} = 242$ B、 $200 {(1 - x)}^{2} = 242$ C、 $200 (1 + 2 x) = 242$ D、 $200 (1 - 2 x) = 242$

查看试题解析
8. 用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）

A、32 B、34 C、37 D、41

查看试题解析
9. 一次函数 $y_{1} = a x + b$ 与正比例函数 $y_{2} = - b x$ 在同一坐标系中的图象大致是（）

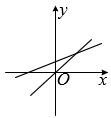A、 B、 C、 D、

查看试题解析
10. 如图，在正方形ABCD中，AE平分∠BAC交BC于点E，点F是边AB上一点，连接DF，若BE=AF，则∠CDF的度数为（）

A、45° B、60° C、67.5° D、77.5°

查看试题解析
11. 若关于x的一元一次不等式组 ${\begin{array}{l} x - 1 \geq \frac{4 x - 1}{3} \\ 5 x - 1 ＜ a \end{array}$ 的解集为 $x ≤ - 2$ ，且关于y的分式方程 $\frac{y - 1}{y + 1} = \frac{a}{y + 1} - 2$ 的解是负整数，则所有满足条件的整数a的值之和是（）

A、－26 B、－24 C、－15 D、－13

查看试题解析
12. 对多项式 $x - y - z - m - n$ 任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如： $(x - y) - (z - m - n) = x - y - z + m + n$ ， $x - y - (z - m) - n = x - y - z + m - n$ ， …，给出下列说法：
①至少存在一种“加算操作”，使其结果与原多项式相等；
②不存在任何“加算操作”，使其结果与原多项式之和为0；
③所有的“加算操作”共有8种不同的结果.
以上说法中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

13. 计算： $2^{- 2} + {(π - 1)}^{0} =$ .

查看试题解析
14. 已知点 $A (0 ， m)$ 、点 $B (3 ， n)$ 为抛物线 $y = a x^{2} - 2 a x + b$ 上一点，且 $a > 0$ ，则mn（填“>”或“<”）.

查看试题解析
15. 如图，直线 $y = x + 1$ 与 $y = m x + n$ 相交于点 $P (1 ， 2)$ ，则关于x，y的二元一次方程组 ${\begin{array}{l} y = x + 1 \\ y = m x + n \end{array}$ 的解为.

查看试题解析
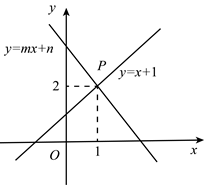16. 某新建商场设有百货部、服装部和家电部三个经营部，共有若干名售货员，平时全商场日营业额（指每日卖出商品所收到的总金额）为60万元，由于营业性质不同，分配到三个经营部的售货员的人数不等，所得利润也不同.根据经验，百货部、服装部、家电部各类商品每1万元营业额所需售货员人数依次为5人、4人、2人；所得利润占各自营业额的占比依次为 $\frac{3}{10}$ 、 $\frac{1}{2}$ 、 $\frac{1}{5}$ .临近妇女节人流量增加，商场决定将原百货部和家电部的售货员人数减少都调整到服装部，同时节日期间各类商品所得利润与各自营业额的占比依次变为 $\frac{2}{5}$ 、 $\frac{3}{5}$ 、 $\frac{3}{10}$ ，这样节日期间商场每日获得的利润比平时增加，且差价超过7万元，但不超过8万元.若百货部、服装部和家电部的营业额始终是整数，则节日期间从百货部调整到服装部的售货员共人.

查看试题解析

三、解答题

17. 解方程：

(1)、 $(x + 2)^{2} - 9 = 0$ ；

(2)、 $x^{2} + 6 x + 4 = 0$ .

查看试题解析
18. 如图， $A B$ // $C D$ ，点E是CD的中点.

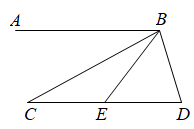(1)、用尺规完成以下基本作图：作∠BDC的平分线（保留作图痕迹，不写作法）；

(2)、在（1）的条件下，设∠BDC的平分线交AB于点F，连接EF交BC于点H，若HB＝HC，求证：四边形BDEF是菱形.
证明：∵点E是CD的中点，∴CE＝DE

∵CH＝BH，
∴    ，

∵ $A B$ // $C D$ ，
∴四边形BDEF是平行四边形

∵ $A B$ // $C D$ ，
∴

∵DF平分∠BDC，
∴   ∴∠BFD＝∠BDF，
∴    ，
∴四边形BDEF是菱形.

查看试题解析
19. 某中学利用班会课对全校学生进行了一次防疫知识测试活动，现从初二、初三两个年级各随机抽取了15名学生的测试成绩，得分用x表示（采取百分制，x为整数），共分成4组：A：60≤x＜70，B：70≤x＜80，C：80≤x＜90，D：90≤x≤100，对得分进行整理分析，给出了下面部分信息：
初二的测试成绩在C组中的数据为：80，86，88.
初三的测试成绩：76，83，100，88，81，100，82，71，95，90，100，93，89，86，86.
年级
平均数
中位数
最高分
众数
初二
88
a
98
98
初三
88
88
100
b

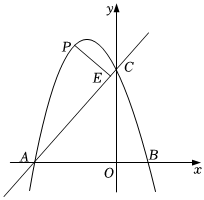
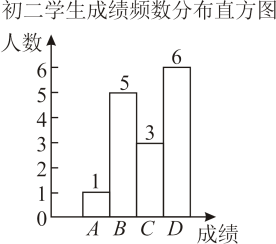(1)、a＝， b＝；

(2)、通过以上数据分析，你认为哪个年级学生对防疫知识的掌握更好？请写出一条理由；

(3)、若初二、初三共有3000名学生，请估计此次测试成绩达到90分及以上的学生约有多少人？

查看试题解析
20. 如图，直线 $A B$ 与x轴、y轴分别交于 $A (- 1 ， 0)$ 、B两点，与直线 $C D$ ： $y = - 3 x + 12$ 交于点D，且 $△ A C D$ 的面积为15.

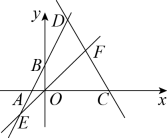(1)、求直线 $A B$ 的解析式；

(2)、直线 $E F$ 经过原点，与直线 $A B$ 交于点E，与直线 $C D$ 交于点F，若E点的横坐标为 $- 2$ ，求四边形 $O B D F$ 的面积.

查看试题解析
21. 小帆根据学习函数的过程与方法，对函数 $y = \frac{1}{4} x | a x + b |$ （ $a > 0$ ）的图象与性质进行探究.已知该函数图象经过点 $(2 ， 1)$ ，且与x轴的一个交点为 $(4 ， 0)$ .

(1)、求函数的解析式；

(2)、在给定的平面直角坐标系中：
①补全该函数的图象；
②当 $2 \leq x \leq 4$ 时，y随x的增大而      ▲      （在横线上填增大或减小）；
③当 $x < 4$ 时， $y = \frac{1}{4} x | a x + b |$ 的最大值是      ▲      ；
④直线 $y = k$ 与函数 $y = \frac{1}{4} x | a x + b |$ 有两个交点，则k=      ▲      .

查看试题解析
22. 冰墩墩和雪容融是北京奥运会和冬残奥会吉祥物，冰墩墩是一只熊猫，它的外表给人一种朴实的感觉，雪容融是一个灯笼，它的外表总能给人温暖.钥匙扣，手办两用冰墩墩和雪容融立体挂件在奥林匹克官方旗舰店销售异常火爆.

(1)、开售第一天，旗舰店共花费84000元从授权生产厂家购进两种挂件各1000件，其中1件雪容融挂件成本比1件冰墩墩挂件成本少6元，则1件雪容融挂件成本和1件冰墩墩挂件成本分别是多少元？

(2)、开售第一天，冰墩墩和雪容融挂件很快售罄，售价分别为65元和55元.第二天，旗舰店又以第一天的成本价从授权生产厂家购进一批两种挂件，其中冰墩墩挂件售价提高了0.05a元，销售比第一天减少了2a件，而雪容融挂件售价不变，销量比第一天增加了0.125a件，最终旗舰店第二天销售两种挂件共获利36000元，求a的值.

查看试题解析
23. 若一个四位正整数m满足前两个数字组成的两位数是后两个数字组成的两位数的2倍，则把这个四位数m称为“Double数”.
例如：2010的前两个数字组成的两位数是：20，后两个数字组成的两位数是：10，
∵ $20 = 2 \times 10$ ， ∴2010是“Double数”；
9246的前两个数字组成的两位数是：92，后两个数字组成的两位数是：46，
∵ $92 = 2 \times 46$ ， ∴9246是“Double数”；
7525的前两个数字组成的两位数是：75，后两个数字组成的两位数是：25，
∵ $75 \neq 2 \times 25$ ， ∴7525不是“Double数”.

(1)、判断7035，3814是否是“Double数”？并说明理由；

(2)、记一个“Double数”m各个数位数字之和为 $D (m)$ ，令 $G (m) = \frac{m - D (m)}{9}$ .当 $G (m)$ 能被8整除时，求出所有符合条件的“Double数”m.

查看试题解析
24. 抛物线 $y = a x^{2} + b x + 4$ 与x轴交于 $A (- 4 ， 0)$ 和 $B (1 ， 0)$ 两点，与y轴交于点C，点P是直线 $A C$ 上方的抛物线上一动点.

(1)、求抛物线的解析式；

(2)、过点P作 $P E ⊥ A C$ 于点E，求 $\frac{\sqrt{2}}{2} P E$ 的最大值及此时点P的坐标.

查看试题解析
25. $△ A B C$ 与 $△ D C E$ 均为等边三角形，D在边 $A C$ 上，连接 $B E$ .

(1)、如图 $1$ ，若 $A B = 4$ ， $C E = 2$ ，求 $B E$ 的长；

(2)、如图 $2$ ，若 $A B > D C$ ，在平面内将图 $1$ 中 $△ D C E$ 绕点C顺时针旋转 $α (0 ° < α < 120 °)$ ，连接 $B D$ 、 $A E$ ，交于点O，连接 $O C$ ，在 $△ C D E$ 运动过程中，猜想线段 $A O$ ， $O C$ ， $B O$ 之间存在的数量关系，并证明你的猜想.

查看试题解析

年级	平均数	中位数	最高分	众数
初二	88	a	98	98
初三	88	88	100	b