重庆市綦江区联盟校2022-2023学年九年级上学期期中数学试题
试卷更新日期:2023-01-05 类型:期中考试
一、单选题
-
1. 在下列方程中,属于一元二次方程的是( )A、x2-=2 B、ax2-bx+c=0 C、3x2-2xy+y2=0 D、(x-)2=02. 下列图形中,是中心对称图形的是( )A、
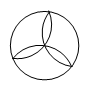 B、
B、 C、
C、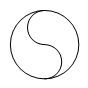 D、
D、 3. 一元二次方程根的情况是( )A、没有实数根 B、有两个不相等的实数根 C、无法判断 D、有两个相等的实数根4. 在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P的坐标是( )A、(3,1) B、(﹣3,﹣1) C、(﹣3,1) D、(﹣1,3)5. 已知函数的图像经过点(0,3),c的值是( )A、0 B、1 C、2 D、36. 抛物线的对称轴的方程是( )A、x=-1 B、x=1 C、 D、x=-27. 已知m是方程的一个根,则的值为( )A、4 B、 C、8 D、8. 抛物线过 , , 三点,则 , , 的大小关系是( )A、 B、 C、 D、9. 下列对抛物线性质的描写中,正确的是( )A、开口向上 B、对称轴是直线 C、顶点坐标是 D、函数y有最小值10. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( )
3. 一元二次方程根的情况是( )A、没有实数根 B、有两个不相等的实数根 C、无法判断 D、有两个相等的实数根4. 在平面直角坐标系中,点P(3,﹣1)关于坐标原点中心对称的点P的坐标是( )A、(3,1) B、(﹣3,﹣1) C、(﹣3,1) D、(﹣1,3)5. 已知函数的图像经过点(0,3),c的值是( )A、0 B、1 C、2 D、36. 抛物线的对称轴的方程是( )A、x=-1 B、x=1 C、 D、x=-27. 已知m是方程的一个根,则的值为( )A、4 B、 C、8 D、8. 抛物线过 , , 三点,则 , , 的大小关系是( )A、 B、 C、 D、9. 下列对抛物线性质的描写中,正确的是( )A、开口向上 B、对称轴是直线 C、顶点坐标是 D、函数y有最小值10. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( ) A、 B、 C、 D、11. 如图,函数和(a是常数,且)在同一个平面直角坐标系中的图象可能是( )A、
A、 B、 C、 D、11. 如图,函数和(a是常数,且)在同一个平面直角坐标系中的图象可能是( )A、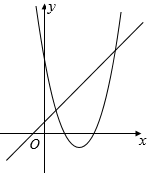 B、
B、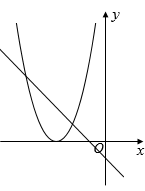 C、
C、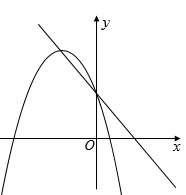 D、
D、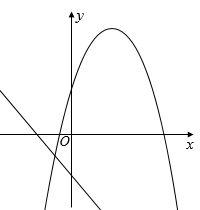 12. 对于一元二次方程 ,下列说法:
12. 对于一元二次方程 ,下列说法:①若 ,则 ;②若方程 有两个不相等的实根,则方程 必有两个不相等的实根;③若 是方程 的一个根,则一定有 成立;④若 是一元二次方程 的根,则 .
其中正确的有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
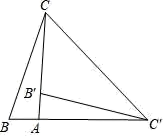
13. 的解是 .14. 若抛物线y=2x2+mx+8与x轴只有一个公共点,则m的值为 .15. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B= .
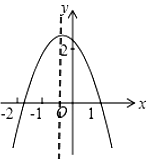
 16. 如图,二次函数 的图像与x轴交于和 , 且 , 与y轴的交点在上方,有以下结论:
16. 如图,二次函数 的图像与x轴交于和 , 且 , 与y轴的交点在上方,有以下结论:①;②;③;④;⑤当;其中正确的结论个数是.
三、解答题
-
17. 解一元二次方程(1)、;(2)、.18. 如图,在中, , , , 将绕点A按顺时针旋转一定角度得到 , 当点B的对应点D恰好落在BC边上时,求CD的长.
 19. 已知关于x的方程有两个实数根.(1)、求k的取值范围;(2)、当k取最大整数时,求此时方程的根.20. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .
19. 已知关于x的方程有两个实数根.(1)、求k的取值范围;(2)、当k取最大整数时,求此时方程的根.20. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .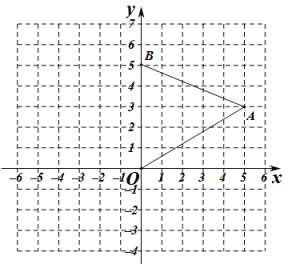 (1)、画出绕原点O逆时针方向旋转后得到的并写出 , 的坐标;(2)、在(1)的条件下,;21. 如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).
(1)、画出绕原点O逆时针方向旋转后得到的并写出 , 的坐标;(2)、在(1)的条件下,;21. 如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).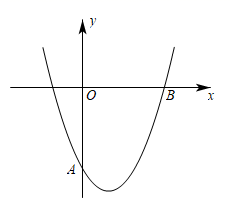 (1)、求b,c的值;(2)、连结AB,交抛物线L的对称轴于点M.求点M的坐标;22. 某水果超市经销一种高档水果,售价每千克50元.
(1)、求b,c的值;(2)、连结AB,交抛物线L的对称轴于点M.求点M的坐标;22. 某水果超市经销一种高档水果,售价每千克50元.(Ⅰ)若连续两次降价后每千克32元,且每次下降的百分率相同,求每次下降的百分率;
(Ⅱ)若按现售价销售,每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,超市决定采取适当的涨价措施,但超市规定每千克涨价不能超过8元,若每千克涨价1元,日销售量将减少20千克.现该超市希望每天盈利6000元,那么每千克应涨价多少元?
(Ⅲ)在(Ⅱ)的基础上,利用函数关系式求出每千克水果涨价多少元时,超市每天可获得最大利润?最大利润是多少?23. 材料:对任意一个n位正整数M ,若M与它的十位数字的p倍的差能被整数q整除,则称这个数为“p阶q级数”,例如:712是“5阶7级数”,因为=101;712也是“12阶10级数”,因为=70.(1)、若415是“5阶k级数”,且 , 求k的最大值;(2)、若一个四位数M的百位数字比个位数字大2,十位数字为1,且M既是“4阶13级数”又是“6阶5级数”,求这个四位数M.24. 已知抛物线的图象与x轴相交于点A和点 , 与y轴交于点C,连接 , 有一动点D在线段上运动,过点D作x轴的垂线,交抛物线于点E,交x轴于点F, , 设点D的横坐标为m.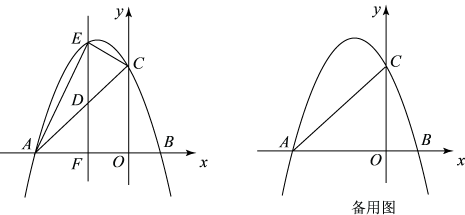 (1)、求抛物线的解析式;(2)、连接 , 当的面积最大时,求出的最大面积和点D的坐标;(3)、当时,在平面内是否存在点Q,使以B,C,E,Q为顶点的四边形为平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.25. 阅读下面材料,并解决问题:
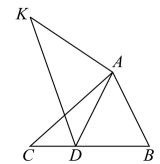
(1)、求抛物线的解析式;(2)、连接 , 当的面积最大时,求出的最大面积和点D的坐标;(3)、当时,在平面内是否存在点Q,使以B,C,E,Q为顶点的四边形为平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.25. 阅读下面材料,并解决问题: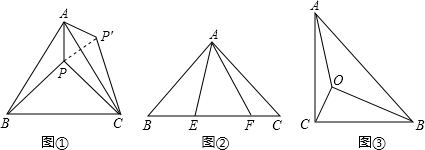 (1)、如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
(1)、如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=;
(2)、基本运用请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)、能力提升如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.