重庆市綦江区联盟校2022-2023学年八年级上学期期中数学试题

试卷更新日期：2023-01-05 类型：期中考试

进入出卷网下载

一、单选题

1. 用数学的眼光观察下面的网络图案，其中可以抽象成中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列四个图形中，线段AD是△ABC中BC边上的高的是（）

A、 B、 C、 D、

查看试题解析
3. 下列长度的各组线段可以组成三角形的是（）

A、2，3，5 B、5，7，4 C、4，4，8 D、2，4，6

查看试题解析
4. 如图所示，一扇窗户打开后，用窗钩 $A B$ 即可固定，这里所用的数学道理是（）

A、两定确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短

查看试题解析
5. 点 $A (- 4, 5)$ 关于x轴的对称点的坐标为（）

A、 $(4, - 5)$ B、 $(4, 5)$ C、 $(- 4, - 5)$ D、 $(- 4, 5)$

查看试题解析
6. 如图，已知 $A C = A D$ ，再添加一个条件仍不能判定 $Δ A B C ≅ Δ A B D$ 的是（）

A、 $∠ C = ∠ D = 90 °$ B、 $∠ B A C = ∠ B A D$ C、 $B C = B D$ D、 $∠ A B C = ∠ A B D$

查看试题解析
7. 如图，在△ABC中，DE为线段AB的垂直平分线.若△ABC的周长为18，线段AE的长度为4，则△BCD的周长为（　　）

A、10 B、11 C、12 D、14

查看试题解析
8. 观察下列图形，图①中有7个空心点，图②冲有11个空心点，图③中有15个空心点，…，按此规律排列下去，第9个图形中有（）个空心点.

A、36 B、38 C、39 D、41

查看试题解析
9. 如图， $A D$ 是 $Δ A B C$ 的 $B C$ 边上的高， $A E$ 平分 $∠ B A C$ ，若 $∠ B = 48 °$ ， $∠ C = 68 °$ ，则 $∠ D A E$ 的度数是（）

A、 $10 °$ B、 $12 °$ C、 $14 °$ D、 $16 °$

查看试题解析
10. 如图，五边形ABCDE中，AB∥CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则∠1+∠2+∠3＝（　　）

A、90° B、180° C、120° D、270°

查看试题解析
11. 如图，在△ABC中，G是边BC上任意一点，D、E、F分别是AG、BD、CE的中点，S_△ABC＝48，则S_△DEF的值为（　　）

A、4.8 B、6 C、8 D、12

查看试题解析
12. 如图，在 $△ A B C$ 中， $A B = A C ， ∠ B = ∠ C = 45 °$ ， D、E是斜边 $B C$ 上两点，且 $∠ D A E = 45 °$ ，过点A作 $A F ⊥ A D$ ，垂足是A，过点C作 $C F ⊥ B C$ ，垂足是C.交 $A F$ 于点F，连接 $E F$ ，下列结论：① $△ A B D ≌ △ A C F$ ；② $D E = E F$ ；③若 $S_{△ A D E} = 10 ， S_{△ C E F} = 4$ ，则 $S_{△ A B C} = 24$ ；④ $B D + C E = D E$ .其中正确个数是（）.

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 七边形的内角和是

查看试题解析
14. 小明从镜子中看到电子钟显示的时间是20：51，那么实际时间为 .

查看试题解析
15. 如图所示， $A C$ 平分 $∠ B A D ， ∠ B + ∠ D = 180 ° ， C E ⊥ A D$ 于点E， $A E = 10 c m ， A B = 8 c m$ ，那么 $D E$ 的长度为 $c m$ .

查看试题解析
16. 如图，CA⊥BC，垂足为C，AC=2cm，BC=6cm，射线BM⊥BQ，垂足为B，动点P从C点出发以1cm/s的速度沿射线CQ运动，点N为射线BM上一动点，满足PN=AB，随着P点运动而运动，当点P运动秒时，△BCA与点P、N、B为顶点的三角形全等.

查看试题解析

三、解答题

17. 若一个多边形的内角和的 $\frac{1}{4}$ 比它的外角和多 $90 °$ ，那么这个多边形的边数是多少？

查看试题解析
18. 如图， $A C$ 平分 $∠ B A D$ ， $A B = A D$ .求证： $B C = D C$ .

查看试题解析
19. 如图，在 $△ A B C$ 中， $∠ B A C = 70 °$ ， $∠ A C B = 50 °$ ， $∠ A C B$ 的平分线交 $A B$ 于点D.

(1)、尺规作图：作 $∠ A B C$ 的平分线 $B O$ 交 $C D$ 于点O.（保留作图痕迹，不写作法）

(2)、求 $∠ B O D$ 的度数.完成下列填空：
解∶（2）∵ $∠ B A C = 70 °$ ， $∠ A C B = 50 °$ ，

∴ $∠ A B C = 180 ° - 70 ° -___=___$ ，

∵ $C D$ 平分 $∠ A C B$ ， $B O$ 平分 $∠ A B C$ ，

∴ $∠ O C B = \frac{1}{2} ∠ A C B =____$ ， $∠ O B C = \frac{1}{2}____= 30 °$ ，

∴ $∠ B O D = ∠ O C B +____=____$

查看试题解析
20. 如图，已知A(-2，3)，B(-3，1)，C(1，-2).

(1)、请画出 $△$ ABC关于y轴对称的 $△ A^{'} B^{'} C^{'}$ ；（其中 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ 分别是A，B，C的对应点，不写画法）

(2)、 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ 的坐标分别为；

(3)、 $△$ ABC的面积是.

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ， D是 $A B$ 边的中点，E是 $A C$ 边上一点，过点B作 $B F ∥ A C$ ，交 $E D$ 的延长线于点F，若 $A D = 6$ ， $B F = 9$ ，求 $C E$ 的长.

查看试题解析
22. 已知在 $△ A B C$ 中，∠CAB的平分线AD与BC的垂直平分线DE交于点D， DM丄AB与M， DN丄AC交AC的延长线于N，你认为BM与CN之间有什么关系？试证明你的发现.

查看试题解析
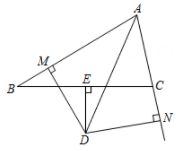23. 一个三位数a，各数位上数字不全相等且均不为0，将a的个位数字与前两位数字交换位置得到一个新的三位数为a'.记G（a）＝ $\frac{| a - a^{^{'}} |}{9}$ ，若G（a）能被8整除，则称该三位数a为“8仙数”.
例如：三位数493，∵G（493）＝ $\frac{1493 - 3491}{9}$ ＝16，16能被8整除，∴493是“8仙数”；

又如：三位数936，∵G（936）＝ $\frac{1936 - 693 |}{9}$ ＝27，27不能被8整除，∴936不是“8仙数”.

(1)、判断635，541是不是“8仙数”？并说明理由；

(2)、若一个三位数a是“8仙数”，且个位数字等于百位数字与十位数字之和，求满足条件的所有三位数a.

查看试题解析
24. 如图，等腰直角 $△ A B C$ 中， $C A = C B$ ， $∠ A C B = 90 °$ ， $∠ C A B = ∠ C B A = 45 °$ .点D在 $B A$ 的延长线上，连接 $C D$ ；过点C作 $C E ⊥ C D$ ，使 $C E = C D$ ，连接 $B E$ ，

(1)、求证： $A B ⊥ B E$ .

(2)、如图，若点N为 $B D$ 的中点，连接 $C N$ 、 $A E$ ；求证： $A E = 2 C N$ .

查看试题解析
25. 某学习小组在探究三角形全等时，发现了下面这种典型的基本图形，如下图1.

(1)、已知：在 $△ A B C$ 中，∠BAC＝90°，AB＝AC，直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点D、E.则线段DE与BD、CE的数量关系为.

(2)、组员小刘想，如果三个角不是直角，那（1）中的结论是否会成立呢？如图（2），将（1）中的条件改为：在 $△ A B C$ 中，AB＝AC，D、A、E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝ $α$ ，其中 $α$ 为任意锐角或钝角.如果（1）中的结论成立，请证明；如不成立，请说明理由.

(3)、数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图（3），过 $△ A B C$ 的边AB、AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I，求证：I是EG的中点

查看试题解析