重庆市开州区2022-2023学年九年级上学期期中数学试题

试卷更新日期：2023-01-05 类型：期中考试

进入出卷网下载

一、单选题

1. 2的相反数是（）

A、2 B、－2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列标志图中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 抛物线 $y = - 2 x^{2} + 4 x + 1$ 的对称轴是（）

A、直线 $x = 2$ B、直线 $x = - 2$ C、直线 $x = 1$ D、直线 $x = - 1$

查看试题解析
4. 估算 $\sqrt{12}$ 的值在(　　)

A、1与2之间 B、2与3之间 C、3与4之间 D、5与6之间

查看试题解析
5. 下列命题中，真命题是（）

A、对角线互相垂直的四边形是菱形 B、对角线互相垂直平分的四边形是正方形 C、四条边相等的四边形是矩形 D、有一组对边平行且相等的四边形是平行四边形

查看试题解析
6. 小明早晨从家骑车到学校，先上坡后下坡，行程情况如图所示.若返回时上坡、下坡的速度仍保持不变，那么小明从学校骑车回家用的时间是（）

A、30分钟 B、37.5分钟 C、43.5分钟 D、45分钟

查看试题解析
7. 已知一元二次方程x²－3x＋m＝0的一个解为2，则m的值为（）

A、1 B、－1 C、2 D、－2

查看试题解析
8. 1.如图，在△ABC中，点D、E分别是BC、AB上的中点，连接AD、DE，若S_△DEA＝3，则四边形AEDC的面积为（　　）

A、3 B、6 C、9 D、12

查看试题解析
9. 如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（）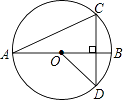

A、160° B、150° C、140° D、120°

查看试题解析
10. 函数 $y = x {}^{2}+ b x + c$ 与 $y = x$ 的图象如图所示，有以下结论：① $b^{2} - 4 c > 0$ ② $b + c = - 1$ ③ $3 b + c + 6 = 0$ ④当 $1 < x < 3$ 时， $x^{2} + (b - 1) x + c < 0$ .其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
11. 使得关于x的不等式组 ${\begin{array}{l} 6 x - a \geq - 10 \\ - 1 + \frac{1}{2} x < - \frac{1}{8} x + \frac{3}{2} \end{array}$ 有且只有4个整数解，且关于x的一元二次方程 $(a - 5) x^{2} + 4 x + 1 = 0$ 有实数根的所有整数a的值之和为（）

A、35 B、30 C、26 D、21

查看试题解析
12. 有n个依次排列的整式：第1项是 $a_{1} = x^{2} - x$ ，用第1项 $a_{1}$ 加上 $(x - 1)$ 得到 $b_{1}$ ，将 $b_{1}$ 乘以x得到第2项 $a_{2}$ ，再将第2项 $a_{2}$ 加上 $(x - 1)$ 得到 $b_{2}$ ，将 $b_{2}$ 乘以x得到第3项 $a_{3}$ ， …，以此类推，下面四个结论中正确的个数为（）
①方程 $a_{4} = 0$ 的实数解为 $\pm 1$ ；② $b_{9} = (x - 1) (x^{9} + x^{8} + x^{7} + ⋯ + x + 1)$ ；③第2023项 $a_{2023} = x^{2024} - x$ ；④当 $x = - 3$ 时，则 $\frac{b_{k}}{x - 1} (x \neq 1)$ 的值为 $\frac{1 - {(- 3)}^{k + 1}}{4}$ .

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 计算： $- 2^{2} + (3.14 - π)^{0} =$ .

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ B A C = 50 °$ ，将 $△ A B C$ 将绕点 $A$ 逆时针旋转70°得到 $△ A B^{'} C^{'}$ ，连接 $B B^{'}$ 、 $B C^{'}$ ，若 $A C^{'} = B C^{'}$ ，则 $∠ B^{^{'}} B C^{^{'}}$ 的度数为．

查看试题解析
15. 如图所示，点A与点B是两个四分之一圆的圆心，且两个圆的半径分别为3和6，则图中阴影部分的面积是.

查看试题解析
16. 某小区为了优化环境，计划在小区内甲、乙两块面积相同的空地上种植矮牵牛、金盏菊和三色堇三种花卉.现有10名工人参与种植，且每名工人每天种植矮牵牛、金盏菊和三色堇的面积之比为 $5 ： 4 ： 2$ .已知每名工人固定种植一种花卉，所有工人花费9天的时间完成了甲地的花卉种植.在乙地进行花卉种植时，为了加快乙地的种植进度，基于甲地的工人分配方案进行了调整，从种植金盏菊和三色堇的工人中分别抽调1人种植矮牵牛，这样乙地花卉种植的天数比甲地少且恰好为整数，则乙地种植金盏菊和三色堇的工人人数之比为.

查看试题解析

三、解答题

17. 解下列方程：

(1)、 $x^{2} - 8 x - 18 = 0$ ；

(2)、 $2 x^{2} + 6 x = x + 3$ .

查看试题解析
18. 如图，在四边形ABCD中，AD $∥$ BC且AD = $\frac{1}{2}$ BC，连接BD.

(1)、用尺规完成以下基本作图：作∠CDE，使∠CDE=∠C，DE与BC交于点F.（保留作图痕迹，不写作法，不下结论）

(2)、若∠BDC = 90°，求证：四边形ABFD为菱形.
证明：∵∠C=∠CDE
∴    ①
∵∠BDC = 90°
∴∠BDF +∠CDF = 90°，∠C +∠DBF = 90°
又∠C=∠CDE
∴    ②
∴BF = DF
∴BF=CF= $\frac{1}{2}$ BC
∵AD = $\frac{1}{2}$ BC，
∴     ③
∵AD $∥$ BC
∴四边形ABFD是平行四边形
∵    ④
∴四边形ABFD是菱形

查看试题解析
19. 化简下列各式：

(1)、（x﹣y）（3x﹣y）﹣（x﹣2y）²

(2)、 $\frac{x^{2} - 8 x + 16}{x^{2} + 2 x} \div (\frac{12}{x + 2} - x + 2) + \frac{1}{x + 4}$ ．

查看试题解析
20. 某校为了了解八、九年级男生立定跳远情况，现从八、九年级男生中各随机抽取了20名学生进行了测试，这些学生的成绩记为x（厘米），对数据进行整理，将所得的数据分为5组：（A组： $0 \leq x < 200$ ；B组： $200 \leq x < 220$ ；C组： $220 \leq x < 240$ ；D组： $240 \leq x < 250$ ；E组： $x \geq 250$ ）.学校对数据进行分析后，得到如下部分信息：
a.八年级被抽取的男生立定跳远成绩频数分布直方图
b.九年级被抽取的男生立定跳远成绩扇形统计图
c.八年级被抽取的男生的立定跳远成绩在 $220 \leq x < 240$ 这一组的数据是：
222 228 230 235 236 238
d.九年级被抽取的男生的立定跳远成绩在 $220 \leq x < 240$ 这一组的数据是：
228 235 238 238 238 238 238 239
e.八、九年级男生立定跳远成绩的平均数、中位数、众数如下：
年级
八年级
九年级
平均数
220
230
中位数
m
238
众数
218
k
根据以上信息，解答下列问题：

(1)、填空：m=；

(2)、若该校八年级有男生1400人、九年级有男生1600人，估计这两个年级男生立定跳远成绩不低于220的人数一共多少人；

(3)、根据以上数据分析，你认为该校八、九年级中哪个年级的男生立定跳远成绩更优异，请说明理由.（写出一条理由即可）

查看试题解析
21. 春节期间，某水果店购进了100千克水蜜桃和50千克苹果，苹果的进价是水蜜桃进价的1.2倍，水蜜桃以每千克16元的价格出售，苹果以每千克20元的价格出售，当天两种水果均全部停出，水果店获利1800元.

(1)、求水蜜桃的进价是每千克多少元?

(2)、第一批水蜜桃售完后，该水果店又以相同的进价购进了300千克水蜜桃，商家见第一批水果卖得很好，于是第一天将水蜜桃价格涨价到每千克17元的价格出售，售出了8a千克，由于水蜜桃不易保存，第二天，水果店将水蜜桃的价格在原先每千克16元的基础上还降低了0.1a元，到了晚上关店时，还剩20千克没有售出，店主便将剩余水蜜桃分发给了水果店员工们，结果这批水蜜桃的利润为2980元，求a的值.

查看试题解析
22. 已知一次函数 $y = k x + b (b \neq 0)$ 的图象与二次函数 $y = \frac{1}{2} {(x + 2)}^{2} - 2$ 的图象相交于点 $A (1 ， m) ， B (- 2 ， n)$ .

(1)、求一次函数的表达式，并在图中画出这个一次函数的图象；

(2)、根据函数图象，直接写出不等式 $k x + b < \frac{1}{2} {(x + 2)}^{2} - 2$ 的解集；

(3)、若点C是点B关于x轴的对称点，连接 $A C$ ， $B C$ ，求 $△ A B C$ 的面积.

查看试题解析
23. 对任意一个三位数n，如果其个位数上的数字与百位上的数字之和等于十位上的数字，则称n为“明亮数”.现将n的个位作为十位，十位作为百位，百位作为个位，得到一个新数 $n^{'}$ ，规定 $F (n) = \frac{n^{'} - n}{9}$ ，例如132是一个“明亮数”，将其个位作为十位，十位作为百位，百位作为个位，得到一个新数 $n^{'} = 321$ ，所以 $F (132) = \frac{321 - 132}{9} = 21$ .

(1)、当 $n = 473$ 时， $F (473) =$ ；

(2)、一个三位数，当其百位上的数字比个位上的数字少2时， $F (n) =$ ；

(3)、若 $F (n)$ 是8的倍数，则称这样的n为“幸运20明亮数”，求出所有的“幸运20明亮数”.

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + 3$ 交x轴于点 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ ，与y轴交于点C，连接 $B C$ .

(1)、求抛物线的解析式；

(2)、点P是直线 $B C$ 上方的抛物线上的一点，连接 $P B$ ， $P C$ ，求 $△ P B C$ 的面积的最大值以及此时点P的坐标；

(3)、将抛物线 $y = a x^{2} + b x + 3$ 向右平移1个单位得到新抛物线，点M是新抛物线的对称轴上的一点，N是新抛物线一动点，当以M、N、B、C为顶点的四边形是平行四边形，直接写出点M的坐标.

查看试题解析
25. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点D为 $B C$ 边上一动点，连接 $A D$ ，将 $A D$ 绕着D点逆时针方向旋转 $90 °$ 得到 $D E$ ，连接 $A E$ .

(1)、如图1， $A H ⊥ B C$ ，点D恰好为 $C H$ 中点， $A E$ 与 $B C$ 交于点G，若 $A B = 4$ ，求 $A E$ 的长度；

(2)、如图2， $D E$ 与 $A B$ 交于点F，连接 $B E$ ，在 $B A$ 延长线上有一点P， $∠ P C A = ∠ E A B$ ，求证： $A B = A P + \sqrt{2} B D$ ；

(3)、如图3， $D E$ 与 $A B$ 交于点F，且 $A B$ 平分 $∠ E A D$ ，点M为线段 $A F$ 上一点，点N为线段 $A D$ 上一点，连接 $D M$ ， $M N$ ，点K为 $D M$ 延长线上一点，将 $△ B D K$ 沿直线 $B K$ 翻折至 $△ B D K$ 所在平面内得到 $△ B Q K$ ，连接 $D Q$ ，在M，N运动过程中，当 $D M + M N$ 取得最小值，且 $∠ D K Q = 4 5^{°}$ 时，请直接写出 $\frac{D Q}{B C}$ 的值.

查看试题解析

年级	八年级	九年级
平均数	220	230
中位数	m	238
众数	218	k