重庆市丰都县十三校联考2022-2023学年七年级上学期期中数学试题

试卷更新日期：2023-01-05 类型：期中考试

进入出卷网下载

一、单选题

1. －2022的相反数是（）

A、2022 B、－2022 C、 $\frac{1}{2022}$ D、－ $\frac{1}{2022}$

查看试题解析
2. 下列运算正确的是（　　）

A、 $3 x^{2} - x^{2} = 2$ B、 $2 a + 3 a = 5 a^{2}$ C、 $2 a b - 2 a = b$ D、 $2 x^{2} y - 4 y x^{2} = - 2 x^{2} y$

查看试题解析
3. 4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点439 000米．将439 000用科学记数法表示应为（）

A、0.439×10⁶ B、4.39×10⁶ C、4.39×10⁵ D、139×10³

查看试题解析
4. 若 $| a | = - a$ ，则a的取值范围是（）

A、 $a$ ＞0 B、 $a$ ≥0 C、 $a$ ＜0 D、 $a$ ≤0

查看试题解析
5. 下列方程中，一元一次方程共有（）个
① $4 x - 3 = 5 x - 2$ ；② $3 x - 4 y = 5$ ；③ $3 x + 1 =$ $\frac{1}{x}$ ； ④ $\frac{3 x - 1}{4} +$ $\frac{1}{5}$ $= 0$ ；⑤ $x^{2} + 3 x + 1 = 0$ ；⑥ $x - 1 = 12$

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 若 $3 x^{m + 5} y^{2}$ 与 $x^{3} y^{n}$ 的和是单项式，则 $m^{n}$ 的值为（）

A、-4 B、4 C、 $- \frac{1}{4}$ D、 $\frac{1}{4}$

查看试题解析
7. 运用等式性质进行的变形，一定正确的是（）

A、如果 $a = b$ ，那么 $a + c = b - c$ B、如果 $a + c = b - c$ ，那么 $a = b$ C、如果 $a = b$ ，那么 $\frac{a}{c} = \frac{b}{c}$ D、如果 $\frac{a}{c} = \frac{b}{c}$ ，那么 $a = b$

查看试题解析
8. 多项式 $x^{2} - \frac{1}{2} k x y - 5 y^{2} + x y - 6$ 合并同类项后不含xy项，则k的值是（　　）

A、0 B、1 C、2 D、-2

查看试题解析
9. 下列说法：①符号相反的数互为相反数；②两个四次多项式的和一定是四次多项式；③若abc＞0，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或-1；④如果a大于b，那么a的倒数小于b的倒数；⑤若a³＋b³＝0，则a、b互为相反数.其中正确的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 已知a，b，c在数轴上的位置如图所示，则 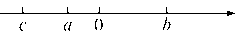$| a + b | + | a + c | - | b - c | =$ （）

A、0 B、 $2 a + 2 b$ C、 $2 b - 2 c$ D、 $2 a + 2 c$

查看试题解析
11. 已知|x|=5，|y|=2，且|x+y|=﹣x﹣y，则x﹣y的值为（）

A、±3 B、±3或±7 C、﹣3或7 D、﹣3或﹣7

查看试题解析
12. 如图所示，在这个数据运算程序中，若开始输入的x的值为2，结果输出的是1，返回进行第二次运算则输出的是﹣4，…，则第2020次输出的结果是（　　）

A、﹣1 B、3 C、6 D、8

查看试题解析

二、填空题

13. 写出一个只含有字母x，y，系数为-2的三次单项式.

查看试题解析
14. 若 $| a + 2 | + (b - 3)^{2} = 0$ ，则 $a^{b}$ 的值为.

查看试题解析
15. 已知x= - 1是关于x的方程 $2 x + a x + b = 0$ 的解，则代数式100-3a+3b=。

查看试题解析
16. 定义：a是不为1的有理数，我们把 $\frac{1}{1 - a}$ 称为a的差倒数，如：2的差倒数是 $\frac{1}{1 - 2}$ =－1，－1的差倒数是 $\frac{1}{1 - (- 1)}$ = $\frac{1}{2}$ .已知a₁=－ $\frac{1}{2}$ ， a₂是a₁的差倒数，a₃是a₂的差倒数，a₄是a₃的差倒数，以此类推，则a₂₀₁₆= .

查看试题解析

三、解答题

17. 把下列各数： $- (+ 4)$ ， $| - 3 |$ ， $0$ ， $- 1 \frac{2}{3}$ ， $1.5$

(1)、分别在数轴上表示出来：

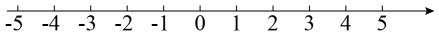(2)、将上述的有理数填入图中相应的圈内.

查看试题解析
18. 计算：

(1)、 $2 a - 5 b + 3 a + b$

(2)、 $3 (2 a^{2} b - a b^{2}) - 4 (a b^{2} - 3 a^{2} b)$

查看试题解析
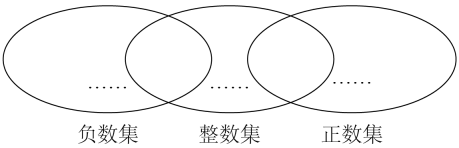19. 计算下列各题：

(1)、 $(1 - \frac{1}{6} + \frac{3}{4}) \times (- 24)$ ；

(2)、 $- 1^{4} - (- 1 + \frac{2}{3}) \times \frac{1}{2} \times [2 - (- 3)^{2}]$ .

查看试题解析
20. 化简求值： $2 x^{2} - y^{2} + \frac{1}{2} (4 y^{2} - 2 x^{2}) - 2 (x^{2} + \frac{3}{2} y^{2})$ ，其中x＝-2，y＝1.

查看试题解析

21. 现有15箱苹果，以每箱25kg为标准，超过或不足的部分分别用正、负数来表示，记录如下表，请解答下列问题：

标准质量的差（单位：kg）	$- 2$	$- 1.5$	$- 1$	0	2	$2.5$	3
箱数	1	3	2	2	2	4	1

(1)、15箱苹果中，最重的一箱比最轻的一箱重多少千克？

(2)、与标准质量相比，15箱苹果的总重量共计超过或不足多少千克？

(3)、若苹果每千克售价为8元，则这15箱苹果全部售出共可获利多少元？

查看试题解析

22. 已知 $A = 2 a^{2} b + a b c$ ，小红错将“ $2 A - B$ ”看成了“ $2 A + B$ ”，算得结果为 $5 a^{2} b + 4 a b c$ .

(1)、求B；

(2)、小军跟小红说：“ $2 A - B$ 的大小与c取值无关”，小军的说法对吗？为什么？

查看试题解析
23. 【概念学习】规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（-3）÷（-3）÷（-3）÷（-3）等.类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（-3）÷（-3）÷（-3）÷（-3）记作（-3）④，读作“-3的圈4次方”，一般地，把 $\underset{n 个 a}{\underset{︸}{a \div a \div a \div ⋯ \div a}}$ （a≠0）记作aⓝ，读作“a的圈n次方”.

(1)、【初步探究】直接写出计算结果：2③＝， $(- \frac{1}{2})$ ④＝；

(2)、关于除方，下列说法错误的是　　.

A、任何非零数的圈2次方都等于1； B、对于任何正整数n，1ⓝ＝1； C、3④＝4③； D、负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数.

(3)、
【深入思考】我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算有理数的除方运算如何转化为乘方运算呢？

想一想：将一个非零有理数a的圈n次方写成幂的形式等于；

(4)、算一算： $(- \frac{1}{3})$ ④× $(- \frac{1}{2})$ ③－ $(- \frac{1}{3})$ ⑧÷ $3^{6}$ .

查看试题解析
24. 在数的学习过程中，一些具有某种特性的数总能引起人们的注意，如学习自然数时，我们发现一种特殊的自然数--“美数”.定义，对于三位自然数n，各位数字都不为 $0$ ，且百位数字与个位数字之和被十位数字除后余 $2$ ，则称这个自然数n为“美数”.例如： $365$ 是“美数”，因为 $3 ， 6 ， 5$ 都不为 $0$ ，且 $3 + 5 = 8 ， 8$ 被 $6$ 除余 $2$ ； $158$ 不是“美数”，因为 $1 + 8 = 9 ， 9$ 被 $5$ 除余 $4$ .

(1)、判断：779“美数”，436“美数”(填“是”或“不是”)

(2)、400以内，个位数字比百位数字大 $5$ 的所有“美数”为 .

(3)、求出十位数字为 $5$ 且被 $3$ 整除的所有“美数”.

查看试题解析
25. 在学习了数轴后，小亮决定对数轴进行变化应用：

(1)、应用一：已知点A在数轴上表示为-2，数轴上任意一点B表示的数为x，则 $A B$ 两点的距离可以表示为；
应用这个知识，

①找出所有符合条件的整数x，使 $| x + 5 | + | x - 2 | = 7$ 成立.

②对于任何有理数x， $| x - 3 | + | x - 6 |$ 是否有最小值？请说明理由.

(2)、应用二：从数轴上取下一个单位长度的线段，第一次剪掉原长的 $\frac{1}{2}$ ，第二次剪掉剩下的 $\frac{1}{2}$ ，依此类推，每次都剪掉剩下的 $\frac{1}{2}$ ，则剪掉 $5$ 次后剩下线段的长度为；应用这个原理，请计算： $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ⋯ + \frac{1}{2^{n}} =$ .

查看试题解析