重庆市丰都县十三校联考2022-2023学年八年级上学期期中数学试题
试卷更新日期:2023-01-05 类型:期中考试
一、单选题
-
1. 以下四大通讯运营商的企业图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,将三角形纸片剪掉一角得四边形,设△ABC与四边形BCDE的外角和的度数分别为 , ,则正确的是( )
2. 如图,将三角形纸片剪掉一角得四边形,设△ABC与四边形BCDE的外角和的度数分别为 , ,则正确的是( ) A、 B、 C、 D、无法比较 与 的大小3. 下列各图中,作△ABC边AC上的高,正确的是( )A、
A、 B、 C、 D、无法比较 与 的大小3. 下列各图中,作△ABC边AC上的高,正确的是( )A、 B、
B、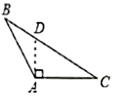 C、
C、 D、
D、 4. 如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是( )
4. 如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是( ) A、等边对等角 B、垂线段最短 C、等腰三角形“三线合一” D、线段垂直平分线上的点到这条线段两端点的距离相等5. 下列各组三条线段中,不是三角形三边长的是( )A、 , , B、 , , C、三条线段之比为 :: D、 , ,6. 如图, 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以 , 为圆心、以大于 的长为半径作弧,两弧在 内交于点 ;作射线 交 于点 .若 的面积为4, , 为 上一动点,则 的最小值为( )
A、等边对等角 B、垂线段最短 C、等腰三角形“三线合一” D、线段垂直平分线上的点到这条线段两端点的距离相等5. 下列各组三条线段中,不是三角形三边长的是( )A、 , , B、 , , C、三条线段之比为 :: D、 , ,6. 如图, 中, ,利用尺规在 , 上分别截取 , ,使 ;分别以 , 为圆心、以大于 的长为半径作弧,两弧在 内交于点 ;作射线 交 于点 .若 的面积为4, , 为 上一动点,则 的最小值为( )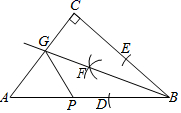 A、无法确定 B、4 C、3 D、27. 如图,在中,点D为边上一点,给出如下关系:①平分;②于D;③D为中点.甲说:如果①②同时成立,可证明;乙说:如果②③同时成立,可证明;丙说:如果①③同时成立,可证明.则正确的说法是( )
A、无法确定 B、4 C、3 D、27. 如图,在中,点D为边上一点,给出如下关系:①平分;②于D;③D为中点.甲说:如果①②同时成立,可证明;乙说:如果②③同时成立,可证明;丙说:如果①③同时成立,可证明.则正确的说法是( ) A、甲、乙正确,丙错误 B、甲正确,乙、丙错误 C、乙正确,甲、丙错误 D、甲、乙、丙都正确8. 如图,把沿线段折叠,使点B落在点F处;若 , , , 则的度数为( )
A、甲、乙正确,丙错误 B、甲正确,乙、丙错误 C、乙正确,甲、丙错误 D、甲、乙、丙都正确8. 如图,把沿线段折叠,使点B落在点F处;若 , , , 则的度数为( ) A、 B、 C、 D、9. 若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,∠BAD=90°,AC平分∠BAD,CB=CD,则∠B与∠ADC满足的数量关系为( )
A、 B、 C、 D、9. 若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,∠BAD=90°,AC平分∠BAD,CB=CD,则∠B与∠ADC满足的数量关系为( ) A、∠B=∠ADC B、2∠B=∠ADC C、∠B+∠ADC=180° D、∠B+∠ADC=90°11. 如图,在中, , 的平分线交于点E,于点D,若的周长为 , 则的周长为 , 则( )
A、∠B=∠ADC B、2∠B=∠ADC C、∠B+∠ADC=180° D、∠B+∠ADC=90°11. 如图,在中, , 的平分线交于点E,于点D,若的周长为 , 则的周长为 , 则( ) A、 B、 C、 D、12. 如图,已知等边和等边 , 点P在的延长线上,的延长线交于点M,连接;下列结论:①;②;③平分;④ , 其中正确的有( )
A、 B、 C、 D、12. 如图,已知等边和等边 , 点P在的延长线上,的延长线交于点M,连接;下列结论:①;②;③平分;④ , 其中正确的有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题
-
13. 如图是由一副三角板拼凑得到的.图中的∠ABC的度数为.
 14. 等腰三角形的底边长为 , 一腰上的中线把其周长分成两部分的差为 , 则腰长是.15. 如图,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为°.
14. 等腰三角形的底边长为 , 一腰上的中线把其周长分成两部分的差为 , 则腰长是.15. 如图,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为°. 16. 已知中, , 将、按照如图所示折叠,若 , 则.
16. 已知中, , 将、按照如图所示折叠,若 , 则.
三、解答题
-
17. 如图,在中,平分 , , 求:
 (1)、的度数;(2)、的度数.18. 如图,已知点B,E,C,F在同一直线上, , , 求证:≌.
(1)、的度数;(2)、的度数.18. 如图,已知点B,E,C,F在同一直线上, , , 求证:≌. 19. 如图,分别过点C、B作的边上的中线及其延长线的垂线,垂足分别为E、F.
19. 如图,分别过点C、B作的边上的中线及其延长线的垂线,垂足分别为E、F. (1)、求证:;(2)、若的面积为 , 的面积为 , 求的面积.20. 如图所示,在中,为边上的高.
(1)、求证:;(2)、若的面积为 , 的面积为 , 求的面积.20. 如图所示,在中,为边上的高. (1)、尺规作图:作出的垂直垂直平分线 , 交于点E,于点F(不写作法,保留作图痕迹)(2)、连接 , 若 , , 求的度数.21. 如图,在中, , , 点E是内部一点,连接 , 作 , , 垂足分别为点D,E.
(1)、尺规作图:作出的垂直垂直平分线 , 交于点E,于点F(不写作法,保留作图痕迹)(2)、连接 , 若 , , 求的度数.21. 如图,在中, , , 点E是内部一点,连接 , 作 , , 垂足分别为点D,E. (1)、证明:;(2)、若 , , 求的长.22. 在平面直角坐标系中,的位置如图所示,其中B点的坐标 , 先将先向左平移个单位,再向上平移两个单位长度,得到 , 与关于x轴对称.
(1)、证明:;(2)、若 , , 求的长.22. 在平面直角坐标系中,的位置如图所示,其中B点的坐标 , 先将先向左平移个单位,再向上平移两个单位长度,得到 , 与关于x轴对称.
( 1 )画出 , 并写出的坐标;
( 2 )求的面积;
( 3 )在x轴上画出点Q,使得的值最小,直接写出Q点坐标.23. 对于一个三位数,若其十位上的数字是5、各个数位上的数字互不相等且都不为0,则称这样的三位数为“可爱数”;如357就是一个“可爱数”.将“可爱数”m任意两个数位上的数字取出组成两位数,则一共可以得到6个两位数,将这6个两位数的和记为例如:
(1)、求的值;(2)、规定:与1的商记为 , 即.例如:.若“可爱数”n满足( , 且x,y均为整数),即n的百位上的数字是x、十位上的数字是5、个位上的数字是y,且 , 请求出所有满足条件的“可爱数”n.

