海南省海口市2022-2023学年九年级上学期期中数学试题
试卷更新日期:2023-01-05 类型:期中考试
一、单选题
-
1. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、2. 当x为下列何值时,二次根式 有意义( )A、 B、 C、 D、3. 已知 是整数,则满足条件的最小正整数n为( )A、2 B、3 C、4 D、54. 若 , .则代数式的值是( )A、 B、3 C、 D、5. 方程是关于x的一元二次方程,则m满足的条件是( ).A、 B、 C、 D、6. 用配方法解一元二次方程 , 配方正确的是( )A、 B、 C、 D、7. 已知的两个根为、 , 则的值为( )A、2 B、-2 C、3 D、-38. 在平面直角坐标系中,点 关于 轴对称的点的坐标为( )A、 B、 C、 D、9. 如图,某小区居民休闲娱乐中心是一块长方形(长30米,宽20米)场地,被3条宽度相等的绿化带分为总面积为480平方米的活动场所(羽毛球,乒乓球)如果设绿化带的宽度为x米,由题意可列方程为( )
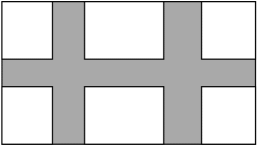 A、 B、 C、 D、10. 如图所示,每个小正方形的边长均为1,则下列四个图中的三角形(阴影部分)与相似的是( )
A、 B、 C、 D、10. 如图所示,每个小正方形的边长均为1,则下列四个图中的三角形(阴影部分)与相似的是( ) A、
A、 B、
B、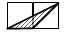 C、
C、 D、
D、 11. 如图,在平行四边形ABCD中,E为CD上一点,连接AE , BD , 且AE , BD交于点F , : :25,则DE: =( )
11. 如图,在平行四边形ABCD中,E为CD上一点,连接AE , BD , 且AE , BD交于点F , : :25,则DE: =( )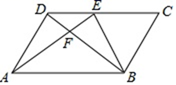 A、2:5 B、3:2 C、2:3 D、5:312. 如图,在中, , D,E分别是 , 的中点,F是上一点, , 连接 , , 若 , 则的长度为( )
A、2:5 B、3:2 C、2:3 D、5:312. 如图,在中, , D,E分别是 , 的中点,F是上一点, , 连接 , , 若 , 则的长度为( )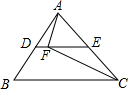 A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14二、填空题
-
13. 在数轴上表示实数a的点如图所示,化简 +|a-2|的结果为 .
 14. 将一元二次方程x2+8x+13=0通过配方转化成(x+n)2=p的形式(n,p为常数),则n= , p=.15. 如图,已知和的相似比是 , 且的面积是3,则四边形的面积是.
14. 将一元二次方程x2+8x+13=0通过配方转化成(x+n)2=p的形式(n,p为常数),则n= , p=.15. 如图,已知和的相似比是 , 且的面积是3,则四边形的面积是. 16. 如图,P为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .
16. 如图,P为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .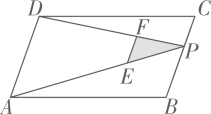
三、解答题
-
17. 计算:(1)、;(2)、.18. 解方程:(1)、;(2)、.19. “疫情”期间,某商场积压了一批商品,现欲尽快清仓,确定降价促销.据调查发现,若每件商品盈利50元时,可售出500件,商品单价每下降1元,则可多售出20件.设每件商品降价x元.(1)、每件商品降价x元后,可售出商品件(用含x的代数式表示).(2)、若要使销售该商品的总利润达到28000元,求x的值.(3)、销售该商品的总利润能否达到30000元?若能,请求出此时的单价;若不能,请说明理由.20. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .

( 1 )画出与关于y轴对称的;
( 2 )以原点O为位似中心,在第三象限内画一个 , 使它与的相似比为 , 并写出点 , , 的坐标.
( 3 )若方格中每个小正方形的边长为1个单位长度,求的面积.

