2023年中考数学精选真题实战测试11 一元一次方程与二元一次方程组A

试卷更新日期：2023-01-05 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列说法中，正确的是（）

A、若 $a c = b c$ ，则 $a = b$ B、若 $a^{2} = b^{2}$ ，则 $a = b$ C、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ D、若 $- \frac{1}{3} x = 6$ ，则 $x = 2$

查看试题解析
2. 植树节当天，七年级1班植树300棵，正好占这批树苗总数的 $\frac{3}{5}$ ，七年级2班植树棵数是这批树苗总数的 $\frac{1}{5}$ ，则七年级2班植树的棵数是（）

A、36 B、60 C、100 D、180

查看试题解析
3. 《孙子算经》是我国古代经典数学名著，其中有一道“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足.问鸡兔各几何？”学了方程（组）后，我们可以非常顺捷地解决这个问题，如果设鸡有 $x$ 只，兔有 $y$ 只，那么可列方程组为（）

A、 ${\begin{array}{l} x + y = 35 \\ 4 x + 4 y = 94 \end{array}$ B、 ${\begin{array}{l} x + y = 35 \\ 4 x + 2 y = 94 \end{array}$ C、 ${\begin{array}{l} x + y = 94 \\ 4 x + 4 y = 35 \end{array}$ D、 ${\begin{array}{l} x + y = 35 \\ 2 x + 4 y = 94 \end{array}$

查看试题解析
4. 对于二元一次方程组 ${\begin{array}{l} y = x - 1 ① \\ x + 2 y = 7 ② \end{array}$ ，将①式代入②式，消去 $y$ 可以得到（）

A、 $x + 2 x - 1 = 7$ B、 $x + 2 x - 2 = 7$ C、 $x + x - 1 = 7$ D、 $x + 2 x + 2 = 7$

查看试题解析
5. 我国“DF－41型”导弹俗称“东风快递”，速度可达到26马赫（1马赫＝340米/秒），则“DF－41型”导弹飞行多少分钟能打击到12000公里处的目标？设飞行 $x$ 分钟能打击到目标，可以得到方程（）

A、 $26 \times 340 \times 60 x = 12000$ B、 $26 \times 340 x = 12000$ C、 $\frac{26 \times 340 x}{1000} = 12000$ D、 $\frac{26 \times 340 \times 60 x}{1000} = 12000$

查看试题解析
6. 小明解方程 $\frac{x + 1}{2} - 1 = \frac{x - 2}{3}$ 的步骤如下：
解：方程两边同乘6，得 $3 (x + 1) - 1 = 2 (x - 2)$ ①
去括号，得 $3 x + 3 - 1 = 2 x - 2$ ②
移项，得 $3 x - 2 x = - 2 - 3 + 1$ ③
合并同类项，得 $x = - 4$ ④
以上解题步骤中，开始出错的一步是（）

A、① B、② C、③ D、④

查看试题解析
7. 《孙子算经》是中国传统数学的重要著作，其中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？”意思是：用一根绳子去量一根木头的长，绳子还剩余4.5尺；将绳子对折再量木头，则木头还剩余1尺，问木头长多少尺？可设木头长为x尺，绳子长为y尺，则所列方程组正确的是（）

A、 ${\begin{array}{l} y - x = 4.5 \\ 2 x - y = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4.5 \\ 2 x - y = 1 \end{array}$ C、 ${\begin{array}{l} x - y = 4.5 \\ \frac{y}{2} - x = 1 \end{array}$ D、 ${\begin{array}{l} y - x = 4.5 \\ x - \frac{y}{2} = 1 \end{array}$

查看试题解析
8. 已知二元一次方程组 ${\begin{matrix} 2 x - y = 5 \\ x - 2 y = 1 \end{matrix}$ ，则x﹣y的值为（）

A、2 B、6 C、﹣2 D、﹣6

查看试题解析
9. 关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x - y = 2 k - 3 \\ x - 2 y = k \end{array}$ 的解中 $x$ 与 $y$ 的和不小于5，则 $k$ 的取值范围为（）

A、 $k \geq 8$ B、 $k > 8$ C、 $k \leq 8$ D、 $k < 8$

查看试题解析

10. 某班环保小组收集废旧电池，数据统计如下表．问1节5号电池和1节7号电池的质量分别是多少？设1节5号电池的质量为x克，1节7号电池的质量为y克，列方程组，由消元法可得x的值为（）

	5号电池（节）	7号电池（节）	总质量（克）
第一天	2	2	72
第二天	3	2	96

A、12 B、16 C、24 D、26

查看试题解析

二、填空题（每空3分，共18分）

11. 推理是数学的基本思维方式、若推理过程不严谨，则推理结果可能产生错误.
例如，有人声称可以证明“任意一个实数都等于0”，并证明如下：
设任意一个实数为x，令 $x = m$ ，
等式两边都乘以x，得 $x^{2} = m x$ .①
等式两边都减 $m^{2}$ ，得 $x^{2} - m^{2} = m x - m^{2}$ .②
等式两边分别分解因式，得 $(x + m) (x - m) = m (x - m)$ .③
等式两边都除以 $x - m$ ，得 $x + m = m$ .④
等式两边都减m，得x＝0.⑤
所以任意一个实数都等于0.
以上推理过程中，开始出现错误的那一步对应的序号是.

查看试题解析
12. 我国古代数学经典著作《九章算术》中有这样一题，原文是：“今有共买物，人出八，盈三，人出七，不足四，问人数，物价各几何？”意思是：今有人合伙购物，每人出八钱，会多三钱；每人出七钱，又差四钱．问人数、物价各多少？设人数为x人，物价为y钱，可列方程组为
．

查看试题解析
13. 若实数m，n满足 $∣ m - n - 5 ∣ + \sqrt{2 m + n - 4} = 0$ ，则 $3 m + n =$ .

查看试题解析
14. 阅读材料：整体代值是数学中常用的方法.例如“已知 $3 a - b = 2$ ，求代数式 $6 a - 2 b - 1$ 的值.”可以这样解： $6 a - 2 b - 1 = 2 (3 a - b) - 1 = 2 \times 2 - 1 = 3$ .根据阅读材料，解决问题：若 $x = 2$ 是关于x的一元一次方程 $a x + b = 3$ 的解，则代数式 $4 a^{2} + 4 a b + b^{2} + 4 a + 2 b - 1$ 的值是.

查看试题解析
15. 幻方的历史很悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方（如图1），将9个数填在3×3（三行三列）的方格中，如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等，就得到一个广义的三阶幻方．图2的方格中填写了一些数字和字母，若能构成一个广义的三阶幻方，则mn＝．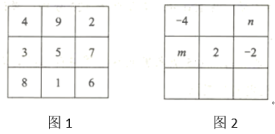

查看试题解析
16. 已知关于x，y的二元一次方程组 ${\begin{array}{l} 2 x + 3 y = 5 a \\ x + 4 y = 2 a + 3 \end{array}$ 满足 $x - y > 0$ ，则a的取值范围是.

查看试题解析

三、解答题（共9题，共72分）

17. 解方程： $\frac{x - 3}{2} - \frac{2 x + 1}{3}$ =1．

查看试题解析
18. 解方程： $x - \frac{x - 2}{2} = 1 - \frac{2 x - 1}{3}$

查看试题解析
19. 解方程组： ${\begin{cases} 3 x - 4 (x - 2 y) = 5 \\ x - 2 y = 1 \end{cases}$

查看试题解析
20. 解方程组： ${\begin{array}{l} 3 x + \frac{1}{2} y = 8 \\ 2 x - \frac{1}{2} y = 2 \end{array}$

查看试题解析
21. 已知方程组 ${\begin{array}{l} x + y = 3 ① \\ x - y = 2 ② \end{array}$ 的解满足 $2 k x - 3 y < 5$ ，求k的取值范围.

查看试题解析
22. 已知 $\frac{A}{x - 1} - \frac{B}{2 - x} = \frac{2 x - 6}{(x - 1) (x - 2)}$ ，求A、B的值.

查看试题解析
23. 端午节前夕，某超市从厂家分两次购进 $A$ 、 $B$ 两种品牌的粽子，两次进货时，两种品牌粽子的进价不变.第一次购进 $A$ 品牌粽子100袋和 $B$ 品牌粽子150袋，总费用为7000元；第二次购进 $A$ 品牌粽子180袋和 $B$ 品牌粽子120袋，总费用为8100元.

(1)、求 $A$ 、 $B$ 两种品牌粽子每袋的进价各是多少元；

(2)、当 $B$ 品牌粽子销售价为每袋54元时，每天可售出20袋，为了促销，该超市决定对 $B$ 品牌粽子进行降价销售.经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋.当 $B$ 品牌粽子每袋的销售价降低多少元时，每天售出 $B$ 品牌粽子所获得的利润最大？最大利润是多少元？

查看试题解析
24. 钢钢准备在重阳节购买鲜花到敬老院看望老人，现将自己在劳动课上制作的竹篮和陶罐拿到学校的“跳蚤市场”出售，以下是购买者的出价：

(1)、根据对话内容，求钢钢出售的竹篮和陶罐数量；

(2)、钢钢接受了钟钟的报价，交易后到花店购买单价为5元/束的鲜花，剩余的钱不超过20元，求有哪几种购买方案．

查看试题解析
25. 为贯彻执行“德、智、体、美、劳”五育并举的教育方针，内江市某中学组织全体学生前往某劳动实践基地开展劳动实践活动.在此次活动中，若每位老师带队30名学生，则还剩7名学生没老师带；若每位老师带队31名学生，就有一位老师少带1名学生.现有甲、乙两型客车，它们的载客量和租金如表所示：

甲型客车
乙型客车
载客量（人/辆）
35
30
租金（元/辆）
400
320
学校计划此次劳动实践活动的租金总费用不超过3000元.

(1)、参加此次劳动实践活动的老师和学生各有多少人？

(2)、每位老师负责一辆车的组织工作，请问有哪几种租车方案？

(3)、学校租车总费用最少是多少元？

查看试题解析

	甲型客车	乙型客车
载客量（人/辆）	35	30
租金（元/辆）	400	320