人教版备考2023中考数学二轮复习专题8 一元二次方程

试卷更新日期：2023-01-05 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（）

A、 $2 x^{2} = 5 x - 1$ B、 $x + \frac{1}{x} = 2$ C、 $(x - 3) (x + 1) = x^{2} - 5$ D、 $3 x - y = 5$

查看试题解析
2. 已知 $x = 1$ 是关于x的一元二次方程 $x^{2} + m x = 0$ 的一个根，则m的值是（）

A、-1 B、0 C、1 D、2

查看试题解析
3. 一元二次方程 $x^{2} - 6 x - 11 = 0$ 配方后是（）

A、 ${(x - 3)}^{2} = 2$ B、 ${(x - 3)}^{2} = 20$ C、 ${(x + 3)}^{2} = 2$ D、 ${(x + 3)}^{2} = 20$

查看试题解析
4. 关于x的一元二次方程 $(a - 1) x^{2} + 3 x - 2 = 0$ 有实数根，则a的取值范围是（）

A、 $a > - \frac{1}{8}$ B、 $a \geq - \frac{1}{8}$ C、 $a > - \frac{1}{8} ， a \neq 1$ D、 $a \geq - \frac{1}{8} ， a \neq 1$

查看试题解析
5. 2021年七月份某地有牲猪感染猪瘟100头，后来八、九月份感染猪瘟的共有231头，设八，九月份平均每月猪瘟的感染增长率为x，依题意列出的方程是（）

A、 $100 (1 + x)^{2} = 231$ B、 $100 (1 + x) + 100 (1 + x)^{2} = 231$ C、 $100 + 100 (1 + x)^{2} = 231$ D、 $100 + 100 (1 + x) + 100 (1 + x)^{2} = 231$

查看试题解析
6. 已知关于x的一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两实数根分别为 $x_{1} ， x_{2}$ ，则 $x_{1} x_{2} + x_{1} + x_{2}$ 的值为（）

A、 $- 1$ B、1 C、5 D、 $- 5$

查看试题解析
7. 在宽为30m，长为80m的矩形耕地上，修筑同样宽的三条道路（两条纵向，一条横向，横向与纵向互相垂直），把耕地分成六块作试验田，要使试验田总面积为1998平方米，问道路应为多宽？若设道路宽为xm，则根据题意可列方程来求解（）

A、 $30 \times 80 - 30 \times 2 x - 80 x = 1998$ B、 $30 \times 80 - 30 \times 2 x - 80 x - 2 x^{2} = 1998$ C、 $30 \times 80 - (30 - x) (80 - 2 x) = 1998$ D、 $(30 - x) (80 - 2 x) = 1998$

查看试题解析
8. 已知关于x的一元二次方程 $(p + 1) x^{2} + 2 q x + (p + 1) = 0$ （其中p，q为常数）有两个相等的实数根，则下列结论中，错误的是（）．

A、1可能是方程 $x^{2} + q x + p = 0$ 的根 B、-1可能是方程 $x^{2} + q x + p = 0$ 的根 C、0可能是方程 $x^{2} + q x + p = 0$ 的根 D、1和-1都是方程 $x^{2} + q x + p = 0$ 的根

查看试题解析
9. 下列命题：① 若b＝a＋c时，一元二次方程 $a x^{2} + b x + c = 0$ 一定有实数根；② 若方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根，则方程 $c x^{2} + b x + a = 0$ 也一定有两个不相等实数根；③ 若二次函数 $y = a x^{2} + c$ ，当取 $x_{1}$ 、 $x_{2}$ （ $x_{1} \neq x_{2}$ ）时，函数值相等，则当x取 $x_{1} + x_{2}$ 时函数值为0；④ 若 $b^{2} - 4 a c > 0$ ，则二次函数 $y = a x^{2} + b x + c$ 的图像与坐标轴的公共点的个数是2或3，其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

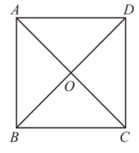
10. 关于 $x$ 的一元二次方程 $x^{2} - (k - 1) x - k + 2 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，若 $(x_{1} - x_{2} + 2) (x_{1} - x_{2} - 2) + 2 x_{1} x_{2} = - 3$ ，则 $k$ 的值．

查看试题解析
11. 喜迎2022年10月16日“二十大”的召开，某公司为了贯彻“发展低碳经济，建设美丽中国”的理念，对其生产设备进行了升级改造，不仅提高了产能，而且大幅降低了碳排放量．已知该公司七月份的产值为200万元，第三季度的产值为720万元，设公司每月产值的平均增长率相同且为 $x$ ，则根据题意列出的方程是．

查看试题解析
12. 一元二次方程 $(k + 1) x^{2} - 3 x + 2 = 0$ 有实数根，则k的取值范围是．

查看试题解析
13. 规定：在实数范围内定义一种运算☆，其规则是 $a ☆ b = a^{2} - b^{2}$ ，若 $(x - 2) ☆ 3 = 0$ ，则 $x$ 的值为.

查看试题解析
14. 定义：若两个一元二次方程有且只有一个相同的实数根，我们就称这两个方程为“同伴方程”．例如 $x^{2} = 4$ 和 $(x - 2) (x + 3) = 0$ 有且仅有一个相同的实数根 $x = 2$ ，所以这两个方程为“同伴方程”．若关于x的方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的参数同时满足 $a + b + c = 0$ 和 $a - b + c = 0$ ，且该方程与 $(x + 2) (x - n) = 0$ 互为“同伴方程”，则 $n =$ ．

查看试题解析
15. 写出一个一元二次方程，使它的一个根为1，另一个根为 $- \sqrt{2}$ ，这个方程的一般式是．

查看试题解析
16. 如图，在正方形ABCD中，AB＝6，连接对角线AC、BD相交于点O，点P是正方形边上或对角线上的一点，若 $\frac{P D}{A P} = 2$ ，则AP＝．

查看试题解析

三、计算题

17. 解方程： $2 {(x + 3)}^{2} = x (x + 3)$ ．

查看试题解析

四、解答题

18. 若关于x的一元二次方程 $(m - 1) x^{2} - 4 m x + 4 m + 6 = 0$ 有实数根，求m能取的正整数值．

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - m x + m - 1 = 0$ ．求证：方程总有两个实数根．

查看试题解析
20. 某平台网店销售医用外科口罩，每盒售价 $60$ 元，每星期可卖 $300$ 盒，为了便民利民，该网店决定降价销售，市场调查反映：每降价1元，每星期多卖 $30$ 盒，已知该款口罩每盒成本价为 $40$ 元，若该网店想一星期获利 $6480$ 元，且尽快减少库存，那么这星期预期销售多少盒口罩？

查看试题解析

五、综合题

21. 已知关于x的方程 $x^{2} - (m + 1) x + m = 0$ .

(1)、判断该方程是否有实数根？

(2)、设此方程的两实数根为 $x_{1}$ ， $x_{2}$ ，且 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{2}{3}$ ，求m的值．

查看试题解析
22. 嘉淇同学用配方法推导一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的求根公式时，对于 $b^{2} - 4 a c > 0$ 的情况，她是这样做的：
由于 $a \neq 0$ ，方程 $a x^{2} + b x + c = 0$ 变形为：
$x^{2} + \frac{b}{a} x = - \frac{c}{a}$ ， ……第一步
$x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2} = - \frac{c}{a} + {(\frac{b}{2 a})}^{2}$ ， ……第二步
${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$ ， ……第三步
$x + \frac{b}{2 a} = \sqrt{\frac{b^{2} - 4 a c}{4 a^{2}}}$ ， ……第四步
$x = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a}$ ． ……第五步

(1)、嘉淇的解法从第步开始出现错误；事实上，当 $b^{2} - 4 a c > 0$ 时，方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的求根公式是；

(2)、用配方法解方程： $x^{2} - 2 x - 24 = 0$ ．

查看试题解析
23. 某片果园有果树100棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果y（千克），增种果树x（棵），它们之间的函数关系为： $y = - \frac{1}{2} x + 80$ ．

(1)、在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实8250千克？

(2)、当增种果树多少棵时，果园的总产量w（千克）最大？最大产量是多少？

查看试题解析

人教版备考2023中考数学二轮复习 专题8 一元二次方程

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

人教版备考2023中考数学二轮复习专题8 一元二次方程