广东省深圳市2021-2022学年第二学期学科素养形成八年级数学阶段测试一
试卷更新日期：2023-01-05 类型：月考试卷
一、选择题(共10小题，共30分)
-
1. 若3m-5x3+m>4是关于x的一元一次不等式，则m的值是（ ）A、-3 B、-2 C、0 D、12. 已知△ABC的三个内角分别为∠A、∠B、∠C，三边分别为a、b、c，下列条件不能判定△ABC是直角三角形的是（ ）A、∠A：∠B：∠C=3：4：7 B、∠A=∠B-∠C C、a：b：c=2：3：4 D、b2=(a+c) (a-c)3. 已知a<b，下列不等式中，变形正确的是（ ）A、a-3>b-3 B、 C、3a-1>3b-1 D、-3a>-3b4. 如图，∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于（ ）
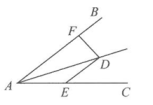A、10 B、7 C、5 D、45. 如图，△ABC中，AB=AC，∠BAC=120°，BC=2 ， D为BC的中点，DE⊥AB，则△EBD的面积为（ ）
A、 B、 C、 D、6. 实数a，b，c在数轴上的对应点的位置如图所示，若|a|>|b|，则下列结论一定成立的时（ ）
A、b+c>0 B、a+c<-2 C、<1 D、abc≥07. 下列说法中，正确的是（ ）A、在角的内部到角的两边距离相等的点一定在这个角的平分线上 B、一个三角形两边的垂直平分线的交点到这个三角形三边的距离相等 C、“若a>b，则a2>b2”的逆命题是真命题 D、用反证法证明“三角形中必有一个角不大于60°”，先假设这个三角形中有一个内角大于60°8. 设“○”“□”“△”分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个“○”"□”“△”按质量从小到大的排列顺序为（ ）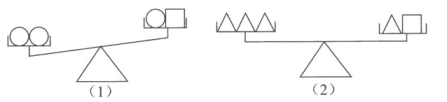
A、○□△ B、○△□ C、□○△ D、△□○9. 如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠CAD的度数为（ ）
A、35° B、40° C、45° D、50°10. 如图，点P为定角∠AOB平分线上的一个定点，且∠MPN与∠4OB互补．若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM= PN；②OM+ON的值不变；③MN的长不变；④四边形PMON的面积不变，其中，正确的结论是（ ）
A、①②③ B、②③④ C、①③④ D、①②④二、填空题(每题3分，共15分)
-
11. 等腰三角形的两边长是6cm和3cm，那么它的周长是12. x的与x的和不超过5用不等式可以表示为13. 如图，直线y=kx+b经过点A (-3，2)，B(1，0)，则关于x的不等式kx+b<2的解集为
14. 如图，在△ABC中，O是△ABC内一点，且点O到△ABC三边的距离相等，∠BOC=134°，则∠A的度数为
15. 如图中的螺旋由一系列直角三角形组成，则第n个三角形的面积为 ．
三、解答题(共55分)
-
16. 如图，在△ABC中，AD平分∠BAC，∠C=90°，DE⊥AB于点E，BD=DF，求证： CF=EB．
17. 解不等式组 把解集表示在数轴上，并求出不等式组的整数解．18. 如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，点E是AB的中点，连接DE．求证：△ABD是等腰三角形．
19. 如图，在△ABC中，∠C=90°．
(1)、用尺规作图，在AC边上找一点D，使DB+DC=AC(保留作图痕迹，不要求写作法和证明)；(2)、在(1)的条件下若AC=6，AB=8，求DC的长．20. 以下是两位同学在复习不等式过程中的对话：小明说：”不等式a> 2a永远都不会成立，因为如果在这个不等式两边同时除以a，就．会出现1>2这样的错误结论!”
小丽说：“如果a>b，c>d，那么一定会得出a-c>b-d．"
你认为小明的说法(填“正确”或“不正确”)；小丽的说法(填“正确”或“不正确”)，并选择其中一个人判断阐述你的理由(若认为正确，则进行证明；若认为不正确，则给出反例)．
