人教版备考2023中考数学二轮复习专题6 二元一次方程组

试卷更新日期：2023-01-05 类型：二轮复习

进入出卷网下载

一、单选题

1. 将方程2x+y＝5写成含x的式子表示y的形式，正确的是（）

A、y＝2x﹣5 B、y＝5﹣2x C、x＝ $\frac{x}{2} - \frac{5}{2}$ D、x＝ $\frac{5}{2} - \frac{x}{2}$

查看试题解析
2. 若y-2x＝0，则x：y等于（　　）

A、1：2 B、1：4 C、2：1 D、4：1

查看试题解析
3. 用加减法解方程组 ${\begin{cases} 2 x - y = 2 ① \\ x + y = 4 ② \end{cases}$ 时，方程①+②得（）

A、2y＝2 B、3x＝6 C、x﹣2y＝﹣2 D、x+y＝6

查看试题解析
4. 定义运算“ ✱ ”，规定 $x*y = {ax}^{2} + by$ (其中 $a 、 b$ 为常数)，若已知 $1 * 2 = 5 ， 2 * 1 = 6$ ，则 $2 * 3$ 的值为（）

A、10 B、9 C、8 D、7

查看试题解析
5. 小华和爸爸一起玩“掷飞镖”游戏，游戏规则：站在5米开外朝飞镖盘扔飞镖，若小华投中1次得5分，爸爸投中1次得3分，结果两人一共投中了20次，经过计算发现爸爸的得分比小华的得分多4分.设小华投中的次数为 $x$ 次，爸爸投中的次数为 $y$ 次，根据题意列出的方程组正确的是（）

A、 ${\begin{cases} x + y = 20 \\ 3 x + 4 = 5 y \end{cases}$ B、 ${\begin{cases} x + y = 20 \\ 3 x + 5 y = 4 \end{cases}$ C、 ${\begin{cases} x + y = 20 \\ 5 x = 3 y + 4 \end{cases}$ D、 ${\begin{cases} x + y = 20 \\ 5 x + 4 = 3 y \end{cases}$

查看试题解析
6. 下列方程中，①x+y=6；②x(y+1)=6；③3x+y=z+1；④mn+m=7，是二元一次方程的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程ax-2y=6的一个解，那么a的值是（）

A、-10 B、-9 C、9 D、10

查看试题解析
8. 如图，在数轴上，点、分别表示数a、b，且a+b=2．若AB=4，则点表示的数为（）

A、-1 B、-2 C、2 D、1

查看试题解析
9. 已知 $t = x^{2} - 2 x + 4 ， x ， y$ 满足 ${\begin{array}{l} x - y = m + 1 \\ x + y = 3 m + 3 \end{array}$ ，且 $- 1 \leq y \leq 1$ ，则 $t$ 的取值范围是（）

A、 $4 \leq t \leq 12$ B、 $3 \leq t \leq 12$ C、 $3 \leq t \leq 4$ D、 $4 \leq t \leq 7$

查看试题解析
10. 在《九章算术》中，一次方程组是由算筹布置而成的．如图1所示的算筹图，表示的方程组就是 ${\begin{cases} 2 x + y = 11 ， \\ 4 x + 3 y = 27 ， \end{cases}$ 类似地，图2所示的算筹图表示的方程组为（）

A、 ${\begin{cases} 3 x + 2 y = - 14 ， \\ x + 4 y = 23 \end{cases}$ B、 ${\begin{cases} 3 x + 2 y = - 9 ， \\ x + 4 y = 23 \end{cases}$ C、 ${\begin{cases} 3 x + 2 y = 19 ， \\ x + 4 y = 3 \end{cases}$ D、 ${\begin{cases} 3 x + 2 y = 19 ， \\ x + 4 y = 23 \end{cases}$

查看试题解析

二、填空题

11. 写出二元一次方程 $3 x - y = 4$ 的一组解。（写出一组即可）

查看试题解析
12. 如图，把7个相同的小长方形放入大长方形中，则阴影部分的面积是。

查看试题解析
13. 若 $(2 x + y - 5)^{2} + \sqrt{x + 2 y + 4} = 0$ ，则x-y的值是．

查看试题解析
14. 已知x，y满足|x-5|+(x-y-1)²=0，则 ${(x - y)}^{2021}$ 的值是.

查看试题解析
15. 设甲、乙两车在同一直线公路上匀速行驶，开始甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车的货物转给甲车，然后甲车继续前行，乙车向原地返回.设x秒后两车间的距离为y米，y关于x的函数关系如图所示，则乙车的速度是米/秒.

查看试题解析
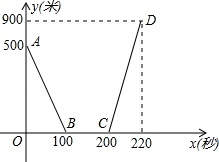16. 为实现营养的合理搭配，某电商推出适合不同人群的甲、乙两种袋装混合粗粮．其中，甲种粗粮每袋装有3千克 $A$ 粗粮，1千克 $B$ 粗粮，1千克 $C$ 粗粮；乙种粗粮每袋装有1千克 $A$ 粗粮，2千克 $B$ 粗粮，2千克 $C$ 粗粮．甲、乙两种袋装粗粮每袋成本价分别为袋中的 $A$ ， $B$ ， $C$ 三种粗粮的成本价之和．已知 $A$ 粗粮每千克成本价为 $6$ 元，甲种粗粮每袋售价为58.5元，利润率为30%，乙种粗粮的利润率为20%若这两种袋装粗粮的销售利润率达到24%，则该电商销售甲、乙两种袋装粗粮的数量之比是.（商品的利润率 $= \frac{商品的售价 - 商品的成本价}{商品的成本价} \times 100 %$ ）

查看试题解析

三、计算题

17. 解方程组 ${\begin{array}{l} 2 x + 3 y = 17 ① \\ x - 2 y = 5 ② \end{array}$

查看试题解析

四、解答题

18. “鸡兔同笼”是我国古代著名的数学趣题之一，大约在1500年前成书的《孙子算经》中，就有关于“鸡兔同笼”的记载：“今有雏兔同笼，上有三十五头，下有九十四足，问雏兔各几何?"这四句话的意思是：有若干只鸡兔关在一个笼子里，从上面数，有35个头；从下面数，有94条腿，问笼中鸡和兔分别有多少只?

查看试题解析
19. 已知正数 $a$ 的两个平方根x，y为方程4x-3y=28的一组解，求 $a$ 的值.

查看试题解析
20. 在△ABC中，三边长分别为a，b，c，且满足 ${(a - \sqrt{8})}^{2}$ + $\sqrt{b - 4}$ +|c﹣2 $\sqrt{6}$ |=0，判断△ABC是否构成直角三角形，并说明理由．

查看试题解析

五、综合题

21. 已知 $a 、 b$ 为常数，且满足 $| a - 12 | + {(b + 20)}^{2} = 0$ ，其中 $a 、 b$ 分别为点A、点B在数轴上表示的数，如图所示，动点 $E 、 F$ 分别从 $A 、 B$ 同时开始运动，点E以每秒 $6$ 个单位向左运动，点F以每秒 $2$ 个单位向右运动，设运动时间为 $t$ 秒．

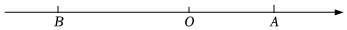(1)、求a、b的值：

(2)、请用含t的代数式表示点E在数轴上对应的数为：；点F在数轴上对应的数为：；

(3)、当E、F相遇后，点E继续保持向左运动，点F在原地停留 $4$ 秒后向左运动且速度变为原来的 $5$ 倍，在整个运动过程中，当E、F之间的距离为 $2$ 个单位时，请直接写出运动时间t的值．

查看试题解析
22. 对任意一个三位数 $m$ ，如果 $m$ 满足各数位上的数字互不相同且都不为0，则称 $m$ 为“称心数”．将一个“称心数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为 $Q (m)$ ．例如 $m = 124$ ，对调百位与十位上的数字得到214，对调百位与个位上的数字得到421，对调十位与个位上的数字得到142，这三个新三位数的和为 $214 + 421 + 142 = 777$ ， $777 \div 111 = 7$ ，所以 $Q (124) = 7$ ．

(1)、直接写出最小和最大的“称心数 $m$ ”；

(2)、若 $m$ 、 $n$ 都是“称心数”，其中 $m = 100 x + 32$ ， $n = 150 + y (1 ⩽ x ⩽ 9$ ， $1 ⩽ y ⩽ 9$ ， $x$ 、 $y$ 都是正整数），当 $Q (m) + Q (n) = 18$ 时，求 $\frac{Q (m)}{Q (n)}$ 的值．

查看试题解析

人教版备考2023中考数学二轮复习 专题6 二元一次方程组

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

人教版备考2023中考数学二轮复习专题6 二元一次方程组