人教版备考2023中考数学二轮复习专题2 整式与因式分解

试卷更新日期：2023-01-05 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列算式中，正确的是（）

A、 $a^{4} + a^{2} = a^{6}$ B、 $- a^{3} \cdot a^{5} = - a^{8}$ C、 ${(- a^{2})}^{6} = - a^{12}$ D、 ${(3 a^{2})}^{3} = 9 a^{6}$

查看试题解析
2. 若 $x = \frac{1}{2}$ ，则代数式 $2 x^{2} - 5 x + x^{2} + 4 x - 3 x^{2} - 2$ 的值为（）

A、 $\frac{5}{2}$ B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、 $- \frac{5}{2}$

查看试题解析
3. 下列各组中的两个单项式，是同类项的是（）

A、 $a^{2}$ 与 $2 a$ B、 $- 0.5 a b$ 与 $\frac{1}{2} b a$ C、 $a^{2} b$ 与 $a b^{2}$ D、a与b

查看试题解析
4. 若多项式 $2 x^{2} + a x - 6$ 能分解成两个一次因式的积，且其中一个次因式 $2 x - 3$ ，则 $a$ 的值为（）

A、1 B、5 C、-1 D、-5

查看试题解析
5. 要使（x²＋ax＋1）（x－2）的结果中不含x²项，则a为（）

A、－2 B、0 C、1 D、2

查看试题解析
6. 已知 $3^{x} = 4 ， 3^{y} = 6 ， 3^{z} = 12$ ，则x、y、z三者之间关系正确的是（）

A、xy=2z B、x+y=2z C、x+2y=2z D、x+2y=z

查看试题解析
7. 下列等式中，从左到右的变形是因式分解（）

A、 $2 x^{2} y + 8 x y^{2} + 6 = 2 x y (x + 4 y) + 6$ B、 $(5 x - 1) (x + 3) = 5 x^{2} - 14 x - 3$ C、 $x^{2} - y^{2} = (x + y) (x - y)$ D、 $x^{3} + y^{2} + 2 x + 1 = {(x + 1)}^{2} + y^{2}$

查看试题解析
8. 如图，长方形ABCD的周长是12厘米，以、AB、BC为边向外作正方形ABGH和正方形BCEF，如果正方形ABGH和正方形BCEF的面积之和为18平方厘米，那么长方形ABCD的面积是（）

A、6平方厘米 B、8平方厘米 C、9平方厘米 D、10平方厘米

查看试题解析
9. 若a、b、c、d是正整数，且a+b＝20，a+c＝24，a+d＝22，设a+b+c+d的最大值为M，最小值为N，则M﹣N＝（）

A、28 B、12 C、48 D、36

查看试题解析
10. 对任意一个两位数n，如果n满足个位与十位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”的十位上的数字与个位上的数字互换位置后，得到一个新两位数：把所得的新两位数与原两位数的和与11的商记为F（n）．例如n＝23．互换十位与个位上的数字得到32，所得的新两位数与原两位数的和为23+32＝55，55÷11＝5，所以F（23）＝5．若s，t都是“相异数”，其中s＝10x+3，t＝50+y（1≤x≤9，1≤y≤9．x，y都是正整数），当F（s）+F（t）＝15时，则 $\frac{F (s)}{F (t)}$ 的最大值为（）

A、2 B、 $\frac{3}{2}$ C、 $\frac{11}{4}$ D、4

查看试题解析

二、填空题

11. 因式分解： $25 m^{2} - 10 m n + n^{2} =$ ．

查看试题解析
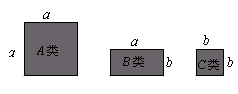
12. 将代数式 $2 a^{2} b$ 、 $- \frac{2}{3} b^{2} a$ 、 $3 a b$ 、 $- \frac{3}{2} b a^{2}$ 中的同类项合并得．

查看试题解析
13. 用图中所示的正方形和长方形卡片若干张，拼成一个长为2a+b，宽为3a+2b的矩形，需要A类卡片张，B类卡片张，C类卡片张．

查看试题解析
14. 观察下列各式： $(x - 1) (x + 1) = x^{2} - 1$ ； $(x - 1) (x^{2} - x + 1) = x^{3} - 1$ ； $(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；……根据前面各式的规律可得到 $(x - 1) (x^{n} + x^{n - 1} + x^{n - 2} + ⋯ + x + 1) =$ ．

查看试题解析
15. 如图，用正方形方框在日历中任意框出4个数，设其中最小的数为x，那么这4个数之和为．
星期一
星期二
星期三
星期四
星期五
星期六
星期日

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

查看试题解析
16. 如图，把五个长为b，宽为a（b>a)的小长方形，按图一和图二两种方式放在一个长比宽大 $(6 - a)$ 的大长方形上，设图一中两块阴影部分的周长和为 $C_{1}$ ，图2中阴影部分的周长和为 $C_{2}$ ，则 $C_{2} - C_{1}$ 的值为.

查看试题解析

三、计算题

17. 计算：

(1)、 $(2 a + 3 b) (2 a - 3 b) - {(a - 3 b)}^{2}$ ；

(2)、 $(9 x^{3} y - 12 x y^{3} + 3 x y^{2}) \div (- 3 x y) - (2 y + x) (2 y - x)$ ．

查看试题解析
18. 因式分解：

(1)、 $x^{2} (a - b) + 9 (b - a)$

(2)、 ${(a^{2} + 4)}^{2} - 16 a^{2}$

查看试题解析

四、解答题

19. 先化简，再求值： $(2 x - 3 y) (x + 2 y) + 2 (x + 2 y) (x - 2 y) - {(2 x - 3 y)}^{2}$ ，其中 $x = 2$ ， $y = 1$ ．

查看试题解析
20. 已知二次三项式 $x^{2} - 2 x + 3$ 与多项式 $a x + b$ （a、b为常数）相乘，积中不出现二次项，且一次项系数为 $- 1$ ，求 $a$ 、 $b$ 的值．

查看试题解析
21. 已知一个数比 $a$ 的6倍大3，另一个数比 $a$ 的7倍小5．求前一个数减去后一个数的差．

查看试题解析

五、综合题

22. 已知 $A = (4 x^{4} - x^{2}) \div x^{2}$ ， $B = (2 x + 5) (2 x - 5) + 1$ ．

(1)、求 $A$ 和 $B$ ；

(2)、若变量 $y$ 满足 $y - A = B$ ，求 $y$ 与 $x$ 的关系式；

(3)、在（2）的条件下，当 $y = 7$ 时，求 $8 x^{2} + {(8 x^{2} - y)}^{2} - 30$ 的值．

查看试题解析

23. 阅读下面材料，在代数式中，我们把一个二次多项式化为一个完全平方式与一个常数的和的方法叫做配方法。配方法是一种重要的解决问题的数学方法，它不仅可以将一个看似不能分解的多项式因式分解，还能求代数式最大值，最小值等问题．

例如：求代数式： $x^{2} - 12 x + 2020$ 的最小值

解：原式 $= x^{2} - 12 x + 6^{2} - 6^{2} + 2020$

$= {(x - 6)}^{2} + 1984$

∵ ${(x - 6)}^{2} \geq 0$

∴当x=6时， ${(x - 6)}^{2}$ 的值最小，最小值为0

∴ ${(x - 6)}^{2} + 1984 \geq 1984$

∴当 ${(x - 6)}^{2} = 0$ 时， ${(x - 6)}^{2} + 1984$ 的值最小，最小值为1984

∴代数式： $x^{2} - 12 x + 2020$ 的最小值是1984

例如：分解因式： $x^{2} - 120 x + 3456$

解：原式 $= x^{2} - 2 \times 60 x + 6 0^{2} - 6 0^{2} + 3456$

$= {(x - 60)}^{2} - 144$

$= {(x - 60)}^{2} - 1 2^{2}$

$= (x - 60 + 12) (x - 60 - 12)$

$= (x - 48) (x - 72)$

(1)、分解因式

x^{2} - 46 x + 520

；

(2)、若

y = - x^{2} + 2 x + 1313

，求y的最大值；

(3)、当m，n为何值时，代数式

m^{2} - 2 m n - 2 m + 2 n^{2} - 4 n + 2030

有最小值，并求出这个最小值．

查看试题解析