2023年中考数学精选真题实战测试10 二次根式B

试卷更新日期：2023-01-04 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列各式计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 2 = \sqrt{6}$

查看试题解析
2. 下列根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{9}}$ B、 $\sqrt{4}$ C、 $\sqrt{a^{2}}$ D、 $\sqrt{a + b}$

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{3} + \sqrt{3} = 3$ B、 $4 \sqrt{5} - \sqrt{5} = 4$ C、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ D、 $\sqrt{32} \div \sqrt{8} = 4$

查看试题解析
4. 实数a、b在数轴上的位置如图所示，化简 $\sqrt{{(a + 1)}^{2}} + \sqrt{{(b - 1)}^{2}} - \sqrt{{(a - b)}^{2}}$ 的结果是（）．

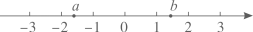A、-2 B、0 C、-2a D、2b

查看试题解析
5. 估计 $\sqrt{3} \times (2 \sqrt{3} + \sqrt{5})$ 的值应在（）

A、10和11之间 B、9和10之间 C、8和9之间 D、7和8之间

查看试题解析
6. 函数 $y = \sqrt{2 - x} + \frac{1}{x + 1}$ 中，自变量 $x$ 的取值范围是（）

A、 $x ⩽ 2$ B、 $x ⩽ 2$ 且 $x \neq - 1$ C、 $x ⩾ 2$ D、 $x ⩾ 2$ 且 $x \neq - 1$

查看试题解析
7. 计算： $(\frac{\sqrt{5} + 1}{2} - 1) \cdot \frac{\sqrt{5} + 1}{2} =$ （）

A、0 B、1 C、2 D、 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
8. 下列计算正确的是（）

A、 $\sqrt{2^{2}} = 2$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $\sqrt{2^{2}} = \pm 2$ D、 $\sqrt{{(- 2)}^{2}} = \pm 2$

查看试题解析
9. 已知 $\sqrt{a - 2} + | b - 2 a | = 0$ ，则a+2b的值是（）

A、4 B、6 C、8 D、10

查看试题解析
10. 估计 $(2 \sqrt{3} + 3 \sqrt{2}) \times \sqrt{\frac{1}{3}}$ 的值应在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析

二、填空题（每空3分，共18分）

11. 若 $\sqrt{{(1 - a)}^{2}} = a - 1$ ，则a的取值范围是．

查看试题解析
12. 已知 $y = \sqrt{2 x - 1} + \sqrt{1 - 2 x} + \frac{1}{3}$ ，则 $x - y =$ ．

查看试题解析
13. 我们把宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ 的矩形叫做黄金矩形.黄金矩形给我们以协调、匀称的美感，世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计.已知四边形ABCD是黄金矩形，边AB的长度为 $\sqrt{5} -$ 1，则该矩形的周长为 .

查看试题解析
14. 若两个代数式 $M$ 与 $N$ 满足 $M \cdot N = - 1$ ，则称这两个代数式为“互为友好因式”，则 $\sqrt{3} - \sqrt{5}$ 的“互为友好因式”是．

查看试题解析
15. 已知a是 $\sqrt{10}$ 的整数部分，b是它的小数部分，则2a+b- $\sqrt{10}$ ＝.

查看试题解析
16. 对于两个不相等的实数a，b，定义一种新的运算如下： $a * b = \frac{\sqrt{a + b}}{a - b} (a + b > 0)$ ，如 $3 * 2 = \frac{\sqrt{3 + 2}}{3 - 2} = \sqrt{5}$ ，则 $8 * (6 * 3) =$ ．

查看试题解析

三、解答题（共9题，共72分）

17. 计算： $\sqrt{3}$ （1﹣ $\sqrt{3}$ ）+ $\sqrt{12}$ +（ $\frac{1}{3}$ ）^﹣1 ．

查看试题解析
18. 计算 $(\sqrt{2} + 1) (\sqrt{2} - 1) +^{3} \sqrt{- 8} + \sqrt{9}$

查看试题解析
19. 计算： ${(\sqrt{3} - 2)}^{2} + \sqrt{12} + 6 \sqrt{\frac{1}{3}}$

查看试题解析
20. 计算： ${(π - 3.14)}^{0} - {(\frac{1}{2})}^{- 2} + \sqrt[3]{27} - \sqrt{8}$ ．

查看试题解析
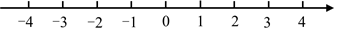21. 用※定义一种新运算：对于任意实数m和n ，规定 $m ※ n = m^{2} n - m n - 3 n$ ，如： $1 ※ 2 = 1^{2} \times 2 - 1 \times 2 - 3 \times 2 = - 6$ ．

(1)、求 $(- 2) ※ \sqrt{3}$ ；

(2)、若 $3 ※ m \geq - 6$ ，求m的取值范围，并在所给的数轴上表示出解集．

查看试题解析
22. 请仔细观察计算过程，完成下列问题：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
$\frac{1}{2 + \sqrt{3}} = \frac{1 \times (2 - \sqrt{3})}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3} ；$ ；
......

(1)、 $\frac{1}{\sqrt{6} + \sqrt{5}} =$ ；

(2)、 $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ （ $n$ 为正整数）；

(3)、求 $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \dots + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ 的值．

查看试题解析
23. 先阅读下列的解答过程，然后再解答：
形如 $\sqrt{m \pm 2 \sqrt{n}}$ 的化简，只要我们找到两个正数 $a 、 b$ ，使 $a + b = m$ ， $a b = n$ ，使得 $(\sqrt{a})^{2} + (\sqrt{b})^{2} = m$ ， $\sqrt{a} \cdot \sqrt{b} = n$ ，那么便有： $\sqrt{m \pm 2 \sqrt{n}} = \sqrt{(\sqrt{a} \pm \sqrt{b})^{2}} = \sqrt{a} \pm \sqrt{b}$ （ $a > b$ ）．
例如：化简 $\sqrt{7 + 4 \sqrt{3}}$
解：首先把 $\sqrt{7 + 4 \sqrt{3}}$ 化为 $\sqrt{7 + 2 \sqrt{12}}$ ，这里 $m = 7 ， n = 12$ ，由于 $4 + 3 = 7 ， 4 \times 3 = 12$ ，
即 $(\sqrt{4})^{2} + (\sqrt{3})^{2} = 7$ ， $\sqrt{4} \times \sqrt{3} = 12$ ，
∴ $\sqrt{7 + 4 \sqrt{3}} = \sqrt{7 + 2 \sqrt{12}} = \sqrt{(\sqrt{4} + \sqrt{3})^{2}} = 2 + \sqrt{3}$ ．

(1)、根据以上例子，请填空 $\sqrt{6 - 2 \sqrt{5}}$ =； $\sqrt{10 + 4 \sqrt{6}}$ =；

(2)、化简， $\sqrt{38 - 10 \sqrt{13}} - \sqrt{29 - 8 \sqrt{13}}$

查看试题解析
24. 观察下列各式：
① $\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ；② $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ；③ $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3} \dots$

(1)、请根据以上规律，写出第4个式子：.

(2)、请根据以上规律，写出第 $n$ 个式子：.

(3)、根据以上规律计算下列式子的值： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2022} + \sqrt{2021}}$ .

查看试题解析
25. 爱动脑筋的小明在做二次根式的化简时，发现一些二次根式的被开方数是二次三项式，而且这些二次三项式正好是完全平方式的结构，于是就可以利用二次根式的性质： $\sqrt{a^{2}} = | a | = {\begin{array}{l} a (a \geq 0) ， \\ - a (a < 0) \end{array}$ 来进一步化简．
比如： $\sqrt{x^{2} + 2 x + 1} = \sqrt{{(x + 1)}^{2}} = | x + 1 |$ ，
∴当 $x + 1 \geq 0$ 即 $x \geq - 1$ 时，原式 $= x + 1$ ；当 $x + 1 < 0$ 即 $x < - 1$ 时，原式 $= - x - 1$ ．

(1)、仿照上面的例子，请你尝试化简 $\sqrt{m^{2} - m + \frac{1}{4}}$ ．

(2)、判断甲、乙两人在解决问题：“ $a = 9$ ，求 $a + \sqrt{1 - 2 a + a^{2}}$ 的值”时谁的答案正确，并说明理由．
甲的答案：原式 $= a + \sqrt{{(1 - a)}^{2}} = a + (1 - a) = 1$ ；
乙的答案：原式 $= a + \sqrt{{(1 - a)}^{2}} = a + (a - 1) = 2 a - 1 = 2 \times 9 - 1 = 17$ ．

(3)、化简并求值： $| x - 1 | + \sqrt{4 - 4 x + x^{2}}$ ，其中 $x = \sqrt{5}$ ．

查看试题解析