2023年中考数学精选真题实战测试9 二次根式A

试卷更新日期：2023-01-04 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在函数y＝ $\frac{\sqrt{x + 3}}{x}$ 中，自变量x的取值范围是（）

A、x≥3 B、x≥﹣3 C、x≥3且x≠0 D、x≥﹣3且x≠0

查看试题解析
2. 估计 $(2 \sqrt{5} + 5 \sqrt{2}) \times \sqrt{\frac{1}{5}}$ 的值应在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
3. 下列说法正确的是（）
①若二次根式 $\sqrt{1 - x}$ 有意义，则x的取值范围是x≥1．
②7＜ $\sqrt{65}$ ＜8．
③若一个多边形的内角和是540°，则它的边数是5．
④ $\sqrt{16}$ 的平方根是±4．
⑤一元二次方程x²﹣x﹣4＝0有两个不相等的实数根．

A、①③⑤ B、③⑤ C、③④⑤ D、①②④

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt[2]{- 8} = 2$ B、 $\sqrt{(- 3)^{2}} = - 3$ C、 $2 \sqrt{5} + 3 \sqrt{5} = 5 \sqrt{5}$ D、 $(\sqrt{2} + 1)^{2} = 3$

查看试题解析
5. 下列正确的是（）

A、 $\sqrt{4 + 9} = 2 + 3$ B、 $\sqrt{4 \times 9} = 2 \times 3$ C、 $\sqrt{9^{4}} = \sqrt{3^{2}}$ D、 $\sqrt{4.9} = 0.7$

查看试题解析
6. 下列各组二次根式中，化简后是同类二次根式的是（）

A、 $\sqrt{8}$ 与 $\sqrt{3}$ B、 $\sqrt{2}$ 与 $\sqrt{12}$ C、 $\sqrt{5}$ 与 $\sqrt{15}$ D、 $\sqrt{75}$ 与 $\sqrt{27}$

查看试题解析
7. 下列等式成立的是（）

A、 $3 + 4 \sqrt{2} = 7 \sqrt{2}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{5}$ C、 $\sqrt{3} \div \frac{1}{\sqrt{6}} = 2 \sqrt{3}$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
8. 计算 $\sqrt{12} - \sqrt{12} \times \sqrt{\frac{1}{4}}$ 的结果是（）

A、0 B、 $\sqrt{3}$ C、 $3 \sqrt{3}$ D、 $\frac{1}{2}$

查看试题解析
9. $2 ， 5 ， m$ 是某三角形三边的长，则 $\sqrt{{(m - 3)}^{2}} + \sqrt{{(m - 7)}^{2}}$ 等于（）

A、 $2 m - 10$ B、 $10 - 2 m$ C、10 D、4

查看试题解析
10. 已知实数a在数轴上的对应点位置如图所示，则化简 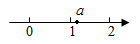$| a - 1 | - \sqrt{{(a - 2)}^{2}}$ 的结果是（）

A、 $3 - 2 a$ B、-1 C、1 D、 $2 a - 3$

查看试题解析

二、填空题（每空3分，共18分）

11. 若（a﹣3）²+ $\sqrt{b - 5}$ =0，则以a、b为边长的等腰三角形的周长为.

查看试题解析
12. 若实数m，n满足 $∣ m - n - 5 ∣ + \sqrt{2 m + n - 4} = 0$ ，则 $3 m + n =$ .

查看试题解析
13. 若 $3 - \sqrt{2}$ 的整数部分为a，小数部分为b，则代数式 $(2 + \sqrt{2} a) \cdot b$ 的值是.

查看试题解析
14. 实数a、b在数轴上的位置如图所示，化简|a+1|﹣ $\sqrt{{(b - 1)}^{2}} + \sqrt{{(a - b)}^{2}}$ ＝.

查看试题解析
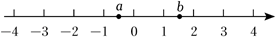15. 人们把 $\frac{\sqrt{5} - 1}{2}$ 这个数叫做黄金分割数，著名数学家华罗庚优选法中的 $0.618$ 法就应用了黄金分割数.设 $a = \frac{\sqrt{5} - 1}{2}$ ， $b = \frac{\sqrt{5} + 1}{2}$ ，则 $a b = 1$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $S_{2} = \frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ ，…， $S_{10} = \frac{1}{1 + a^{10}} + \frac{1}{1 + b^{10}}$ .则 $S_{1} + S_{2} + \dots + S_{10} =$ .

查看试题解析
16. 对于任意不相等的两个实数a，b（ a > b ）定义一种新运算a※b= $\frac{\sqrt{a + b}}{\sqrt{a - b}}$ ，如3※2= $\frac{\sqrt{3 + 2}}{\sqrt{3 - 2}}$ ，那么12※4=

查看试题解析

三、解答题（共9题，共72分）

17. 计算： $\sqrt{12} + | \sqrt{3} - 3 | - {(\frac{1}{3})}^{- 1}$ .

查看试题解析
18. 计算： ${(- 3)}^{2} + 2 \times (\sqrt{2} - 1) - | - 2 \sqrt{2} |$

查看试题解析
19. 计算 $| - \sqrt{2} | + {(\sqrt{2} - \frac{1}{2})}^{2} - {(\sqrt{2} + \frac{1}{2})}^{2}$ ．

查看试题解析
20. 计算： ${(\sqrt{2021} - π)}^{0} + \frac{1}{\sqrt{2} + 1} + {(\frac{1}{2})}^{- 1} - 2 \cos 45 °$ .

查看试题解析
21. 如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示 $- \sqrt{2}$ ，设点B所表示的数为m．

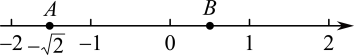(1)、求 $| m + 1 | + | m - 1 |$ 的值；

(2)、在数轴上还有C、D两点分别表示实数c和d，且有|2c＋6|与 $\sqrt{d - 4}$ 互为相反数，求2c+3d 的平方根．

查看试题解析
22. 观察下列等式：
第1个等式：a₁= $\frac{1}{1 + \sqrt{2}}$ = $\sqrt{2}$ ﹣1，
第2个等式：a₂= $\frac{1}{\sqrt{2} + \sqrt{3}}$ = $\sqrt{3}$ ﹣ $\sqrt{2}$ ，
第3个等式：a₃= $\frac{1}{\sqrt{3} + 2}$ =2﹣ $\sqrt{3}$ ，
第4个等式：a₄= $\frac{1}{2 + \sqrt{5}}$ = $\sqrt{5}$ ﹣2，
按上述规律，回答以下问题：

(1)、请写出第n个等式：a_n=；

(2)、a₁+a₂+a₃+…+a_n= ．

查看试题解析
23. 阅读下面的材料，解答后面所给出的问题：两个含二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式互为有理化因式．例如： $\sqrt{a}$ 与 $\sqrt{a}$ ， $\sqrt{2} + 1$ 与 $\sqrt{2} - 1$ ．

(1)、请你写出两个二次根式，使它们互为有理化因式：，这样化简一个分母含有二次根式的式子时，采用分母、分子同乘分母的有理化因式的方法就可以了．例如： $\frac{\sqrt{2}}{\sqrt{3} - \sqrt{2}} = \frac{\sqrt{2} (\sqrt{3} + \sqrt{2})}{(\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2})} = \frac{\sqrt{6} + 2}{3 - 2} = \sqrt{6} + 2$ ．

(2)、请仿照上述方法化简： $\frac{3}{\sqrt{5} - \sqrt{2}}$ ；

(3)、比较 $\frac{1}{\sqrt{3} - 1}$ 与 $\frac{1}{\sqrt{5} - \sqrt{3}}$ 的大小．

查看试题解析
24. 先观察下列的计算，再完成练习．
（1） $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
（2） $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
（3） $\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．
请你分析、归纳上面的解题方式，解决如下问题：

(1)、化简： $\frac{1}{\sqrt{5} + \sqrt{4}}$ ；

(2)、已知n是正整数，求 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ 的值：

(3)、计算： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2023} + \sqrt{2022}}) \times (\sqrt{2023} + 1)$ ．

查看试题解析
25. 阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2 $\sqrt{2}$ ＝（1+ $\sqrt{2}$ ）² ．善于思考的小明进行了以下探索：
设a+b $\sqrt{2}$ ＝（m+n $\sqrt{2}$ ）²（其中a、b、m、n均为整数），则有a+b $\sqrt{2}$ ＝m²+2n²+2 $\sqrt{2}$ mn．∴a＝m²+2n² ， b＝2mn．这样小明就找到了一种把类似a+b $\sqrt{2}$ 的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：

(1)、当a、b、m、n均为正整数时，若a+b $\sqrt{3}$ ＝（m+n $\sqrt{3}$ ）² ，用含m、n的式子分别表示a、b，得：a＝， b＝；

(2)、利用所探索的结论，找一组正整数a、b、m、n填空：+ $\sqrt{3}$ ＝（+ $\sqrt{3}$ ）²；

(3)、若a+6 $\sqrt{3}$ ＝（m+n $\sqrt{3}$ ）² ，且a、m、n均为正整数，求a的值？

查看试题解析