甘肃省定西市安定区2022-2023学年八年级上学期期中数学试题
试卷更新日期:2023-01-04 类型:期中考试
一、单选题
-
1. “致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,常被用于建筑、器物、绘画、标识等作品的设计上,使对称美惊艳了千年的时光.下列大学的校徽图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列四组图形中,是全等形的一组是( )A、
2. 下列四组图形中,是全等形的一组是( )A、 B、
B、 C、
C、 D、
D、 3. 下列选项中的三条线段能首尾相接构成三角形的是( )A、1cm,2cm,4cm B、3cm,4cm,8cm C、9cm,6cm,4cm D、5cm,5cm,10cm4. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )
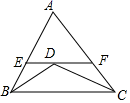
3. 下列选项中的三条线段能首尾相接构成三角形的是( )A、1cm,2cm,4cm B、3cm,4cm,8cm C、9cm,6cm,4cm D、5cm,5cm,10cm4. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )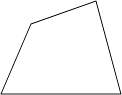 A、0根 B、1根 C、2根 D、3根5. 点P(-3,1)关于y轴对称点的坐标为( )A、(1,-3) B、(3,1) C、(-3,-1) D、(3, -1)6. 如图,是的中线,已知的周长为25cm,比长7cm,则的周长( )
A、0根 B、1根 C、2根 D、3根5. 点P(-3,1)关于y轴对称点的坐标为( )A、(1,-3) B、(3,1) C、(-3,-1) D、(3, -1)6. 如图,是的中线,已知的周长为25cm,比长7cm,则的周长( )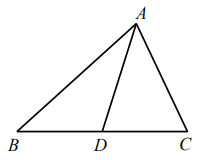 A、18cm B、22cm C、19cm D、31cm7. 如图,在中, , , 平分 , 于点E,则的度数为( )
A、18cm B、22cm C、19cm D、31cm7. 如图,在中, , , 平分 , 于点E,则的度数为( )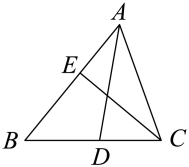 A、 B、 C、 D、8. 如图,已知 , 线段与交于点O,则下面的结论中不正确的是( )
A、 B、 C、 D、8. 如图,已知 , 线段与交于点O,则下面的结论中不正确的是( )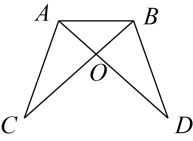 A、 B、 C、 D、9. 如图,△ABC中,AD平分∠BAC,AB=4,AC=2,若△ACD的面积等于3,则△ABD的面积为( )
A、 B、 C、 D、9. 如图,△ABC中,AD平分∠BAC,AB=4,AC=2,若△ACD的面积等于3,则△ABD的面积为( )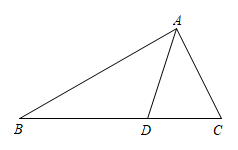 A、8 B、4 C、6 D、1210. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC-AB=2BE中,正确的是( )
A、8 B、4 C、6 D、1210. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC-AB=2BE中,正确的是( )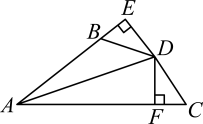 A、①②③ B、①②③④ C、①②④ D、②③④
A、①②③ B、①②③④ C、①②④ D、②③④二、填空题
-
11. 已知a,b,c是的三边长,a,b满足 , c为奇数,则c=.12. 如图,CE是的外角∠ACD的平分线,若 , , 则∠A=.
 13. 如图,已知平分 , 要使 , 需要添加的条件是(添加一个即可).
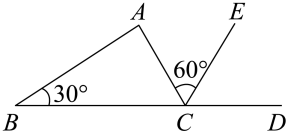
13. 如图,已知平分 , 要使 , 需要添加的条件是(添加一个即可).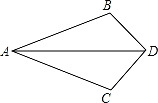 14. 如图,直线的顶点B、C分别在直线n、m上,且 , 若 , 则的度数为.
14. 如图,直线的顶点B、C分别在直线n、m上,且 , 若 , 则的度数为.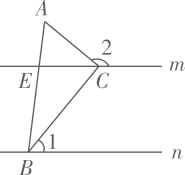 15. 如图,在△ABC和△ADE中,∠BAC =∠DAE=90°,∠B=50°,∠E=65°,则①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=40°,则有BC∥AD;④如果∠2=30°,则有AC∥DE,上述结论中正确的是 .(填写序号)
15. 如图,在△ABC和△ADE中,∠BAC =∠DAE=90°,∠B=50°,∠E=65°,则①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=40°,则有BC∥AD;④如果∠2=30°,则有AC∥DE,上述结论中正确的是 .(填写序号)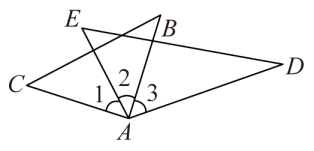 16. 如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是 .
16. 如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是 .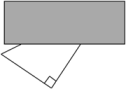 17. 如图,是的角平分线, , 垂足为E, , , , 则长是.
17. 如图,是的角平分线, , 垂足为E, , , , 则长是.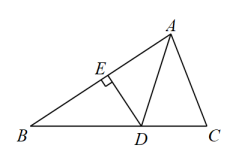 18. 如图,点O是 的两外角平分线的交点,下列结论:①;②点O到AB、AC的距离相等;③点O到的三边的距离相等;④点O在的平分线上.其中结论正确的是(填序号).
18. 如图,点O是 的两外角平分线的交点,下列结论:①;②点O到AB、AC的距离相等;③点O到的三边的距离相等;④点O在的平分线上.其中结论正确的是(填序号).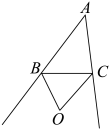
三、解答题
-
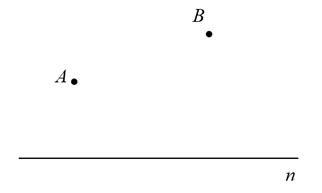
19. 在图中直线n上作出点C,使的值最小.(不写作法,保留作图痕迹)
 20. 回答下列问题:(1)、一个等腰三角形的周长是 , 若它的一条边长为 , 求它的另两条边长.(2)、一个等腰三角形的一边长是4,另一边长是9,求这个等腰三角形的周长.21. 如图,已知点C,F在直线AD上,且有BC=EF,AB=DE,CD=AF.求证:∆ABC≌∆DEF.
20. 回答下列问题:(1)、一个等腰三角形的周长是 , 若它的一条边长为 , 求它的另两条边长.(2)、一个等腰三角形的一边长是4,另一边长是9,求这个等腰三角形的周长.21. 如图,已知点C,F在直线AD上,且有BC=EF,AB=DE,CD=AF.求证:∆ABC≌∆DEF.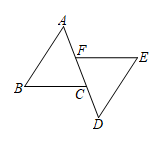 22. 如图,在平面直角坐标系中,△ABC的顶点都在网格线的交点上,点B的坐标为 , 点C的坐标为 .
22. 如图,在平面直角坐标系中,△ABC的顶点都在网格线的交点上,点B的坐标为 , 点C的坐标为 .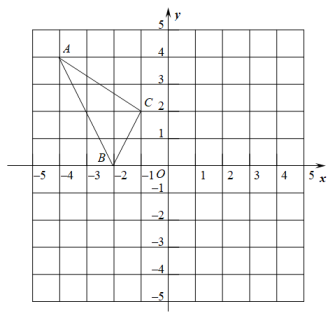 (1)、直接写出点A的坐标和点A关于y轴的对称点的坐标,并画出关于y轴的对称图形;(不写画法,保留画图痕迹)(2)、求的面积.23. 如图,中,D,E分别是边延长线上的点,平分 , 平分 , 求证:平分.
(1)、直接写出点A的坐标和点A关于y轴的对称点的坐标,并画出关于y轴的对称图形;(不写画法,保留画图痕迹)(2)、求的面积.23. 如图,中,D,E分别是边延长线上的点,平分 , 平分 , 求证:平分.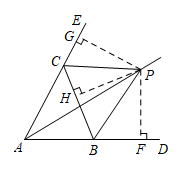
证:过P分别作 ,
∵平分( ),
且 ,
∴ ▲ .(角平分线上的点到角的两边的距离相等)
∵平分
且 ▲ ,
∴ ,
∴ ▲ .( )
又∵ ,
∴平分.
24. 如图,在四边形中, , 分别是及的平分线.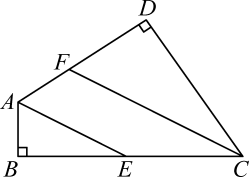 (1)、求证:;(2)、若 , 求.
(1)、求证:;(2)、若 , 求.