浙教版备考2023年中考数学一轮复习47.直线的相交于平行
试卷更新日期:2023-01-03 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
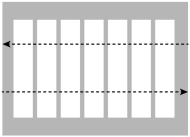 A、垂线段最短 B、两点确定一条直线 C、过一点有且只有一条直线与已知直线垂直 D、过直线外一点有且只有一条直线与已知直线平行2. 过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )A、
A、垂线段最短 B、两点确定一条直线 C、过一点有且只有一条直线与已知直线垂直 D、过直线外一点有且只有一条直线与已知直线平行2. 过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
3. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )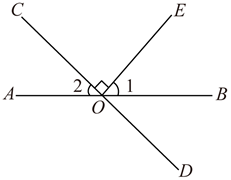 A、26° B、36° C、44° D、54°4. 如图,直线 , , ,则 ( )
A、26° B、36° C、44° D、54°4. 如图,直线 , , ,则 ( ) A、 B、 C、 D、5. 如图,直线 相交于点 ;若 ,则 的度数是( )
A、 B、 C、 D、5. 如图,直线 相交于点 ;若 ,则 的度数是( ) A、30° B、40° C、60° D、150°6. 当光线从空气中射入某种液体中时,光线的传播方向发生了变化,在物理学中这种现象叫做光的折射.如图,液面MN于点D,一束光线沿CD射入液面,在点D处发生折射,折射光线为DE,点F为CD的延长线上一点,若入射角 , 折射角 , 则的度数为( )
A、30° B、40° C、60° D、150°6. 当光线从空气中射入某种液体中时,光线的传播方向发生了变化,在物理学中这种现象叫做光的折射.如图,液面MN于点D,一束光线沿CD射入液面,在点D处发生折射,折射光线为DE,点F为CD的延长线上一点,若入射角 , 折射角 , 则的度数为( ) A、14° B、16° C、18° D、25°7. 如图,在中, , , , 则射线 与 ( )
A、14° B、16° C、18° D、25°7. 如图,在中, , , , 则射线 与 ( ) A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交8. 如图,把长方形沿对折后使两部分重合,若 , 则( )
A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交8. 如图,把长方形沿对折后使两部分重合,若 , 则( ) A、 B、 C、 D、9. 如图, , , 平分 , 平分 , 则( )
A、 B、 C、 D、9. 如图, , , 平分 , 平分 , 则( )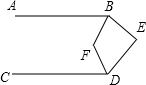 A、 B、 C、 D、10. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )
A、 B、 C、 D、10. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )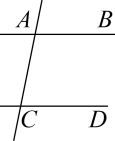 A、③④ B、①③④ C、①②④ D、②③④
A、③④ B、①③④ C、①②④ D、②③④二、填空题
-
11. a、b、c是直线,且a∥b,b⊥c,则a与c的位置关系是 .12. 在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,∠BAC=90°,在△ABC的面积是.
 13. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 .
13. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 . 14. 两个三角形如图摆放,其中∠BAC=90°,∠EDF=100°,∠B=60°,∠F=40°,DE与AC交于M,若 , 则∠DMC的大小为 .
14. 两个三角形如图摆放,其中∠BAC=90°,∠EDF=100°,∠B=60°,∠F=40°,DE与AC交于M,若 , 则∠DMC的大小为 .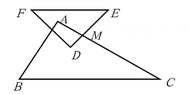 15. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 .
15. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 . 16. 如图,直线l1 , l2 , l3被直线l4所截,若l1l2 , l2l3 , ∠1=126°32',则∠2的度数是 .
16. 如图,直线l1 , l2 , l3被直线l4所截,若l1l2 , l2l3 , ∠1=126°32',则∠2的度数是 .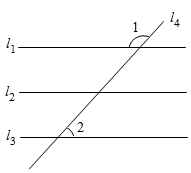
三、解答题(共8题,共66分)
-
17. 如图,在4×4的方格纸中,点A,B在格点上.请按要求画出格点线段(线段的端点在格点上),并写出结论.
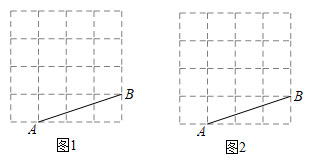 (1)、在图1中画一条线段垂直AB.(2)、在图2中画一条线段平分AB.18. 如图,AB,CD交于点O,OA⊥OE,OF平分∠BOC,∠COF=68°.求∠DOE的度数.
(1)、在图1中画一条线段垂直AB.(2)、在图2中画一条线段平分AB.18. 如图,AB,CD交于点O,OA⊥OE,OF平分∠BOC,∠COF=68°.求∠DOE的度数. 19. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.
19. 下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线 , 与的面积相等吗?为什么?
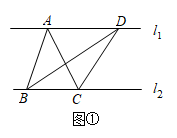
解:相等.理由如下:
设与之间的距离为 , 则 , .
∴ .
【探究】
(1)、如图②,当点在 , 之间时,设点 , 到直线的距离分别为 , , 则 .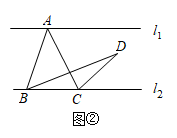
证明:∵ ▲
▲
▲
(2)、如图③,当点在 , 之间时,连接并延长交于点 , 则 .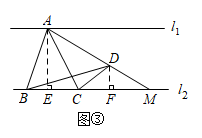
证明:过点作 , 垂足为 , 过点作 , 垂足为 , 则 ,
∴ ▲ .
∴ ▲ .
∴ .
由【探究】(1)可知 ▲ ,
∴ .
(3)、如图④,当点在下方时,连接交于点 . 若点 , , 所对应的刻度值分别为5,1.5,0,的值为 .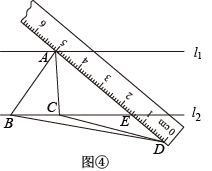 20. 如图,在中,分别平分 , 交于点.
20. 如图,在中,分别平分 , 交于点.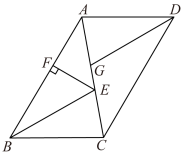 (1)、求证:;(2)、过点作 , 垂足为.若的周长为56, , 求的面积.21. 如图
(1)、求证:;(2)、过点作 , 垂足为.若的周长为56, , 求的面积.21. 如图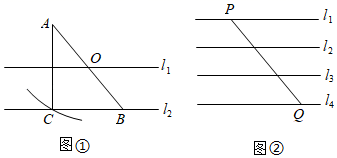 (1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)22. 小明完成暑假作业后在家复习,他看到七下课本12页例4:“如图1﹣13,AP平分∠BAC,CP平分∠ACD,∠1+∠2=90°.判断AB,CD是否平行,并说明理由.”,试着“玩”起数学来:
(1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)22. 小明完成暑假作业后在家复习,他看到七下课本12页例4:“如图1﹣13,AP平分∠BAC,CP平分∠ACD,∠1+∠2=90°.判断AB,CD是否平行,并说明理由.”,试着“玩”起数学来: (1)、【基础巩固】
(1)、【基础巩固】
条件和结论互换,改成了:“如图1﹣13,AP平分∠BAC,CP平分∠ACD,AB∥CD,则∠1+∠2=90°.”小明认为这个结论正确.你赞同他的想法吗?请说明理由.(2)、【尝试探究】
小明发现:若将其中一条角平分线改成AC的垂线,则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究:如图1,AB∥CD,AP平分∠BAC,CP⊥AC,∠1是AP与AB的夹角,∠2是CP与CD的夹角,
①若∠2=22°,求∠1的度数;
②试说明:2∠1﹣∠2=90°.
(3)、【拓展提高】
如图2,若AB∥CD,AP⊥AC,CP平分∠ACD,请直接写出∠1与∠2的等量关系.23. 在综合与实践课上,老师与同学们以“两条平行线和一块含角的直角三角尺”为主题开展数学活动. (1)、如图(1),若三角尺的角的顶点放在上,若 , 求的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点分别放在和上,请你探索并说明与间的数量关系;(3)、如图(3),小亮把三角尺的直角顶点放在上,角的顶点落在上.若 , 则与的数量关系是什么?用含的式子表示.24. 如图①, , 点A,C分别在射线FE和FH上, .
(1)、如图(1),若三角尺的角的顶点放在上,若 , 求的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点分别放在和上,请你探索并说明与间的数量关系;(3)、如图(3),小亮把三角尺的直角顶点放在上,角的顶点落在上.若 , 则与的数量关系是什么?用含的式子表示.24. 如图①, , 点A,C分别在射线FE和FH上, .
 (1)、若 , 则的度数为;(2)、小明同学发现,无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图②,过点A作 , 交CD于点M.请你根据小明同学提供的辅助线,确定该定值,并说明理由;(3)、如图③,把“”改为“”,其他条件保持不变,猜想与的数量关系,并说明理由.
(1)、若 , 则的度数为;(2)、小明同学发现,无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图②,过点A作 , 交CD于点M.请你根据小明同学提供的辅助线,确定该定值,并说明理由;(3)、如图③,把“”改为“”,其他条件保持不变,猜想与的数量关系,并说明理由.